
Конспект урока "Векторная алгебра"
Глава 1. Векторная алгебра
В этой главе мы приведем сведения о геометрических векторах и операциях над ними, включая векторное произведение двух векторов и смешанное произведение трех векторов.
§1.1. Основные определения.
1.1.1. Определение. Вектором называется направленный отрезок или упорядоченная пара точек. Начало вектора также называется точкой его приложения.
Замечание.
Упорядоченным множеством называется множество элементов, взятых в определенном порядке. Обозначать векторы принято одним из следующих способов: ![]() (А – начальная точка, В – конечная точка),
(А – начальная точка, В – конечная точка), ![]() ,
,![]() , и т.д. Чтобы отличить векторную величину от скалярной величины, сверху используется черта (или стрелочка). Скалярной называется величина, характеризующаяся только своим численным значением (примеры: объем, температура, масса и т.д.). Для описания других объектов необходимо задавать не только их численное значение, но и направление (сила, скорость и т.д.); такие объекты называются векторными величинами.
, и т.д. Чтобы отличить векторную величину от скалярной величины, сверху используется черта (или стрелочка). Скалярной называется величина, характеризующаяся только своим численным значением (примеры: объем, температура, масса и т.д.). Для описания других объектов необходимо задавать не только их численное значение, но и направление (сила, скорость и т.д.); такие объекты называются векторными величинами.
1.1.2. Определение. Нулевым вектором или нуль-вектором называется вектор, начало и конец которого совпадают.
Замечание.
Направление нулевого вектора не определяется (считается произвольным). Нуль-вектор будем обозначать ![]() .
.
1.1.3. Определение. Длиной (модулем, абсолютной величиной) вектора называется расстояние между его началом и его концом. Обозначение: 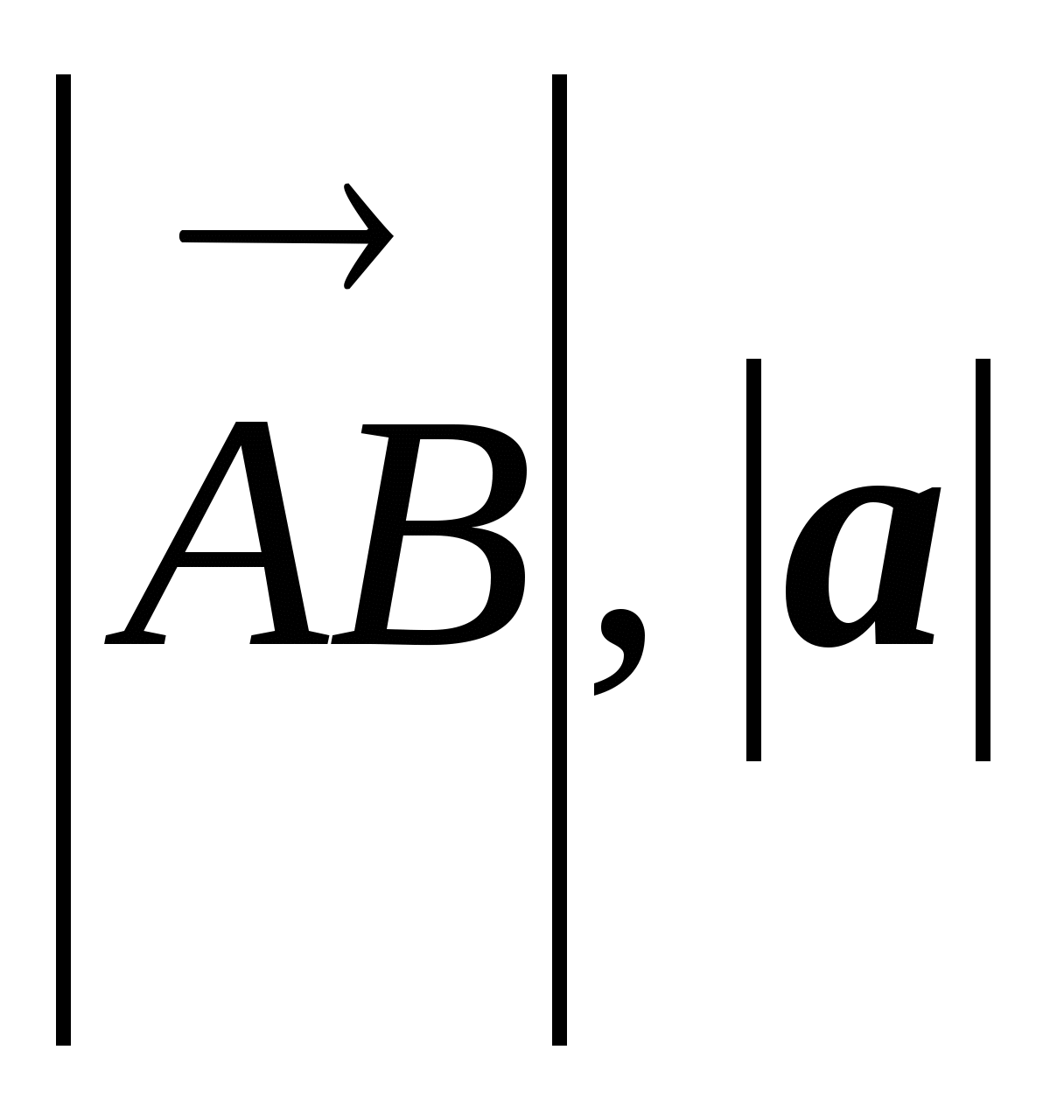 . Естественно,
. Естественно, ![]() .
.
1.1.4. Определение. Векторы называются коллинеарными, если они расположены на одной или на параллельных прямых. Иными словами, векторы коллинеарны, если существует прямая, которой они параллельны. Коллинеарность обозначается символом параллельности: ![]() . Нуль-вектор коллинеарен любому другому вектору, так как он не имеет определенного направления:
. Нуль-вектор коллинеарен любому другому вектору, так как он не имеет определенного направления: ![]() .
.
Ненулевые коллинеарные вектора, могут быть
(a) сонаправленными (имеющими одинаковое направление), что мы будем обозначать ![]() ;
;
(б) противонаправленными (имеющими противоположное направление), что мы будем обозначать ![]() .
.
Замечание.
Отметим очевидные свойства отношений сонаправленности и противонаправленности:
1. Если ![]() ,
,![]() , то
, то ![]() ;
;
2. Если ![]() ,
,![]() , то
, то ![]() ;
;
3. Если ![]() ,
,![]() , то
, то ![]() ;
;
4. Если ![]() ,
,![]() , то
, то ![]() .
.
1.1.5. Определение. Векторы называются компланарными, если существует плоскость, которой они параллельны.
1.1.6. Определение. Два вектора называются равными, если они коллинеарны, сонаправлены и имеют равные длины.
Замечание 1.
Все нулевые векторы равны между собой.
Замечание 2.
Введем понятия связанного, скользящего и свободных векторов. Связанным называется вектор, имеющий фиксированное начало и конец. Скользящим вектором называется множество всех связанных векторов, равных данному, начала которых расположены на одной и той же прямой. Свободным вектором называется множество всех связанных векторов, равных данному. Таким образом, скользящий вектор может быть перенесен вдоль прямой, на которой он лежит, а свободный вектор может быть отложен из любой заданной точки. Понятие свободного вектора является наиболее общим, так как любой связанный или скользящий вектор может быть представлен в виде разности двух свободных векторов.
1.1.7. Определение. Ортом, или единичным вектором, называется вектор, длина которого равна единице.
1.1.8. Определение. Ортом вектора ![]() называется единичный вектор, сонаправленный с вектором
называется единичный вектор, сонаправленный с вектором ![]() . Орт вектора
. Орт вектора ![]() будем обозначать
будем обозначать ![]() .
.
1.1.9. Определение. Углом между ненулевыми векторами называется угол между прямыми, на которых расположены данные векторы.
1.1.10. Определение. Векторы, лежащие на перпендикулярных прямых, называются ортогональными.
1.1.11. Определение. Вектор, имеющий одинаковый модуль с вектором ![]() и противонаправленный ему, будем называть противоположным вектору
и противонаправленный ему, будем называть противоположным вектору ![]() и обозначать
и обозначать ![]() . Если
. Если ![]() , то
, то ![]() .
.
§1.2. Линейные операции над векторами.
1.2.1. Определение. Линейными операциями над векторами назовем операции сложения двух векторов и умножения вектора на скаляр (число).

1.2.2. Определение. Суммой ![]() двух векторов
двух векторов ![]() и
и ![]() назовем вектор, идущий из начала вектора
назовем вектор, идущий из начала вектора ![]() в конец вектора
в конец вектора ![]() .
.
1.2.3. Правила сложения векторов.
а ) Правило треугольника (Рис. 1.1)
) Правило треугольника (Рис. 1.1)
Вектор ![]() прикладывается к концу вектора
прикладывается к концу вектора ![]() . Тогда сумма векторов
. Тогда сумма векторов ![]() будет вектор, идущий из начала вектора
будет вектор, идущий из начала вектора ![]() в конец вектора
в конец вектора ![]() .
.
б) Правило параллелограмма (Рис. 1.2)
С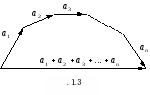 троим на векторах
троим на векторах ![]() и
и ![]() параллелограмм. Тогда суммой векторов
параллелограмм. Тогда суммой векторов ![]() будет диагональ параллелограмма, выходящая из общего начала векторов
будет диагональ параллелограмма, выходящая из общего начала векторов ![]() и
и ![]() .
.
Замечание.
П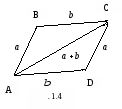 равило треугольника легко распространить на случай большего количества суммируемых векторов. В этом случае это правило называется правилом многоугольника (Рис. 1.3 ).
равило треугольника легко распространить на случай большего количества суммируемых векторов. В этом случае это правило называется правилом многоугольника (Рис. 1.3 ).
Обозначим множество свободных векторов через ![]() .
.
1.2.4. Теорема. (Свойства операции сложения векторов)
1. ![]()
![]()
![]() ,
,![]() (коммутативность);
(коммутативность);
2. ![]()
![]() (ассоциативность);
(ассоциативность);
3. ![]()
![]() ;
;
4. ![]() .
.
Доказательство:
1. Рассмотрим сумму векторов ![]() и
и ![]() , используя правило параллелограмма. Из Рис. 1.4
, используя правило параллелограмма. Из Рис. 1.4
![]()
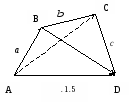
2. Из Рис. 1.5.
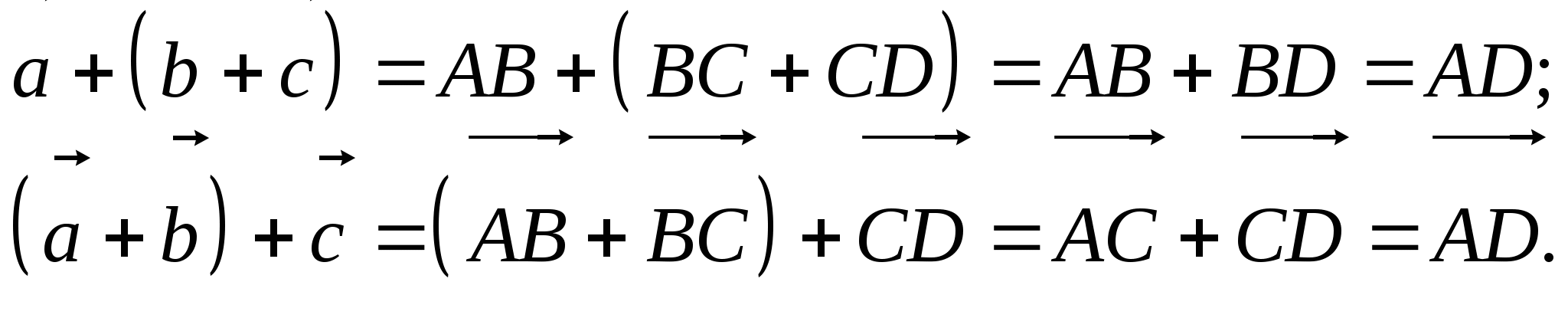
3. Третье свойство очевидно: ![]()
4. Пусть ![]() Положим
Положим ![]() Тогда
Тогда ![]()
1.2.5. Определение. Разностью ![]() двух векторов
двух векторов ![]() и
и ![]() назовем вектор
назовем вектор ![]() , для которого
, для которого
![]() .
.
1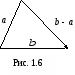 .2.6. Правило вычитания векторов.
.2.6. Правило вычитания векторов.
Разностью векторов ![]() двух векторов
двух векторов ![]() и
и ![]() является вектор
является вектор ![]() , идущий из конца второго вектора
, идущий из конца второго вектора ![]() в конец первого вектора
в конец первого вектора ![]() (Рис. 1.6).
(Рис. 1.6).
Замечание.
Очевидно, что ![]() .
.
1.2.7. Определение. Произведением вектора ![]() на действительное число
на действительное число ![]() называется вектор
называется вектор ![]() , удовлетворяющий следующим условиям:
, удовлетворяющий следующим условиям:
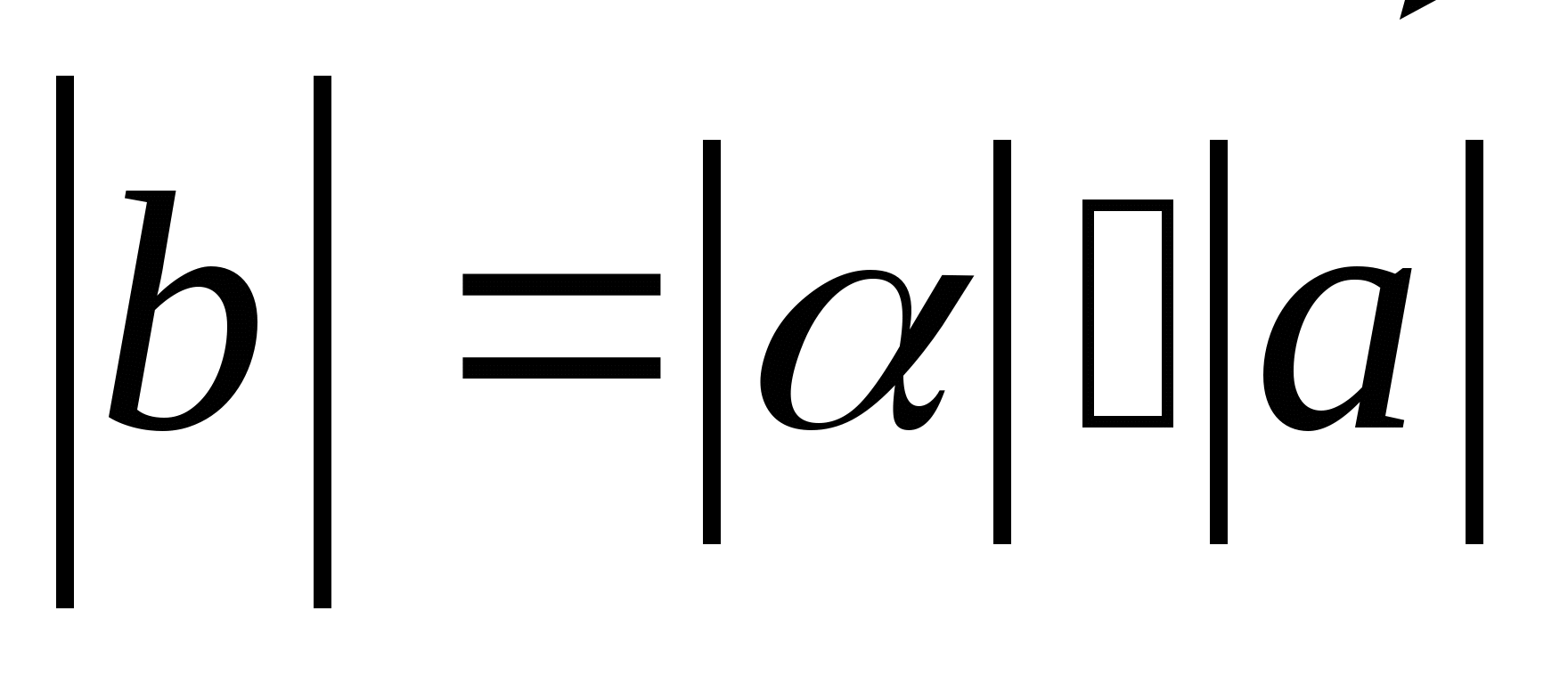 ;
;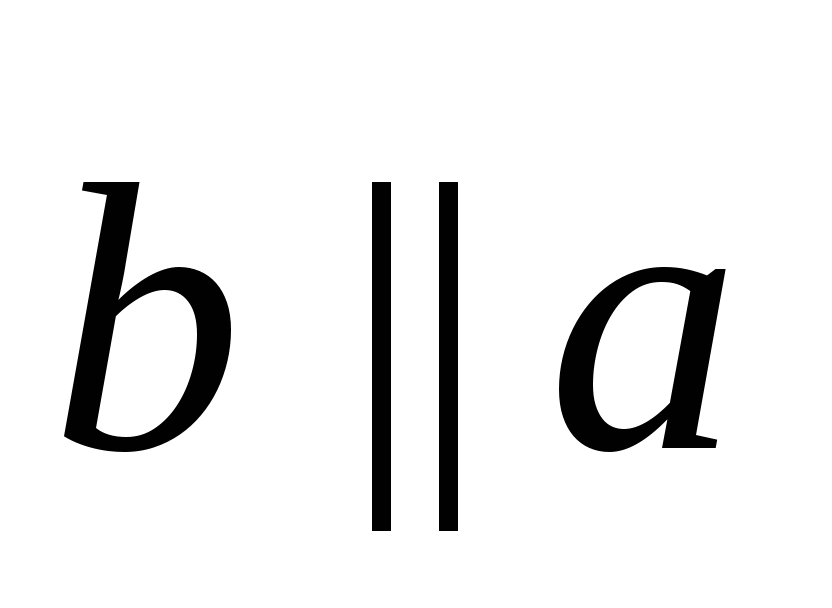 ;
;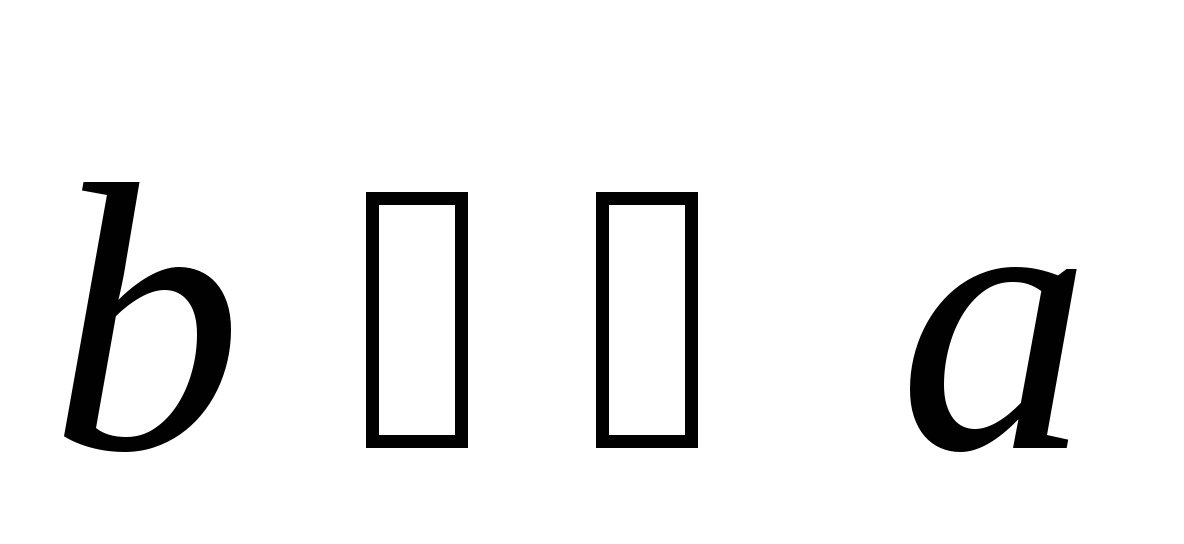 при
при 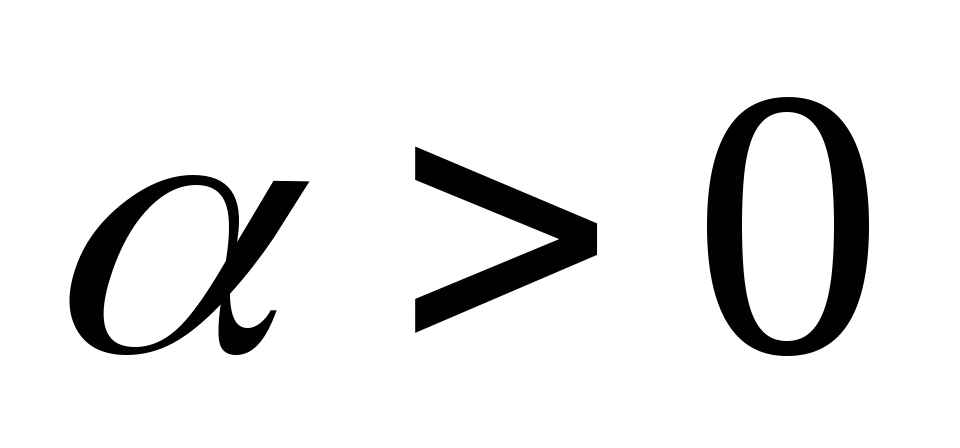 и
и  при
при  .
.
1.2.8. Теорема. (Критерий коллинеарности двух векторов).
Для того, чтобы два вектора ![]() и
и ![]() были коллинеарны, необходимо и достаточно, чтобы существовало действительное число
были коллинеарны, необходимо и достаточно, чтобы существовало действительное число ![]() , что
, что ![]() .
.
Доказательство:
Необходимость.
Пусть ![]() . Рассмотрим вектор
. Рассмотрим вектор ![]() , где число
, где число ![]() выберем следующим образом: если
выберем следующим образом: если ![]() , то
, то ![]() ; если
; если ![]() , то
, то 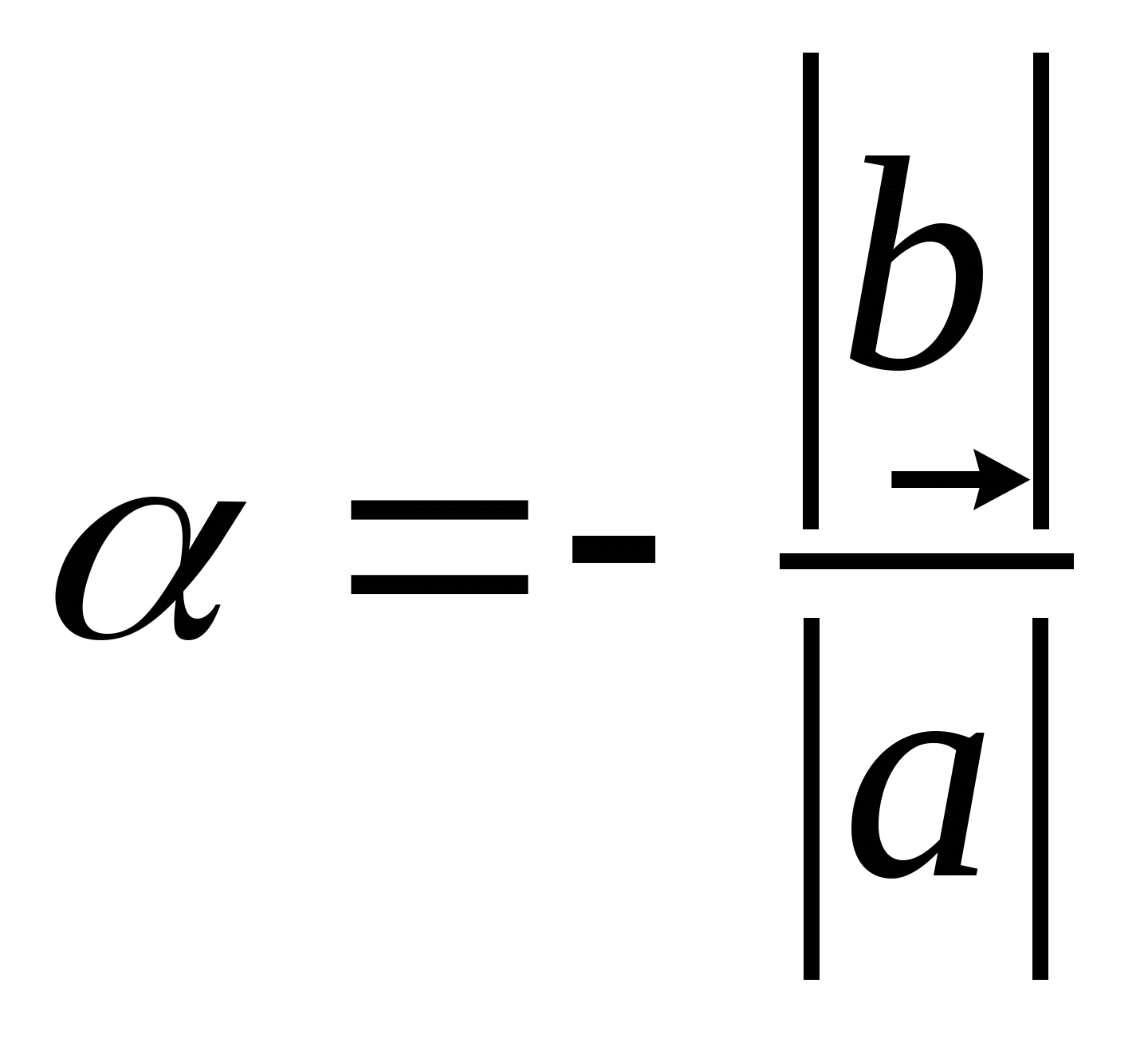 . Очевидно,
. Очевидно, ![]() , так как
, так как ![]() и
и ![]() . Таким образом, мы указали число
. Таким образом, мы указали число ![]() , для которого
, для которого ![]() .
.
Достаточность.
Если ![]() , то из определения 1.2.7, очевидно, вытекает коллинеарность векторов
, то из определения 1.2.7, очевидно, вытекает коллинеарность векторов ![]() и
и ![]() .
.
1.2.9. Теорема. (Свойства операции умножения вектора на число)
1. ![]() (ассоциативность);
(ассоциативность);
2. ![]() (дистрибутивность относительно суммы скаляров);
(дистрибутивность относительно суммы скаляров);
3. ![]() (дистрибутивность относительно суммы векторов);
(дистрибутивность относительно суммы векторов);
4. ![]()
![]() ;
;
5. ![]()
![]() ;
;
6. ![]()
![]() ;
;
7. ![]() .
.
Доказательство этих свойств очевидно, читатели могут легко проделать его самостоятельно.
1.2.10. Определение. Делением вектора ![]() на действительное число
на действительное число ![]() называется его умножение на число
называется его умножение на число ![]() .
.
Замечание.
Отметим, что орт вектора ![]()
§1.3. Ортогональная проекция вектора на направление.
1.3.1. Определение. Осью будем называть прямую, на которой заданы начало отсчета, масштаб (единица длины) и положительное направление.
1 .3.2. Определение. Ортогональной проекцией вектора
.3.2. Определение. Ортогональной проекцией вектора ![]() на направление (ось) l называется число, равное длине отрезка A1B1, где A1 и B1 основания перпендикуляров, опущенных из концов вектора
на направление (ось) l называется число, равное длине отрезка A1B1, где A1 и B1 основания перпендикуляров, опущенных из концов вектора ![]() на направление l, взятое со знаком плюс, если направление вектора
на направление l, взятое со знаком плюс, если направление вектора ![]() совпадает с направлением l и со знаком минус, если направление вектора
совпадает с направлением l и со знаком минус, если направление вектора ![]() противоположно направлению l.
противоположно направлению l.
Замечание.
Проекция вектора ![]() на направление l будем обозначать
на направление l будем обозначать ![]() . Например, на Рис. 1.7
. Например, на Рис. 1.7 ![]() ,
, ![]() .
.
1.3.3. Свойства ортогональной проекции вектора на направление.
1.3.3.1. Теорема. (Свойство 1)
Проекция вектора на направление равна произведению его длины на косинус угла между вектором и положительным направлением оси:
![]() , где
, где ![]() .
.
1.3.3.2. Теорема. (Свойство 2)
Проекция суммы векторов на направление l равна сумме проекций слагаемых на это направление:
![]() .
.
1.3.3.3. Теорема. (Свойство 3)
Проекция произведения вектора ![]() на число на направление l равна произведению этого числа на проекцию вектора
на число на направление l равна произведению этого числа на проекцию вектора ![]() на это направление:
на это направление:
![]() .
.
Докажите эти теоремы самостоятельно.
§1.4. Линейная зависимость и линейная независимость системы векторов.
1.4.1. Определение. Линейной комбинацией векторов ![]() с коэффициентами
с коэффициентами ![]() называется вектор
называется вектор ![]() . Здесь
. Здесь ![]() − заданные числа.
− заданные числа.![]()
1.4.2. Определение. Если все коэффициенты линейной комбинации равны нулю ![]() , то она называется тривиальной. Если же среди коэффициентов линейной комбинации найдется хотя бы один отличный от нуля, то она называется нетривиальной.
, то она называется тривиальной. Если же среди коэффициентов линейной комбинации найдется хотя бы один отличный от нуля, то она называется нетривиальной.
1.4.3. Определение. Система векторов ![]() называется линейно зависимой, если существует их нетривиальная линейная комбинация, равная нулевому вектору, т.е.
называется линейно зависимой, если существует их нетривиальная линейная комбинация, равная нулевому вектору, т.е. ![]()
1.4.4. Определение. Система векторов ![]() называется линейно независимой, если только их тривиальная линейная комбинация равна нулевому вектору, т.е.
называется линейно независимой, если только их тривиальная линейная комбинация равна нулевому вектору, т.е.
![]()
1.4.5. Теорема. (Критерий линейной зависимости системы векторов линейного пространства)
Для того, чтобы система векторов линейного пространства была линейно зависима, необходимо и достаточно, чтобы один из векторов являлся линейной комбинацией остальных векторов системы.
Доказательство:
Необходимость.
Пусть система векторов ![]() линейно зависима. Покажем, что один из векторов является линейной комбинацией остальных. Из определения линейной зависимости следует, что
линейно зависима. Покажем, что один из векторов является линейной комбинацией остальных. Из определения линейной зависимости следует, что
![]()
Предположим без ограничения общности, что ![]() (в противном случае векторы могут быть перенумерованы). Разделим последнее равенство на
(в противном случае векторы могут быть перенумерованы). Разделим последнее равенство на ![]() , получим:
, получим:
![]()
то есть вектор ![]() является линейной комбинацией остальных векторов.
является линейной комбинацией остальных векторов.
Достаточность.
Пусть один из векторов является линейной комбинацией остальных, например,
![]()
Таким образом, получена нетривиальная (коэффициент при ![]() отличен от нуля) линейная комбинация векторов
отличен от нуля) линейная комбинация векторов ![]() , равная нулю-вектору, следовательно, эти векторы линейно зависимы.
, равная нулю-вектору, следовательно, эти векторы линейно зависимы.
1.4.6. Свойства линейно зависимых и линейно независимых систем векторов.
1.4.6.1. Теорема. (Свойство 1)
Всякая система векторов, включающая нулевой вектор, является линейно зависимой.
Доказательство:
Рассмотрим систему векторов ![]() . Очевидно, существует их нетривиальная линейная комбинация, равная нулю-вектору:
. Очевидно, существует их нетривиальная линейная комбинация, равная нулю-вектору:
![]()
1.4.6.2. Теорема. (Свойство 2)
Система векторов, содержащая линейно зависимую подсистему, является линейно зависимой.
Доказательство:
Пусть подсистема ![]() системы векторов
системы векторов ![]() линейно зависима, тогда
линейно зависима, тогда
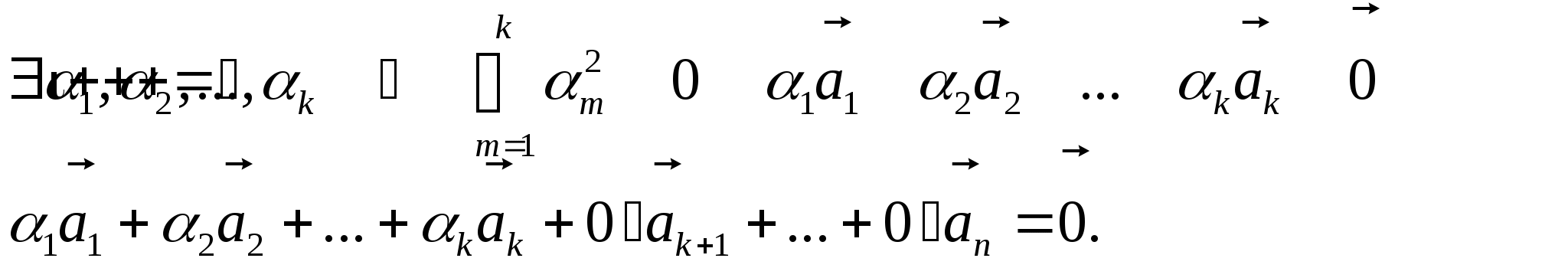
Таким образом, существует нетривиальная линейная комбинация векторов ![]() , равная нулю-вектору, то есть система векторов
, равная нулю-вектору, то есть система векторов ![]() линейно зависима.
линейно зависима.
1.4.6.3. Теорема. (Свойство 3)
Всякая подсистема линейно независимой системы векторов является линейной независимой.
Доказательство:
Используем доказательство от противного. Предположим, что у линейно независимой системы векторов ![]() найдется линейно зависимая подсистема
найдется линейно зависимая подсистема ![]() . Тогда из предыдущего свойства 2 вытекает, что система векторов
. Тогда из предыдущего свойства 2 вытекает, что система векторов ![]() линейно зависима, что противоречит условию теоремы. Нами получено противоречие, что и доказывает теорему.
линейно зависима, что противоречит условию теоремы. Нами получено противоречие, что и доказывает теорему.
1.4.7. Теорема. (О линейной зависимости двух векторов).
Два геометрических вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Доказательство очевидным образом вытекает из критерия коллинеарности векторов 1.2.8.
1.4.8. Теорема. (О линейной зависимости трех векторов).
Три геометрических вектора линейно зависимы тогда и только тогда, когда они компланарны.
Доказательство этой теоремы оставляется читателю.
Следствие.
Если векторы ![]() и
и ![]() неколлинеарны, и вектор
неколлинеарны, и вектор ![]() компланарен с векторами
компланарен с векторами ![]() и
и ![]() , то
, то ![]() линейно выражается через векторы
линейно выражается через векторы ![]() и
и ![]() (
(![]() является линейной комбинацией
является линейной комбинацией ![]() и
и ![]() ), т.е. существуют коэффициенты
), т.е. существуют коэффициенты ![]() и
и ![]() такие, что
такие, что ![]() .
.
1.4.9. Теорема. (О линейной зависимости четырех векторов).
Четыре геометрических вектора линейно зависимы.
Докажите эту теорему самостоятельно.
Следствие.
Если векторы ![]() ,
,![]() и
и ![]() некомпланарны, то любой вектор
некомпланарны, то любой вектор ![]() линейно выражается через векторы
линейно выражается через векторы ![]() ,
,![]() и
и ![]() (
(![]() является линейной комбинацией
является линейной комбинацией ![]() ,
,![]() и
и ![]() ), т.е. существуют коэффициенты
), т.е. существуют коэффициенты ![]() такие, что
такие, что ![]() .
.
§1.5. Векторное пространство. Базис.
1.5.1. Определение. Векторным пространством называется любое множество векторов, для элементов которого
а) определена операция сложения (т.е. для каждой пары векторов ![]() и
и ![]() определен третий вектор
определен третий вектор ![]() , являющийся их суммой:
, являющийся их суммой: ![]() =
= ![]() +
+![]() );
);
b) определена операция умножения вектора на действительное число (т.е. для каждого вектора ![]() и действительного числа
и действительного числа ![]() определен вектор
определен вектор ![]() ;
;
c) эти операции обладают установленными в параграфе 1.2. Линейные операции над векторами свойствами:
1. Для любых векторов ![]() и
и ![]()
![]() (коммутативность);
(коммутативность);
2. Для любых векторов ![]() ,
,![]() и
и ![]()
![]() (ассоциативность);
(ассоциативность);
3. Для любого вектора ![]()
![]() ;
;
4. Для любого вектора ![]() существует противоположный вектор
существует противоположный вектор ![]() такой, что
такой, что
![]() .
.
5. Для любого вектора ![]()
![]() (ассоциативность);
(ассоциативность);
6. Для любого вектора ![]()
![]() (дистрибутивность относительно суммы скаляров);
(дистрибутивность относительно суммы скаляров);
7. Для любых векторов ![]() и
и ![]()
![]() (дистрибутивность относительно суммы векторов);
(дистрибутивность относительно суммы векторов);
8. Для любого вектора ![]() ;
;
Примеры векторных пространств
V1 – множество векторов, расположенных на прямой;
V2 – множество векторов, расположенных на плоскости;
V3 – множество векторов, расположенных в пространстве.
1.5.2. Определение. Базисом векторного пространства назы7ается линейно независимая упорядоченная совокупность векторов такая, что любой вектор пространства является линейной комбинацией векторов этой системы.
1.5.3. Определение. Размерностью векторного пространства называется количество векторов в любом его базисе.
Замечание.
Базисом пространства V1 векторов, расположенных на прямой, является любой ненулевой вектор этого пространства. Размерность пространства V1 равна 1.
Базисом пространства V2 векторов, расположенных на плоскости, является любая пара некомпланарных векторов этого пространства. Размерность пространства V2 равна 2.
Базисом пространства V3 векторов, расположенных в пространстве, является любая тройка некомпланарных векторов. Размерность пространства V3 равна 3.
1.5.4. Определение. Пусть ![]() - базис пространства V3. Представление геометрического вектора
- базис пространства V3. Представление геометрического вектора ![]() в виде линейной комбинации векторов базиса
в виде линейной комбинации векторов базиса ![]()
![]()
называется разложением вектора ![]() по базису
по базису ![]() . Коэффициенты линейной комбинации
. Коэффициенты линейной комбинации ![]() называются координатами вектора
называются координатами вектора ![]() в базисе
в базисе ![]() .
.
1.5.5. Теорема. (О разложении вектора по базису).
Всякий вектор может быть разложен по некоторому базису векторного пространства единственным образом.
Доказательство:
От противного. Рассмотрим разложение некоторого вектора ![]() по произвольному базису
по произвольному базису ![]() не единственно:
не единственно:
![]() ;
;
![]() .
.
Вычитая равенства, получим ![]() .
.
Из определения 1.5.2 вытекает линейная независимость векторов ![]() .
.
Следовательно, лишь тривиальная их линейная комбинация равна нулевому вектору, откуда ![]() , что и требовалось доказать.
, что и требовалось доказать.
Замечание.
Из доказанной теоремы следует, что координаты данного вектора в заданном базисе определяются однозначно.
1.5.6. Теорема. (Линейные операции с векторами в координатной форме).
При сложении векторов их соответствующие координаты складываются, а при умножении вектора на число все его координаты умножаются на это же число.
Доказательство:
1. Докажем первую часть теоремы, касающуюся сложения векторов.
Пусть разложения векторов ![]() и
и ![]() в базисе
в базисе ![]() имеют вид:
имеют вид:
![]() ;
; ![]() .
.
Тогда
![]() .
.
2. Аналогично получим
![]() .
.
Следствие. Критерий коллинеарности векторов.
Для того, чтобы два геометрических вектора были коллинеарными, необходимо и достаточно, чтобы их соответствующие координаты в некотором базисе были пропорциональными.
Доказательство следует из теорем 1.5.6 и 1.2.8. Действительно, коллинеарность векторов ![]() и
и ![]() согласно теореме 1.2.8 эквивалентна условию
согласно теореме 1.2.8 эквивалентна условию ![]() , что означает пропорциональность соответствующих координат в произвольном базисе.
, что означает пропорциональность соответствующих координат в произвольном базисе.
1.5.7. Определение. Базис векторного пространства, состоящий из попарно перпендикулярных векторов единичной длины, называется ортонормированным.
Замечание.
Ортонормированный базис в пространстве V2 обычно обозначается ![]() , в пространстве V3
, в пространстве V3 ![]() .
.
§1.6. Скалярное произведение двух векторов.
1.6.1. Определение. Скалярным произведением векторов ![]() и
и ![]() называется действительное число, равное произведению длин векторов на косинус угла между ними.
называется действительное число, равное произведению длин векторов на косинус угла между ними.
Скалярное произведение векторов ![]() и
и ![]() обозначается
обозначается ![]() или
или ![]() . Итак,
. Итак,
![]() .
.
1.6.2. Теорема. (Свойства скалярного произведения двух векторов).
1. ![]() ;
;
2. ![]() (скалярный квадрат вектора равен квадрату его длины);
(скалярный квадрат вектора равен квадрату его длины);
3. ![]() ;
;
4. ![]() ;
;
5. ![]() ;
;
6. ![]() ;
;
7. если ![]() , то
, то ![]() ;
;
8. если ![]() , то либо хотя бы один из векторов
, то либо хотя бы один из векторов ![]() и
и ![]() равен нулю, либо
равен нулю, либо ![]() и
и ![]() ортогональны.
ортогональны.
Доказательство.
Первое и второе свойства непосредственно следуют из определения:
1. косинус – четная функция, поэтому неважно, как отсчитывается угол – от ![]() к
к ![]() или от
или от ![]() к
к ![]() ;
;
2. ![]() .
.
3. Используем первое свойство ортогональной проекции (Теорема 1.3.3.1) ![]()
4. Используем предыдущее свойство 3 и второе свойство ортогональной проекции (Теорема 1.3.3.2):
![]() .
.
5. Используем свойство 3 и третье свойство ортогональной проекции (Теорема 1.3.3.3):
![]() .
.
Шестое, седьмое и восьмое свойства очевидны (если ![]() , то
, то ![]() ; если
; если ![]() , то
, то ![]() ; если произведение равно нулю, то необходимо один из сомножителей, входящих в определение (
; если произведение равно нулю, то необходимо один из сомножителей, входящих в определение (![]() , либо
, либо ![]() , либо
, либо ![]() ) равен нулю).
) равен нулю).
Замечание 1.
Так как направление нуль-вектора произвольно, то восьмое свойство можно переформулировать как необходимое и достаточное условие ортогональности векторов:
два вектора ортогональны тогда и только тогда, когда их скалярное произведение равно нулю.
Замечание 2.
Механический смысл скалярного произведения заключается в следующем: если материальная точка под воздействием силы ![]() перемещается на вектор
перемещается на вектор ![]() , то совершаемая этой силой работа равна скалярному произведению
, то совершаемая этой силой работа равна скалярному произведению ![]() на
на ![]() :
:
![]() .
.
1.6.3. Теорема. (Выражение скалярного произведения двух векторов, заданных в ортонормированном базисе).
В ортонормированном базисе скалярное произведение двух векторов равно сумме попарных произведений их соответствующих координат.
Доказательство:
Пусть в ортонормированном базисе ![]() заданы векторы
заданы векторы
![]() ,
, ![]() .
.
Заметим, что вследствие ортонормированности базиса
![]()
Тогда
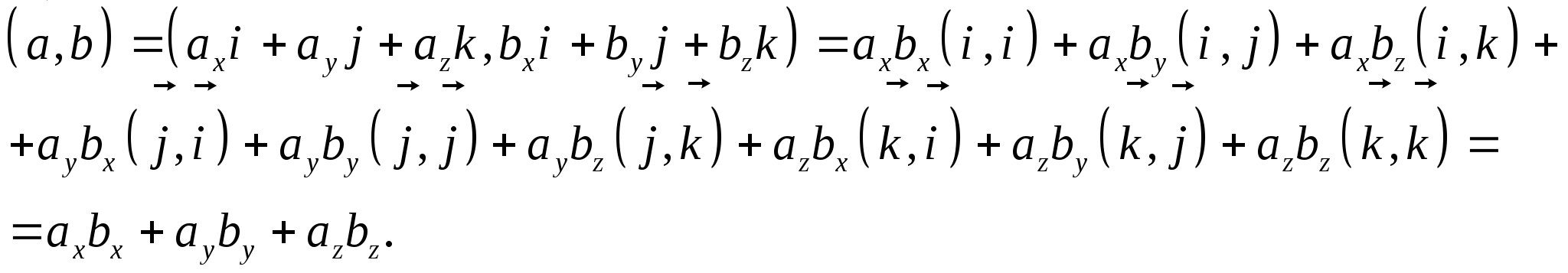
Следствие 1. (Вычисление длины вектора в ортонормированном базисе).
![]()
Следствие 2. (Вычисление координат орта вектора в ортонормированном базисе)
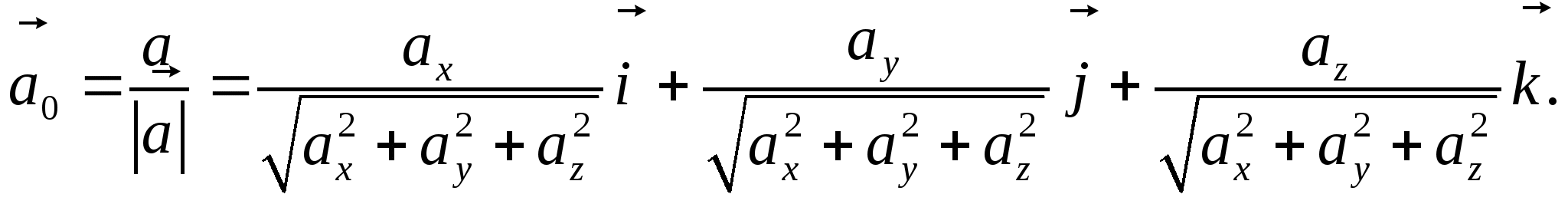
1.6.4. Вычисление ортогональной проекции вектора на направление в ортонормированном базисе
Из свойства 3 скалярного произведения (Теорема 1.6.2)
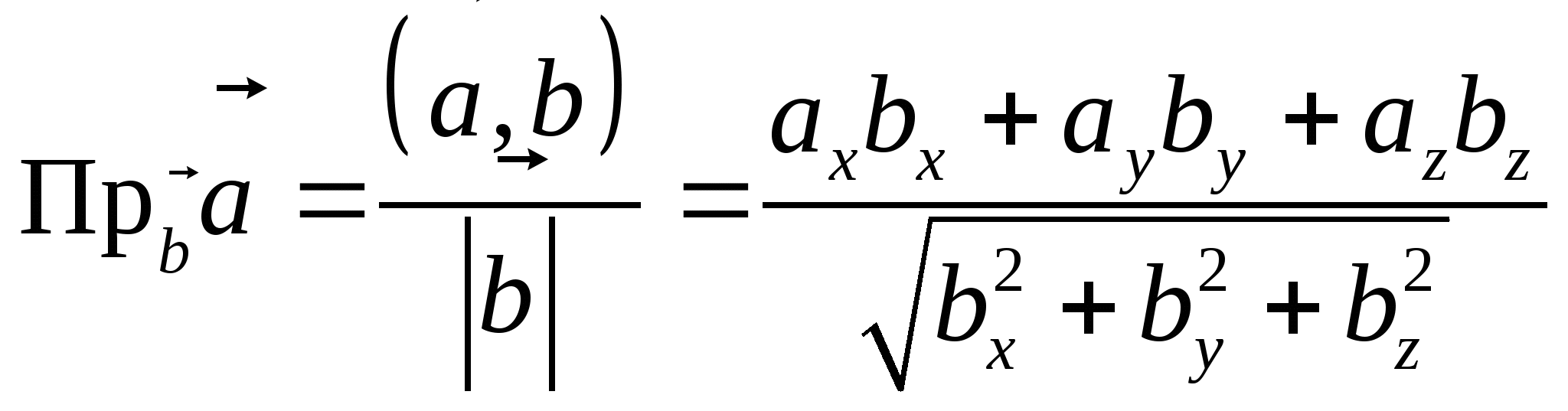 .
.
Замечание.
Если ![]() , то
, то 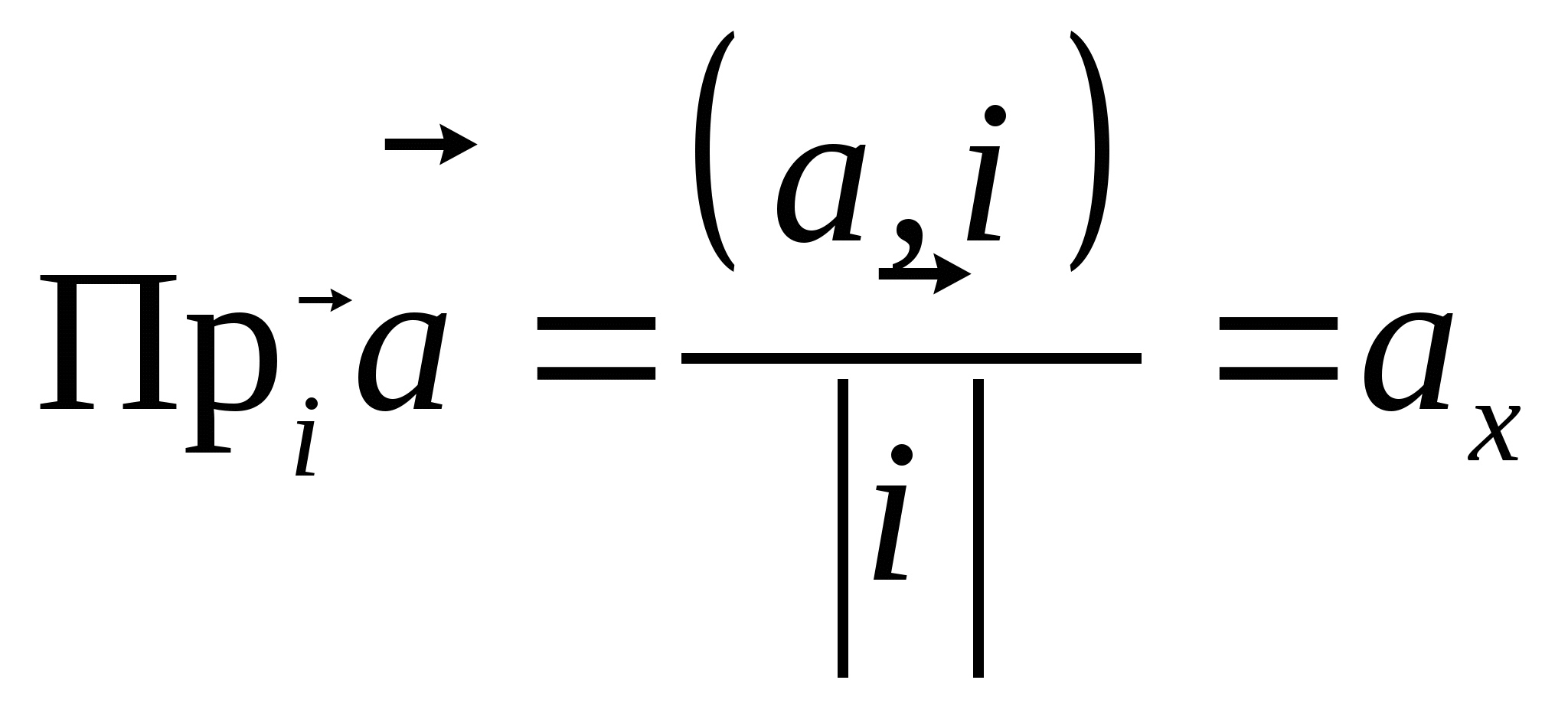 . Аналогично,
. Аналогично, ![]() . Таким образом, координаты вектора в ортонормированном базисе являются его ортогональными проекциями на направления, заданные соответствующими ортами.
. Таким образом, координаты вектора в ортонормированном базисе являются его ортогональными проекциями на направления, заданные соответствующими ортами.
1.6.5. Вычисление угла между векторами в ортонормированном базисе.
Из определения скалярного произведения получим
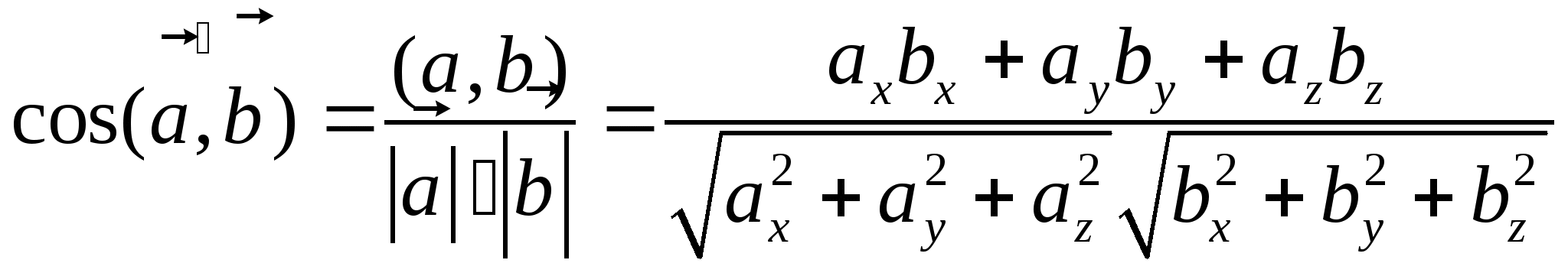 ,
,
откуда:
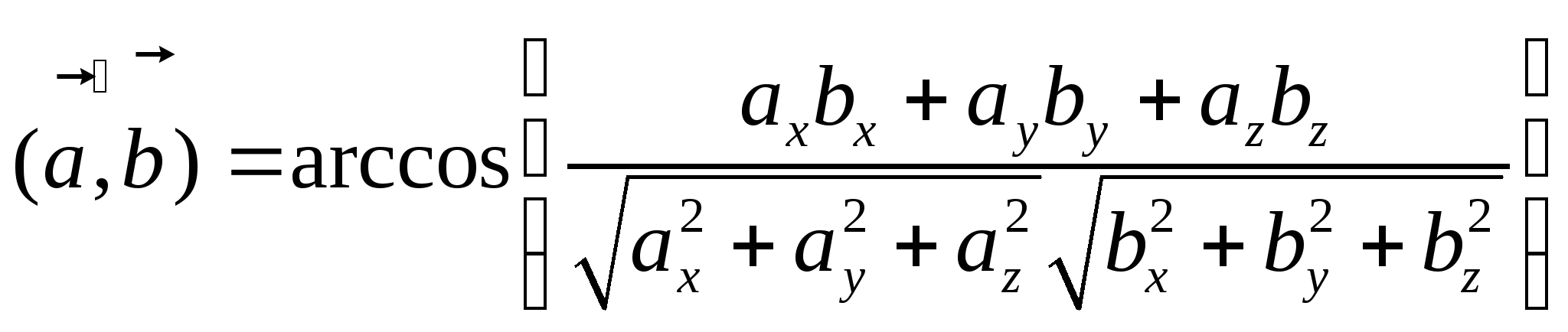 .
.
1.6.6. Определение. Косинусы углов, которые отличный от нуля вектор образует с векторами ортонормированного базиса, называются направляющими косинусами.
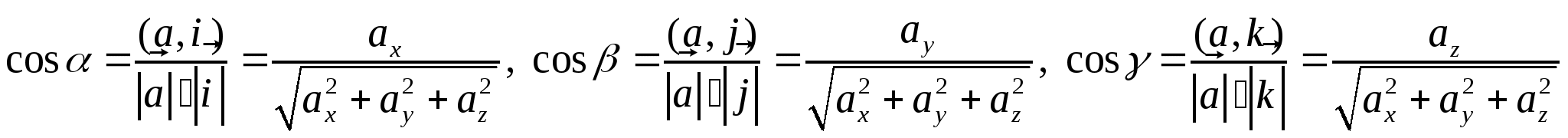 .
.
Замечание 1.
Легко видеть, что направляющие косинусы удовлетворяют соотношению
![]() .
.
Замечание 2.
Из полученных выражений для направляющих косинусов видно, что они совпадают с координатами орта вектора.
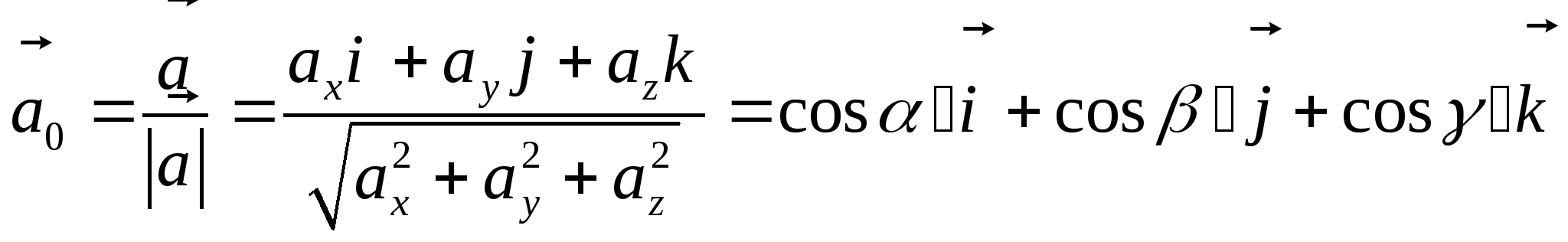 .
.
Лекция 3.
§1.7. Векторное произведение двух векторов.
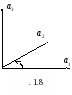
1.7.1. Определение. Упорядоченная тройка некомпланарных векторов называется правой, если при приведении этих векторов к общему началу ближайший поворот от первого вектора ко второму виден с конца третьего вектора совершающимся против часовой стрелки. В противном случае тройка называется левой.
Например, на Рис. 1.8. показана правая тройка векторов ![]() .
.
Замечание 1.
Цикличная перестановка векторов не меняет ориентации тройки; (то есть после цикличной перестановки она остается либо правой, либо левой).
Замечание 2.
Тройки компланарных векторов не относят ни к правым, ни к левым.
Замечание 3.
Стандартный ортонормированный базис ![]() пространства V3 задается правой тройкой ортов.
пространства V3 задается правой тройкой ортов.
1.7.2. Определение. Векторным произведением векторов ![]() и
и ![]() называется вектор
называется вектор ![]() , длина и направление которого определяются следующими условиями:
, длина и направление которого определяются следующими условиями:
1. ![]() ;
;
2 ![]() ;
;
3. ![]() ,
, ![]() ,
, ![]() - правая тройка (если векторы
- правая тройка (если векторы ![]() и
и ![]() не коллинеарны).
не коллинеарны).
Векторное произведение векторов ![]() и
и ![]() обозначается
обозначается ![]() или
или ![]() .
.
1.7.3. Теорема. (Геометрический смысл векторного произведения двух векторов).
Длина векторного произведения векторов ![]() и
и ![]() равна площади параллелограмма, построенного на этих векторах.
равна площади параллелограмма, построенного на этих векторах.
Доказательство очевидно.
1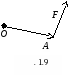 .7.4. Механический смысл векторного произведения двух векторов.
.7.4. Механический смысл векторного произведения двух векторов.
Если к точке А приложена сила ![]() , то момент этой силы относительно точки О равен
, то момент этой силы относительно точки О равен ![]() (Рис. 1.9).
(Рис. 1.9).
1.7.5. Теорема. (Свойства векторного произведения двух векторов).
1 .
. ![]() ; (антикоммутативность)
; (антикоммутативность)
2. ![]() ;
;
3. ![]() ;
;
4. ![]() ;
;
5. ![]() ;
;
6.![]() .
.
Доказательство:
Свойства 2, 3, 4 и 5 вытекают непосредственно из определения векторного произведения 1.7.2. Свойство 1 также очевидно, поскольку при перемене порядка сомножителей векторы ![]() ,
, ![]() и
и ![]() , очевидно, образуют левую тройку (см. Рис. 1.10). Свойство 6 будет доказано позднее, после свойств смешанного произведения трех векторов.
, очевидно, образуют левую тройку (см. Рис. 1.10). Свойство 6 будет доказано позднее, после свойств смешанного произведения трех векторов.
1.7.6. Теорема. (О векторном произведении векторов ортонормированного базиса).
![]() .
.
Доказательство:
Докажем первое равенство ![]() . Рассмотрим вектор
. Рассмотрим вектор ![]() . Из определения векторного произведения 1.7.2
. Из определения векторного произведения 1.7.2 ![]() Так как векторы
Так как векторы ![]() образуют правую тройку, то
образуют правую тройку, то ![]() .
.
Доказательство остальных равенств полностью аналогично.
1.7.7. Теорема. (Выражение векторного произведения двух векторов, заданных в ортонормированном базисе).
Координаты векторного произведения векторов ![]() и
и ![]() равны алгебраическим дополнениям элементов первой строки символического определителя
равны алгебраическим дополнениям элементов первой строки символического определителя
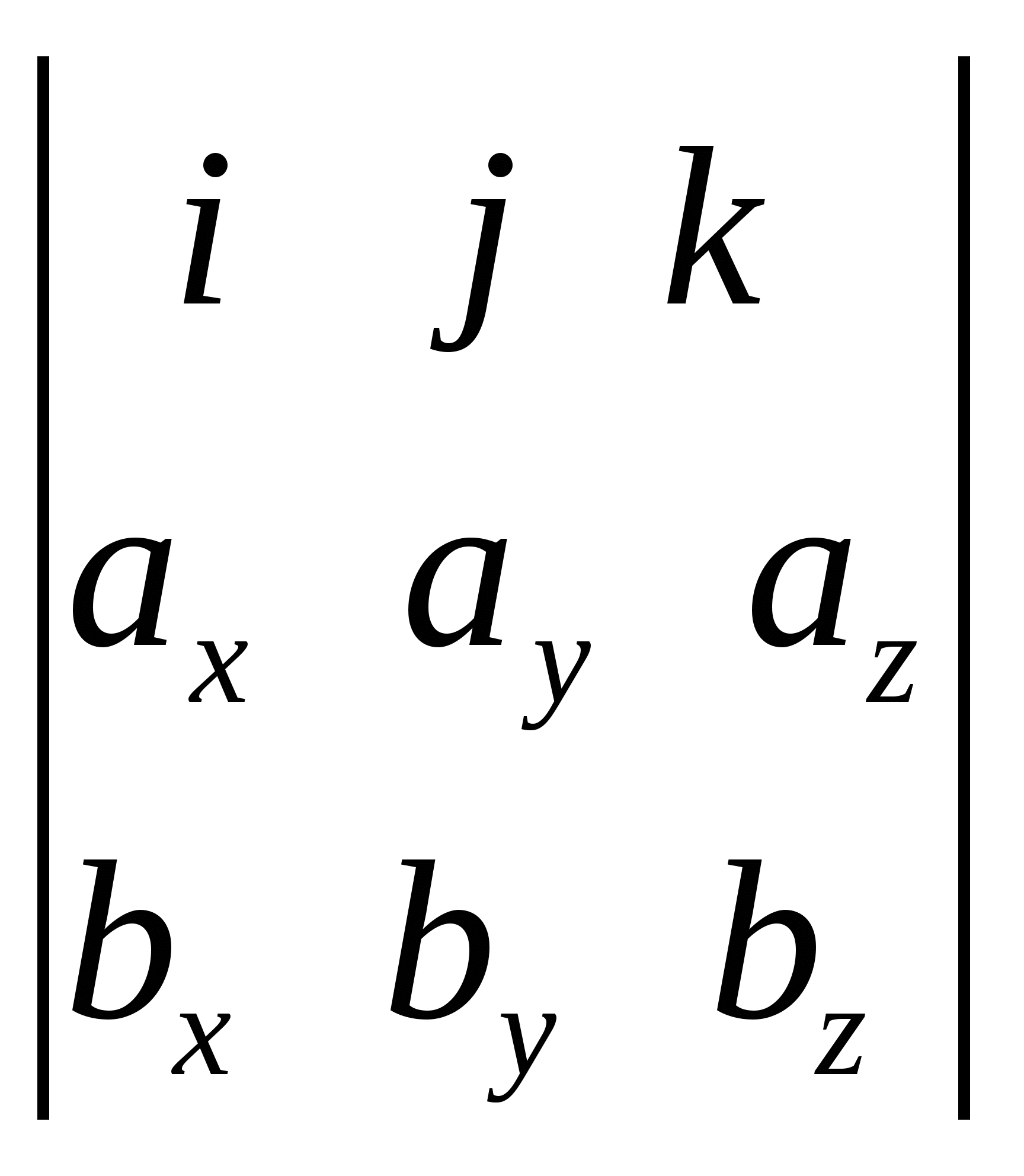 .
.
Доказательство:
Пусть векторы ![]() и
и ![]() имеют в ортонормированном базисе разложения
имеют в ортонормированном базисе разложения
![]() ,
, ![]() .
.
Тогда по свойству 6 векторного произведения

Используя предыдущую теорему 1.7.7, и очевидные равенства ![]() получим
получим
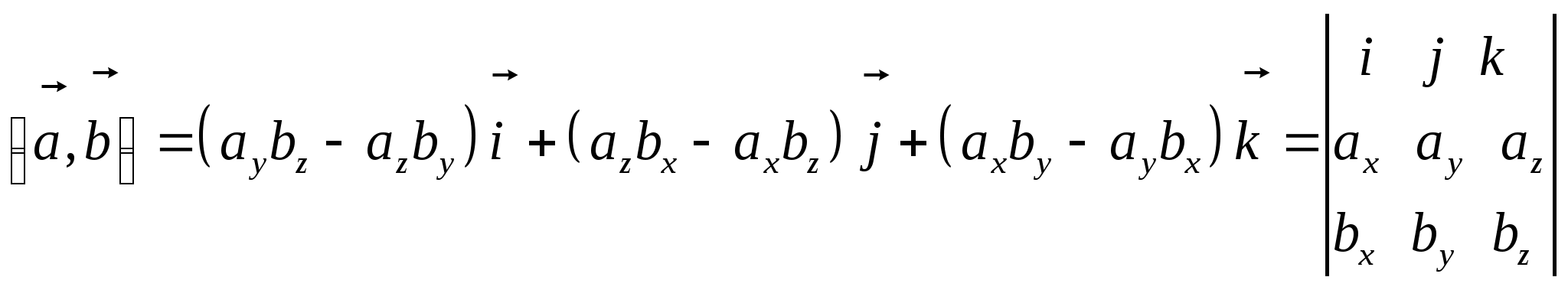 .
.
1.7.8. Двойное векторное произведение.
Вектор ![]() называется двойным векторным произведением векторов
называется двойным векторным произведением векторов ![]() . Отметим равенство
. Отметим равенство ![]() .
.
Доказательство предоставляется читателю.
§1.8. Смешанное произведение трех векторов.
1.8.1. Определение. Смешанным произведением трех векторов называется число, равное скалярному произведению векторного произведения первых двух векторов на третий вектор. Смешанное произведение векторов ![]() обозначается
обозначается ![]() или
или ![]() .
.
![]()
1.8.2. Теорема. (Геометрический смысл смешанного произведения трех векторов).
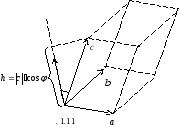
Модуль смешанного произведения векторов ![]() равно объему параллелепипеда, построенного на этих векторах. Смешанное произведение положительно, если тройка векторов
равно объему параллелепипеда, построенного на этих векторах. Смешанное произведение положительно, если тройка векторов ![]() – правая, и отрицательно, если эта тройка – левая (если векторы
– правая, и отрицательно, если эта тройка – левая (если векторы ![]() компланарны, то их смешанное произведение равно нулю).
компланарны, то их смешанное произведение равно нулю).
![]() .
.
Доказательство:
V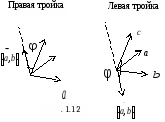 пар =
пар = ![]() . Справа в этом равенстве стоит модуль смешанного произведения. Знак смешанного произведения определяется знаком косинуса: если тройка
. Справа в этом равенстве стоит модуль смешанного произведения. Знак смешанного произведения определяется знаком косинуса: если тройка ![]() – правая, то векторы
– правая, то векторы ![]() и
и ![]() расположены в одном полупространстве относительно плоскости векторов
расположены в одном полупространстве относительно плоскости векторов ![]() и
и ![]() ,
, ![]() ,
, ![]() ; если тройка
; если тройка ![]() – левая, то векторы
– левая, то векторы ![]() и
и ![]() расположены в разных полупространствах относительно плоскости векторов
расположены в разных полупространствах относительно плоскости векторов ![]() и
и ![]() ,
, ![]() ,
, ![]() ; если компланарны, то высота параллелепипеда равна нулю, и Vпар =0.
; если компланарны, то высота параллелепипеда равна нулю, и Vпар =0.
Следствие.
Объем тетраэдра, построенного на трех векторах, равен одной шестой модуля их смешанного произведения
![]() .
.
1.8.3. Теорема. (Свойства смешанного произведения).
1. Если один из трех сомножителей равен нулю-вектору, то их смешанное произведение равно нулю ![]() ;
;
2. Критерий компланарности трех векторов: для того, чтобы три вектора были компланарными, необходимо и достаточно, чтобы их смешанное произведение было равно нулю;
3. ![]() ;
;
4. ![]() ;
;
5. ![]() ;
;
Доказательство:
Свойства 1 и 4 следуют из определения смешанного произведения трех векторов 1.8.1. Свойство 3 следует из доказанной теоремы 1.8.2. Действительно, при перестановке сомножителей в смешанном произведении, величина объема параллелепипеда сохраняется, а знак смешанного произведения определяется ориентацией тройки. Докажем свойство 5:
![]() Теперь докажем свойство 2.
Теперь докажем свойство 2.
Необходимость.
Пусть векторы ![]() компланарны. Тогда, параллелепипед, построенный на этих векторах, вырождается в плоскую фигуру, следовательно, его объем равен нулю, то есть
компланарны. Тогда, параллелепипед, построенный на этих векторах, вырождается в плоскую фигуру, следовательно, его объем равен нулю, то есть ![]() .
.
Достаточность.
Пусть ![]() . Тогда из определения смешанного произведения 1.8.1
. Тогда из определения смешанного произведения 1.8.1 ![]() . Если
. Если ![]() , то либо один из векторов
, то либо один из векторов ![]() и
и ![]() является нулевым, тогда векторы
является нулевым, тогда векторы ![]() компланарны, либо
компланарны, либо ![]() и
и ![]() являются коллинеарными векторами, тогда векторы
являются коллинеарными векторами, тогда векторы ![]() компланарны. Если
компланарны. Если ![]() , то вектор
, то вектор ![]() является нулевым, то есть векторы
является нулевым, то есть векторы ![]() компланарны. Если, наконец,
компланарны. Если, наконец, ![]() , то это означает, что векторы
, то это означает, что векторы ![]() и
и ![]() ортогональны. Заметим, что из определения векторного произведения вектор
ортогональны. Заметим, что из определения векторного произведения вектор ![]() ортогонален также векторам
ортогонален также векторам ![]() и
и ![]() , а это означает, что векторы
, а это означает, что векторы ![]() параллельны некоторой плоскости, то есть компланарны.
параллельны некоторой плоскости, то есть компланарны.
Замечание.
Докажем теперь свойство 6 векторного произведения:
![]() .
.
Покажем, что векторы в левой и правой частях этого равенства имеют одинаковые координаты. Координаты вектора равны скалярным произведениям этого вектора на базисные орты (см. Замечание к п. 1.6.4.). Рассмотрим данное векторное равенство в координатах. Используем свойство 5 смешанного произведения:
![]()
Аналогично можно показать равенство остальных координат. Таким образом, координаты векторов в левой и правой частях равенства равны, следовательно, по теореме 1.5.5. о разложении вектора по базису, эти векторы равны.
1.8.4. Теорема. (Выражение смешанного произведения двух векторов, заданных в ортонормированном базисе).
Смешанное произведение трех векторов в ортонормированном базисе равно определителю, строками которого являются координаты этих векторов данном базисе.
Доказательство:
Пусть векторы ![]() ,
,![]() и
и ![]() имеют в ортонормированном базисе разложения
имеют в ортонормированном базисе разложения
![]() ,
, ![]() ,
, ![]() .
.
Тогда
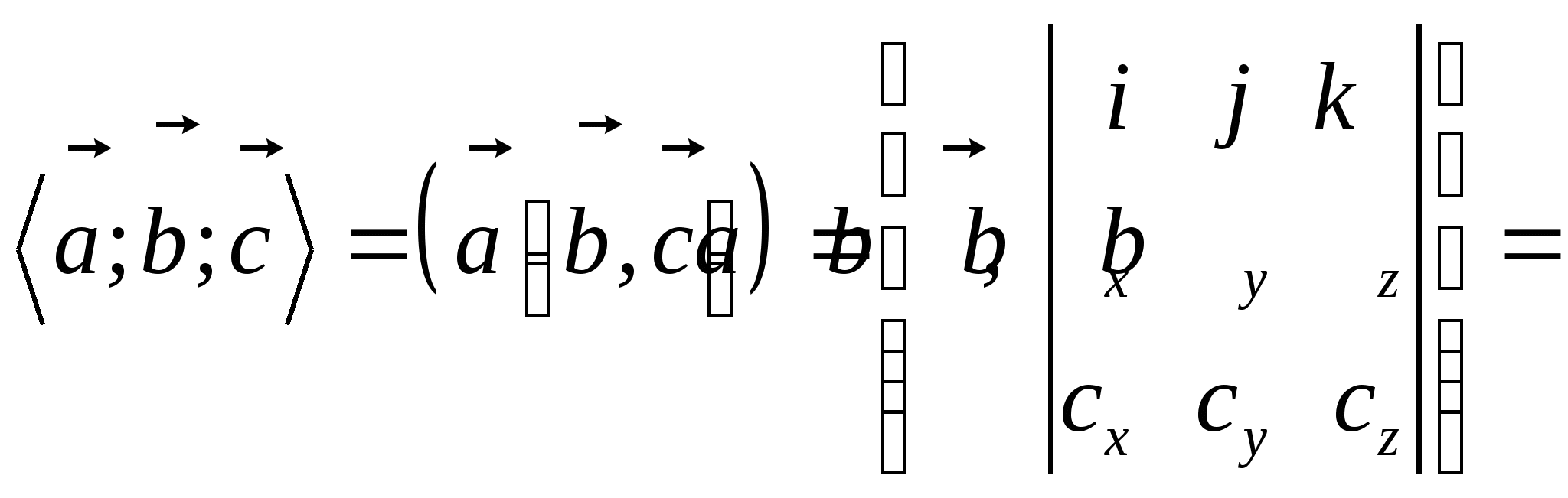
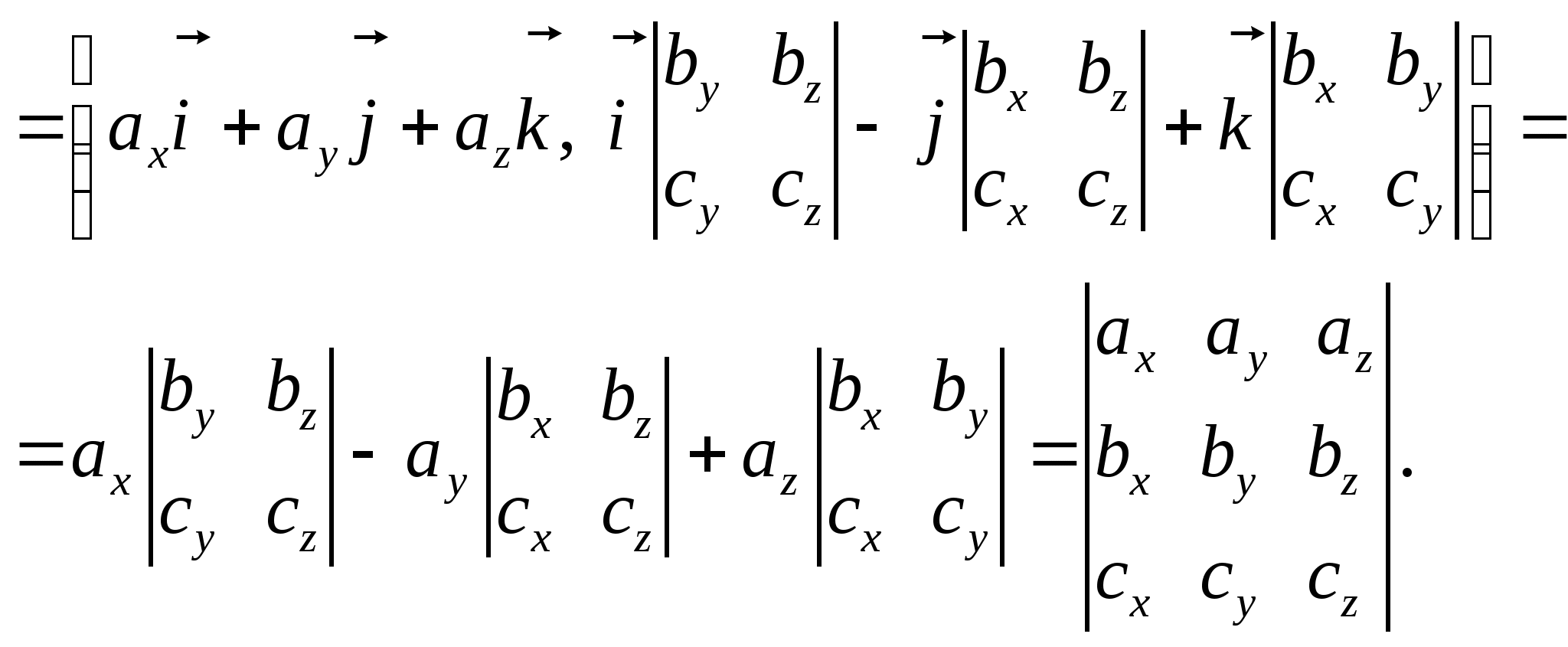
В завершение главы отметим утверждение, являющееся прямым следствием доказанной теоремы и критерия компланарности (свойство 2 смешанного произведения):
Три вектора компланарны тогда и только тогда, когда определитель, строками которого являются координаты этих векторов в ортонормированном базисе, равен нулю.

| Автор | |
|---|---|
| Дата добавления | 13.05.2019 |
| Раздел | Алгебра |
| Подраздел | Конспект урока |
| Просмотров | 2235 |
| Номер материала | 6218 |