
Открытый урок по теме "Применение распределительного свойства умножения" 6 класс
Открытый урок по математике в 6а классе по теме: "Применение распределительного свойства умножения"
Цель:
Образовательная: систематизировать и обобщить известные учащимся сведения о распределительном свойстве умножения; выработать умения выполнять умножение дробных чисел, используя распределительное свойство умножения.
Развивающая: поддержать у учащихся интерес к изучаемому материалу на протяжении всего урока, активизируя работу учащихся за счёт использования на уроке различных форм работы. Развивать самостоятельность, внимание, математическое мышление.
Воспитательная: воспитание таких качеств личности как аккуратность в работе, трудолюбие, умение преодолевать трудности в процессе решения задач.
Методы обучения: фронтальная работа, самостоятельная работа, работа по вариантам.
Оборудование: компьютер, проектор, экран, презентация.
1. Организационный момент
-Давайте, ребята, улыбнемся сегодняшнему дню, создадим себе хорошее настроение, и проведем с вами необычный урок ,на котором присутствуют гости
2. Актуализация знаний.
Сообщение темы урока
Учитель: С этим свойством мы уже знакомы:
Умножим
26 • 4 = 104
Как мы это делаем:
(20 + 6) • 4 = 20 • 4 + 6 • 4 = 104
49 • 3 = 147
(50 – 1) • 3 = 150 – 3 = 147
Что же даёт нам применение распределительного свойства:
УПРОЩАТЬ ВЫЧИСЛЕНИЯ.
Давайте запишем формулировку данного свойства:
относительно суммы: (a+b)c=ac+bc
относительно вычитания: (a-b)c=ac-bc, где a>b
Наша с вами цель сегодня:
Научится применять данные свойства относительно действий с обыкновенными дробями, смешанными числами, научится упрощать выражения и составлять выражения для решения задач.
Пример 1: Найдем значения выражения
![]()
Решение: Представим вначале число ![]() в виде суммы его целой части и дробной части:
в виде суммы его целой части и дробной части: ![]() , а затем применим распределительное свойство. Получим:
, а затем применим распределительное свойство. Получим:
![]()
Вывод: Чтобы умножить смешанное число на натуральное число можно
1) умножить целую часть на натуральное число;
2) умножить дробную часть на это натуральное число;
3) сложить полученные результаты.
Пример 2. Выполните умножение:
а)![]() ; б)
; б)![]() ;
;
в)![]() ; г)
; г)![]() ;
;
Образец:
![]()
![]()
Пример3: Найдем значение выражения
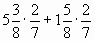
Решение. На основе распределительного свойства умножения представим эту сумму в виде произведения суммы ![]() и числа
и числа ![]() :
:
![]()
Вывод: общий множитель (одинаковое число в каждом произведении) можно выносить за скобки. Выполни упражнения в тетради, правильно оформляя:
Пример4: Выполните упражнение в тетради (упростите выражения):
а) ![]() ; б)
; б)![]() ; в)
; в)![]() ;
;
г) ![]() ; д)
; д)![]() ; е)
; е)![]()
ж)![]() з)
з)![]()
Решим уравнение 5:
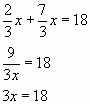
![]()
Ответ: х = 6
Решите задачу 6:
Продолжительность жизни березы 150 лет. Сосна живет в 2![]() раза больше березы, а мамонтово дерево живет в 5 раз дольше сосны. Какова продолжительности жизни Мамонтова дерева?
раза больше березы, а мамонтово дерево живет в 5 раз дольше сосны. Какова продолжительности жизни Мамонтова дерева?
Решите задачу 7:
Квартира состоит из двух комнат. Длина большей комнаты 5![]() м, а ширина 4 м. Длина меньшей комнаты 4 м, а ширина 3
м, а ширина 4 м. Длина меньшей комнаты 4 м, а ширина 3![]() м. На сколько площадь одной комнаты меньше площади другой?
м. На сколько площадь одной комнаты меньше площади другой?
Пример8: Найдите значение выражения:
![]() , если
, если 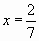
Пример 9:
Составьте выражение для решения задачи:
Сумма трех чисел равна n. Первое число составляет ![]() этой суммы, а второе
этой суммы, а второе ![]() этой суммы. Чему равно третье число?
этой суммы. Чему равно третье число?
Закрепление
Тест
При сложении дробей с одинаковыми знаменателями знаменатель остается тем же, а числители складываются.(+)
Чтобы вычесть дроби с разными знаменателями, надо привести их к наибольшему общему знаменателю и выполнить вычитание дробей с одинаковыми знаменателями.(-)
При сложении целого числа и смешанного получается смешанное число.(+)
Чтобы выделить целую часть из неправильной дроби, надо числитель умножить на знаменатель.(-)
Если при сложении дробей получается неправильная дробь, то надо результат записать в виде смешанного числа.(+)
Произведение двух дробей есть дробь, в числителе которой произведение знаменателей, а в знаменателе – произведение числителей.(-)
Чтобы из единицы вычесть дробь, надо единицу записать в виде неправильной дроби со знаменателем, равным знаменателю дроби, которую вычитаем.(+)
При умножении двух смешанных дробей, надо перемножить целые части и сложить с произведением дробных частей.(-)
При умножении целого числа на дробь, надо целое число умножить на числитель, а знаменатель оставить прежним.(+)
Соедините знаки «+», расположенные по одной линии. Что получили? Каким образом полученный символ связан с математикой? Где он нам встречается? Правильно, это х – неизвестное в уравнении.
Итог урока
Решение уравнений с использованием распределительного свойства умножения.
![]() , 6x + 25 = 29, 6x = 29 – 25, 6x = 4, x =
, 6x + 25 = 29, 6x = 29 – 25, 6x = 4, x = ![]() , Ответ:
, Ответ: ![]() .
.
Дополнительные уравнения на карточках:
(![]() х + 2
х + 2![]() )·28=72 (х=1)
)·28=72 (х=1)
(![]() х - 1
х - 1![]() )·44 = 12 (х=3)
)·44 = 12 (х=3)
(![]() -
- ![]() х)·14 = 6 (х=
х)·14 = 6 (х=![]() )
)
28х·1![]() - 28х·
- 28х·![]() = 1 (х=
= 1 (х=![]() )
)
Домашнее задание
№552(д,е), №559.
Отзыв коллег на открытый урок в 6 а классе на тему:
"Применение распределительного свойства умножения"
Урок проводился в соответствии с тематическим планированием. Он второй урок по теме « Применение распределительного свойства умножения». Урок построен с опорой на предыдущие уроки и ранее изученные темы: « Наибольший общий делитель». «Основное свойство дроби», « Сокращение дробей», «Умножение дробей».
Урок был спланирован как комбинированный урок формирования и комплексного применения знаний.Учитывая практическую важность знаний и умений, тренируемых на уроке, для дальнейшего изучения математики, алгебры была сформулирована общая цель – выработка умений самостоятельно применять эти знания, усваивать способы и действия в комплексе. Все этапы урока были связаны между собой, прослеживался плавный переход от одного этапа к другому. Это придало уроку целостность и завершенность.
Для активации мыслительной деятельности были использованы следующие приёмы и методы : презентация, которая решила вопрос наглядности, четкой последовательности организации, дало возможность рационально использовать время урока. Деятельность была мотивирована разными её видами – работа с учебником, парная и групповая , самостоятельная работы, устные и письменные упражнения.Учащиеся выполняли оценочную работу, анализируя способ решения , предложенный учителем, путем наблюдения и рассуждения выводили алгоритм, сравнивали несколько вариантов.В оценочной деятельности были применены – методы самопроверки, взаимопроверки, сочетались с фронтальной проверкой на экране.Отметочная оценка деятельности детей не использована, т.к. этот урок объяснения нового материала, цель мотивировать детей через оценку словесную - молодец, правильно, подумай и т.д. Дети оценивали себя сами.
Если говорить о результативности урока , то на наш взгляд он был получен в содержательной части. Было видно, что дети знают
-Правило сокращения дробей
-Правила сложения , умножения дроби на натуральное число
-Распределительное свойство умноженияумеют их применять и на основе, выведенного на уроке алгоритма умножать смешанное число на натуральное число.
Личностные результаты тоже есть. Дети получили стимул для самостоятельного обучения.Занятость учащихся была обеспечена разнообразными заданиями. Процесс усвоения знаний был управляемым. Дети вступали в диалог, эмоциональный фон урока был позитивным.
Домашнее задание было дано по аналогии с примерами, разобранными на уроке, Эльмира Пахрудиновнасопроводила их пошаговой инструкцией.
Отзыв коллег на открытый урок в 6 а классе на тему:
"Применение распределительного свойства умножения"
Для урока была характерна внешняя и внутреняя культура: организованное начало и окончание урока, рациональное использование учебного времени, целесообразность использования наглядного и дидактического материала, доброжелательная, эмоноционально-психологическая атмосфера урока.
Для фронтального опроса подобраны задачи, которые не требуют глубоких научных знаний, поэтому испытать радость успеха мог каждый ребёнок, независимо от успеваемости по предмету. Эта и дальнейшая работа позволили реализовать мне принцип личностно-ориентированного обучения: ребёнок учится только через действие.
Домашнее задание содержит задание творческого характера, что направлено на создание ситуации успеха для слабоуспевающих учеников и развитие кругозора для всех членов классного коллектива.
Работа в парах, самостоятельная работа учеников у доски с комментариями позволили Эльмире Пахрудиновне решить очередной принцип личностно-ориентированного обучения: ребёнок учится от других учеников так же как от учителя.
Содержание урока соответствует возрастным особенностям детей, объём заданий дозирован. Каждый этап урока был нацелен на достижение определённого результата. Все этапы урока логически взаимосвязаны. Задания направлены не только на отработку математических умений, но и ориентируют детей на активную жизненную позицию по охране окружающей среды.
Доброжелательная обстановка, позитивный настрой на урок, подбор заданий, рациональное использование времени позволили избежать перегрузок во время урока, помог каждому ребёнку на занятии продвинуться в своём индивидуальном развитии. Учащиеся быстро включились в деловой ритм. Они были готовы к восприятию данной темы и имели достаточный запас знаний.
Учащиеся под руководством учителя самостоятельно рассуждали, решали возникающие познавательные задачи, анализировали, обобщали, делали выводы, тем самым формировали осознанные прочные знания.
Родители 6 а класса

| Автор | |
|---|---|
| Дата добавления | 21.10.2019 |
| Раздел | Математика |
| Подраздел | Конспект урока |
| Просмотров | 1882 |
| Номер материала | 6367 |