
Презентация "Двугранный угол"

Краткое описание документа:
Презентация «Двугранный угол» является наглядным пособием для проведения урока по геометрии по данной теме. В ходе презентации представлено понятие двугранного угла, сравнивая его с линейным углом, приведены примеры встречающихся в жизни двугранных углов, рассматривается важная теорема о связи линейного и двугранного угла, а также рассматривается решение задач, для решения которых используется изученный материал.
С помощью анимации и других приемов в презентации продемонстрированы основные объекты изучения, представляющие собой понятия стереометрии. Эффективность презентации в процессе обучения обусловлена множеством приемов, которые положительно влияют на процессы мышления и запоминания, удерживают внимание учеников на обучении. С помощью этих средств достигается глубокое понимание материала, запоминание терминов и хода решения задач.
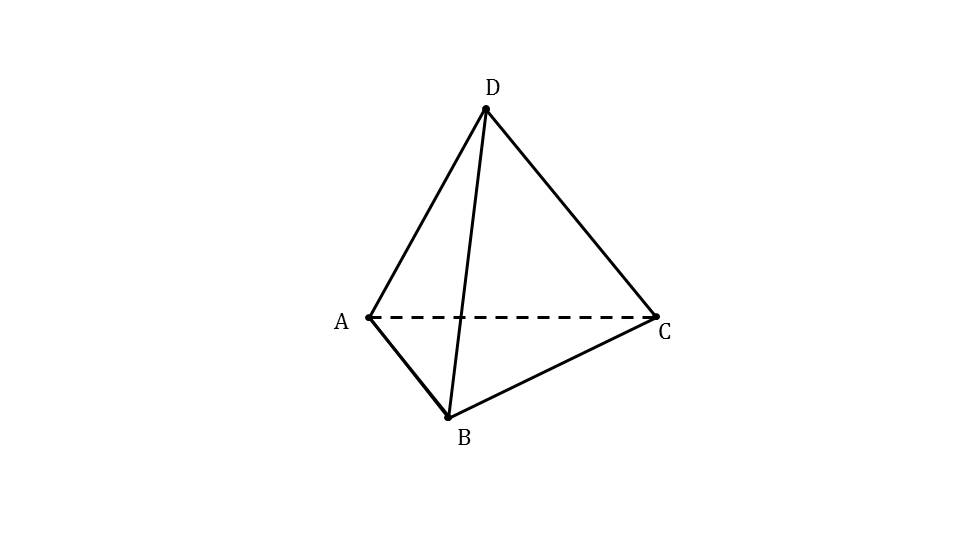
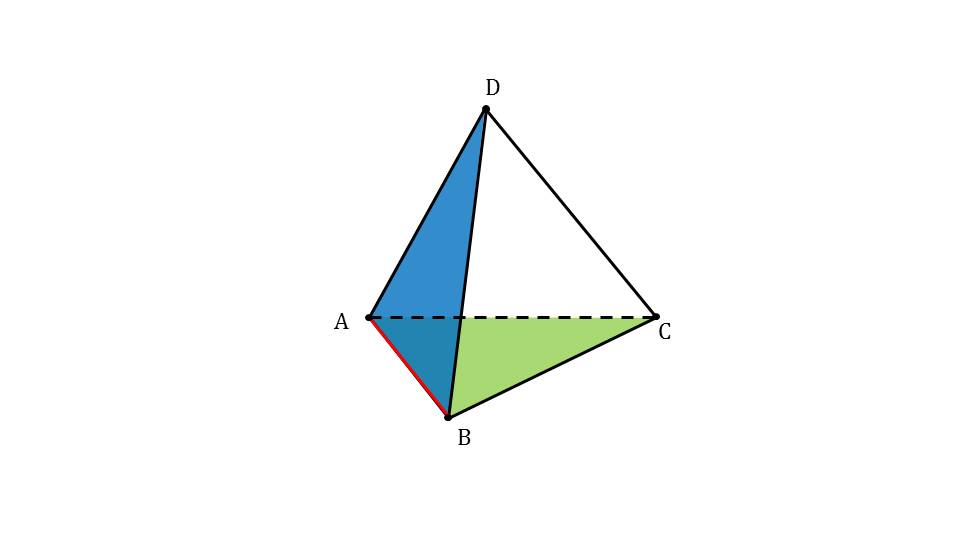
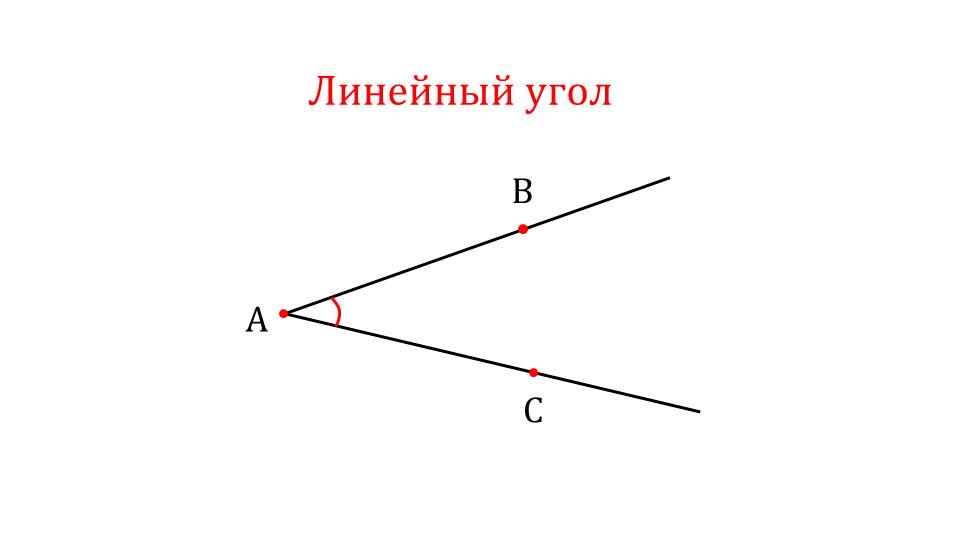
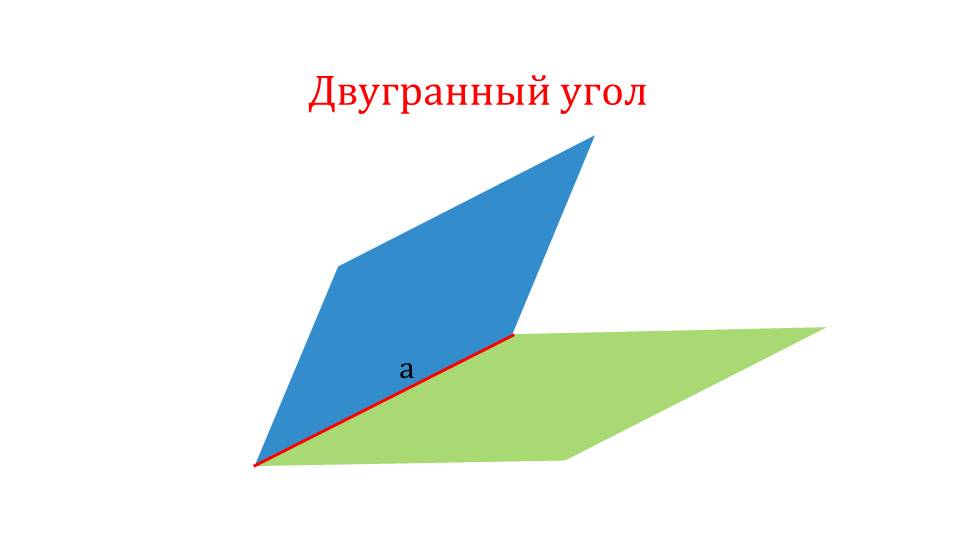
Презентация начинается с напоминания ученикам понятия линейного угла как угла, изображенного на плоскости. На рисунке изображен угол ∠АВС, обозначен сам угол. Над рисунком отмечено название понятия – линейный угол. Далее демонстрируется двугранный угол, который образуется двумя плоскостями, пересекающимися по некоторой прямой а. Над рисунком отмечается название понятия, выделенное цветом – двугранный угол. Демонстрируется двугранный угол, который образуют грани пирамиды. На рисунке изображается пирамида ABCD, в которой залиты цветом две грани ABD и ABC. Таким образом, в данной фигуре ученики могут узнать образованный двугранный угол.


Приводятся примеры двугранных углов, которые мы часто встречаем в окружающем мире. На слайде представлено фото «скамьи примирения», сидение которой состоит из двух частей, моделируя двугранный угол. Благодаря этому, если два человека садятся на скамью, они обязательно окажутся вплотную друг к другу. Представлено фото коттеджа, в котором двускатные крыши также представляют собой двугранный угол. Такая форма способствует эффективному отведению воды от дома.
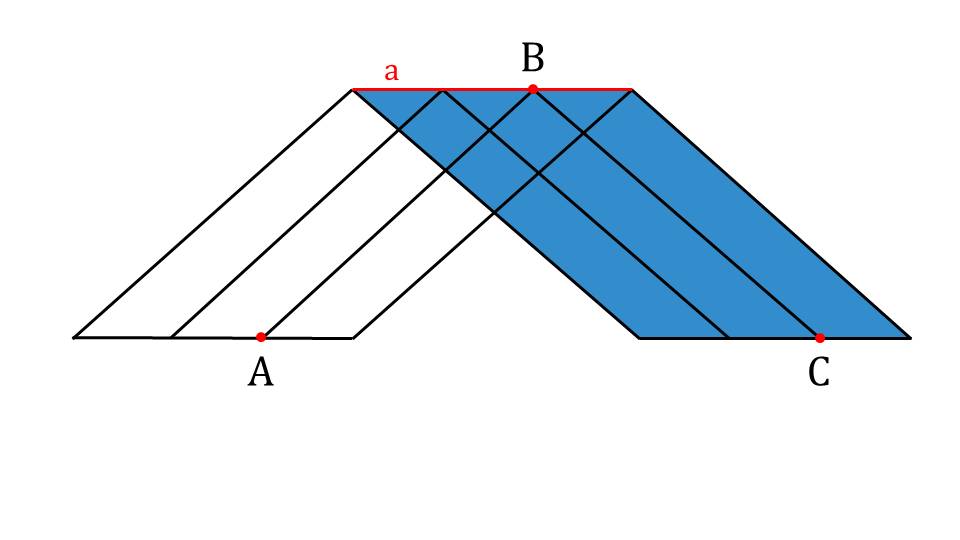

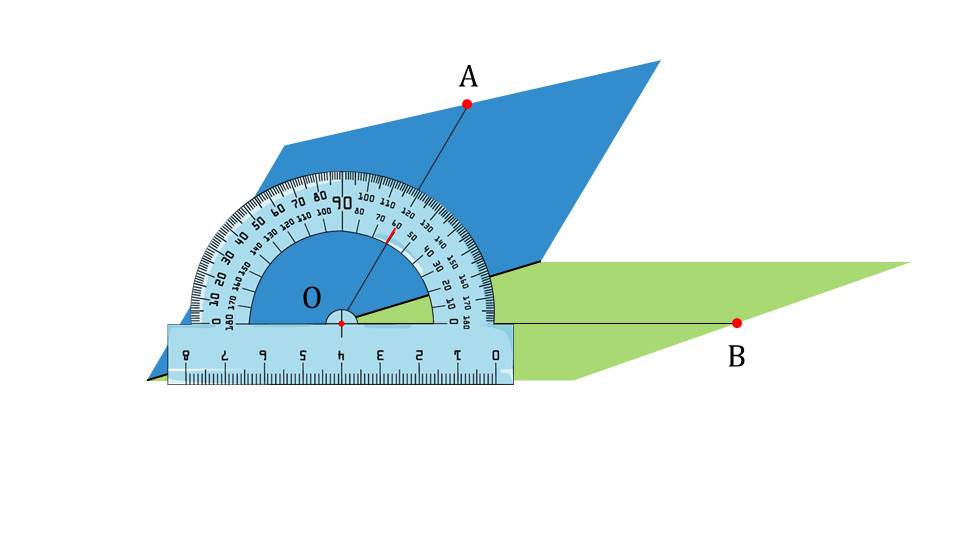
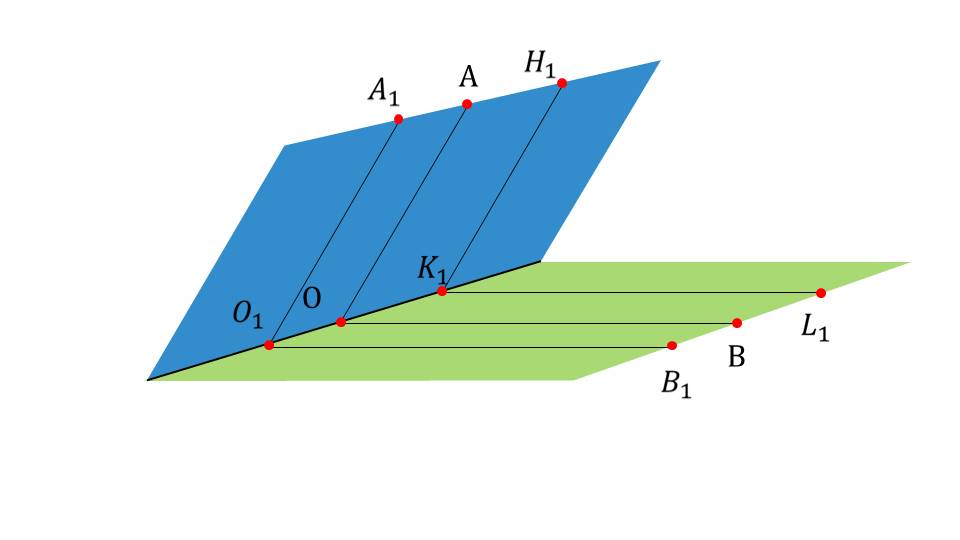
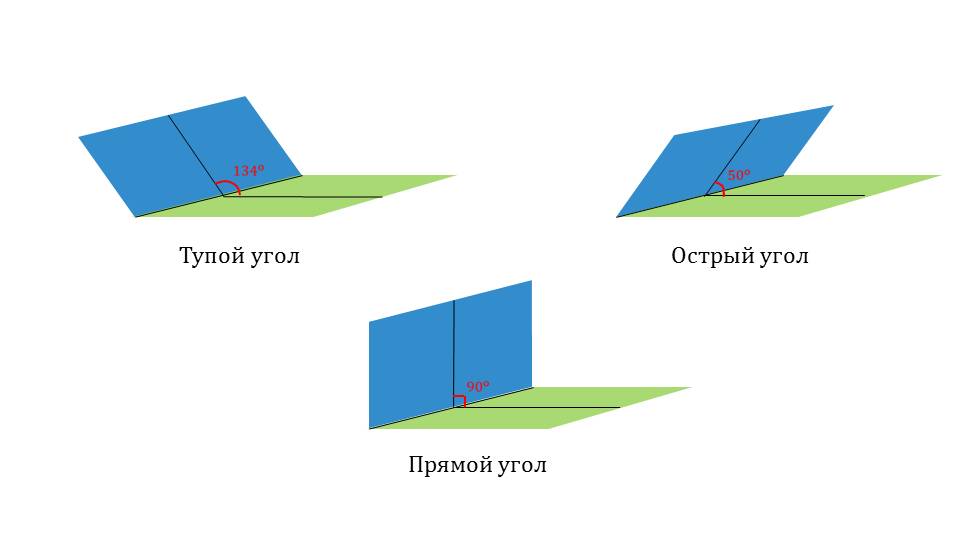
На следующем слайде представлено изображение двугранного угла, в котором проведено несколько линейных углов с параллельными соответствующими сторонами. Для представления выделен один из линейных углов ∠АВС. Представляется определение градусной меры двугранного угла как градусной меры его линейного угла. Определение выделено на отдельном слайде и может быть предложено к записи и запоминанию. Далее демонстрируется измерение линейного угла двугранного угла с помощью транспортира. На следующем изображен двугранный угол, в котором отмечены линейные углы ∠Н1К1L1, ∠АОВ, ∠А1О1В1,. Представлено, каким образом выглядят двугранные углы различных видов. Аналогично линейным, они бывают тупыми, острыми, прямыми. Вид двугранного угла определяется градусной мерой соответствующего линейного угла. На рисунке изображены: тупой двугранный угол величиной 134°, острый двугранный угол величиной 50°и прямой двугранный угол.
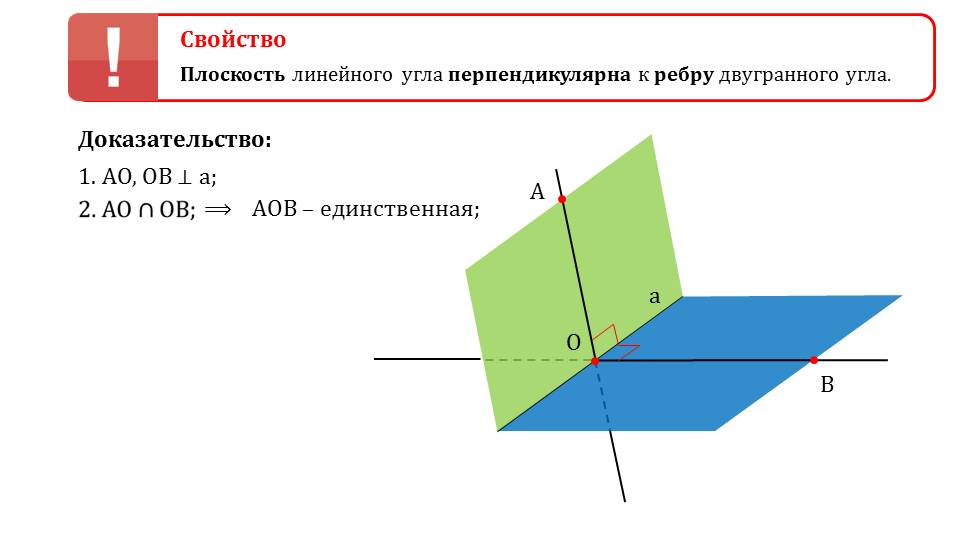
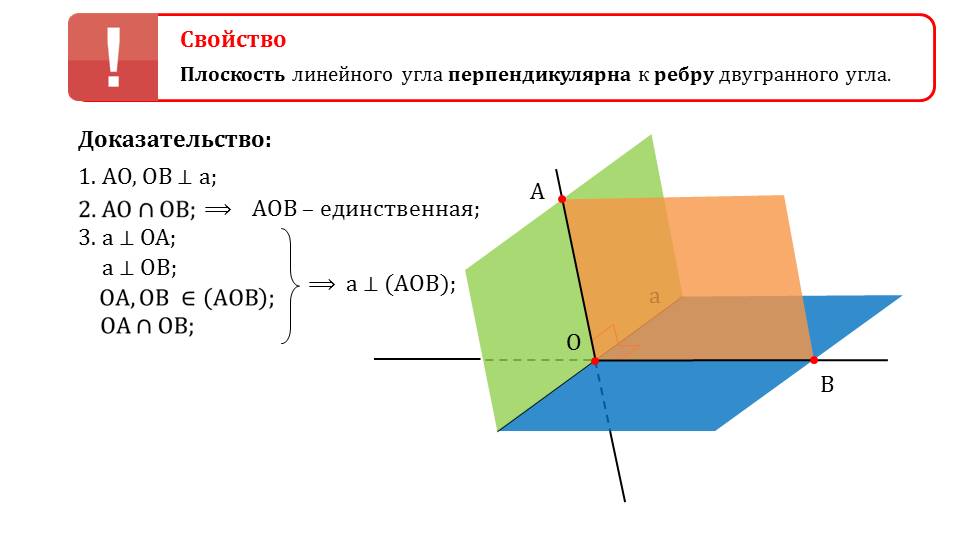
Далее доказывается свойство двугранного угла, в котором утверждается, что плоскость, которой принадлежит линейный угол, перпендикулярна к ребрам двугранного угла. Для доказательства свойства строится изображение двугранного угла, пересекающегося по прямой а. В нем отмечается соответствующие ему линейный угол ∠АОВ, в котором отмечено, что прямая ОА перпендикулярна прямой а и прямая ОВ перпендикулярна прямой а. Так как АО и ОВ пересекаются, существует единственная плоскость, включающая данный угол. А так как прямая а перпендикулярна АО и ОВ, то перпендикулярна и этой плоскости. Утверждение доказано.

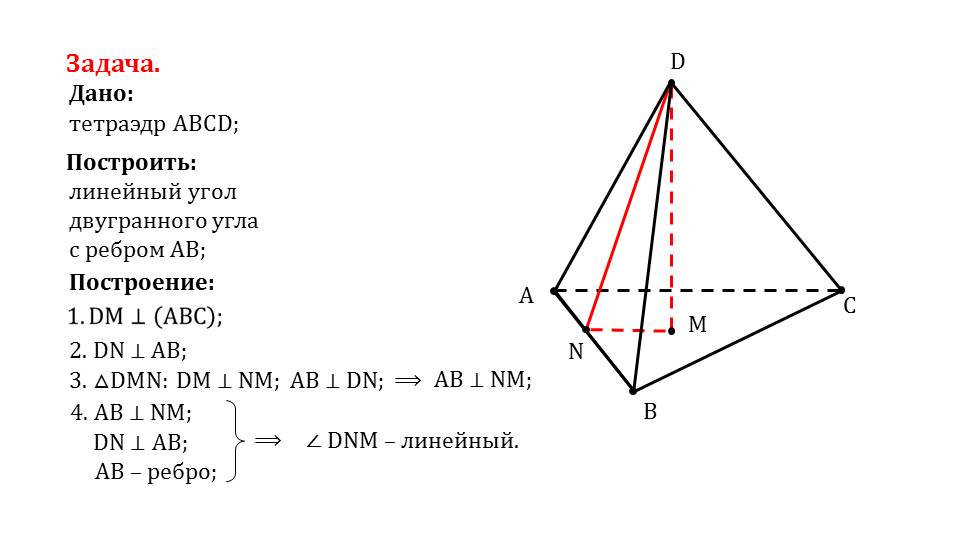
На следующем слайде рассматривается решение задачи, в которой дан тетраэдр ABCD. Необходимо выполнить задачу на построение – начертить линейный угол, соответствующий двугранному углу. Чтобы решить данную задачу, отмечается необходимость построить сначала высоту DM, которая представляет собой перпендикуляр, опущенный из вершины D на плоскость (АВС). Затем опускается перпендикуляр из точки D на ребро основания АВ. В треугольнике ΔDNM по построению очевидна перпендикулярность ребра АВ и отрезка NM. Из этого факта, а также из перпендикулярности DN и AB следует, что ∠DNM является линейным углом.
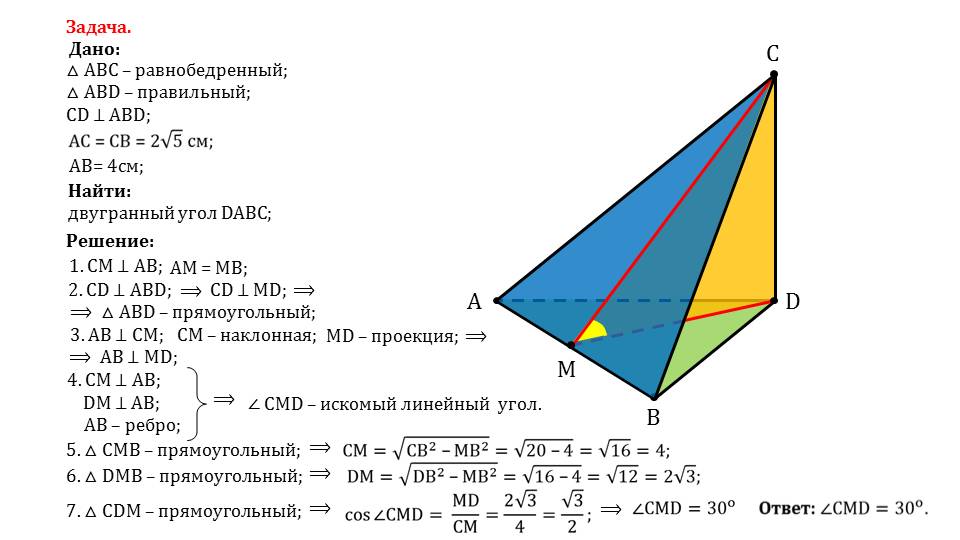
На последнем слайде описано решение задачи, в которой дан равнобедренный треугольник ΔАВС, правильный треугольник ΔАВD и проведенный из вершины С перпендикуляр к вершине D. Известно, что АС=СВ=2√5 см, а АВ=4 см. необходимо найти величину двугранного угла DABC. Решение сопровождается рисунком, на котором изображен тетраэдр, образуемый данными фигурами. Из вершины С на основание АВ треугольника ΔАВС опускается перпендикуляр СМ. Так как треугольник равнобедренный, перпендикуляр является высотой и делит АВ пополам. Из перпендикулярности CD следует и перпендикулярность CD к MD, поэтому ΔМВD является прямоугольным. Перпендикулярность наклонной СМ, проекции DM к ребру АВ свидетельствует о перпендикулярности АВ и MD. Учитывая этот факт, можно утверждать, что ∠CMD является искомым линейным углом. Используя свойства прямоугольных треугольников, находим длину отрезков СМ=√(СВ2-МВ2)=4 из треугольника ΔСМB, также из треугольника ΔDMB находим DM==√(DВ2-МВ2)=2√3, а из треугольника ΔСDМ находим cos∠CMD= DM/СМ=√3/2. Отсюда, величина угла ∠CMD=30°.
Презентация «Двугранный угол» предназначена для повышения эффективности традиционного урока геометрии в школе. Также материал может послужить наглядным пособием для ведения урока в ходе дистанционного обучения.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 9345 |
| Номер материала | 894 |