
Презентация "Элементы симметрии правильных многогранников"

Краткое описание документа:
Презентация «Элементы симметрии правильных многогранников» структурирует информацию о симметрии данных фигур. Ранее ученики ознакомились с понятиями симметрии в пространстве, узнали о видах многогранников и критериях определения правильных многогранников, изучили свойства многогранников. Чтобы данный материал усвоился лучше, автор приводит в данной презентации четкие и понятные рисунки. Презентация может использоваться учителем геометрии на уроке, когда чертить изучаемые фигуры на доске долго, тогда как показ слайдов предоставит время для более детального изучения и обсуждение возникших вопросов. Ученикам презентация поможет в случае необходимости самостоятельно подготовить урок.
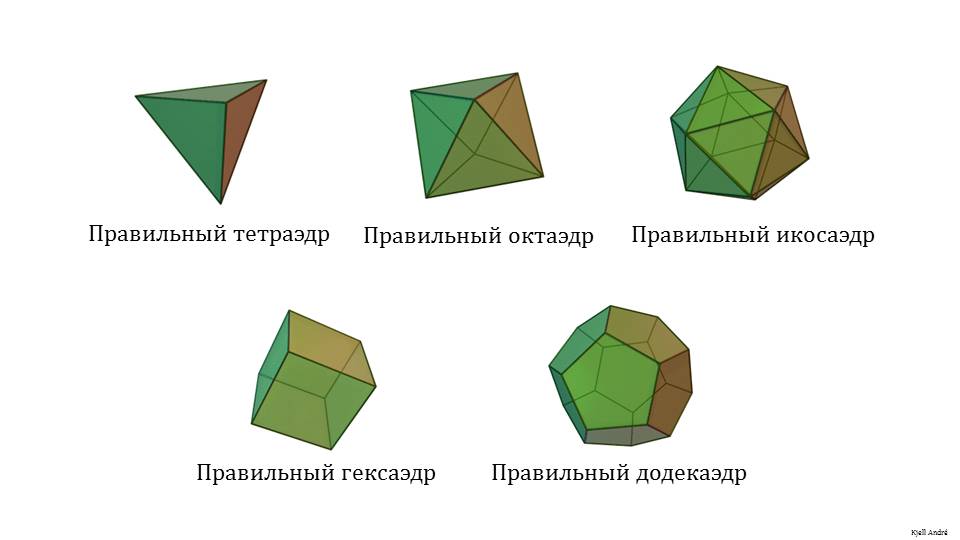
Просмотр первого слайда напоминает о видах правильных многогранников: тетраэдр, октаэдр, икосаэдр, гексаэдр, додекаэдр.
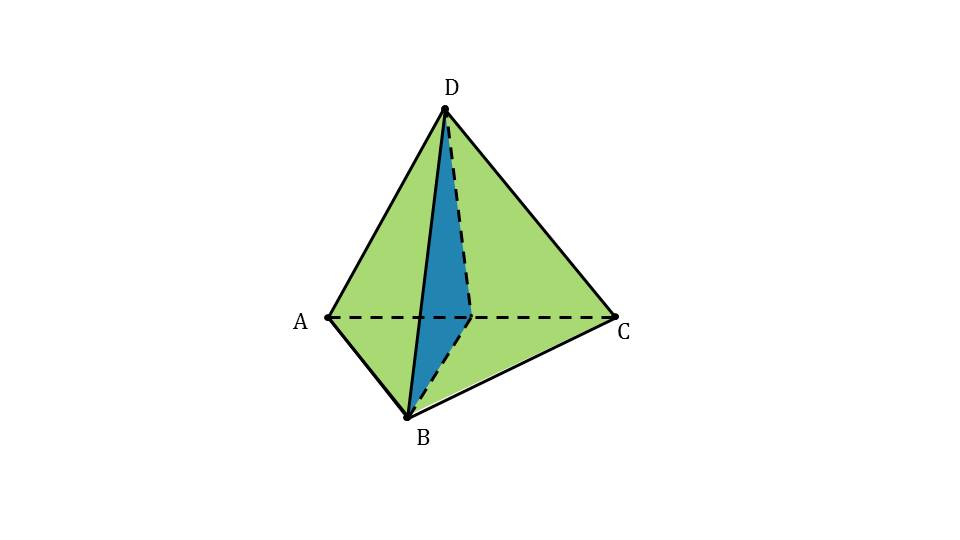
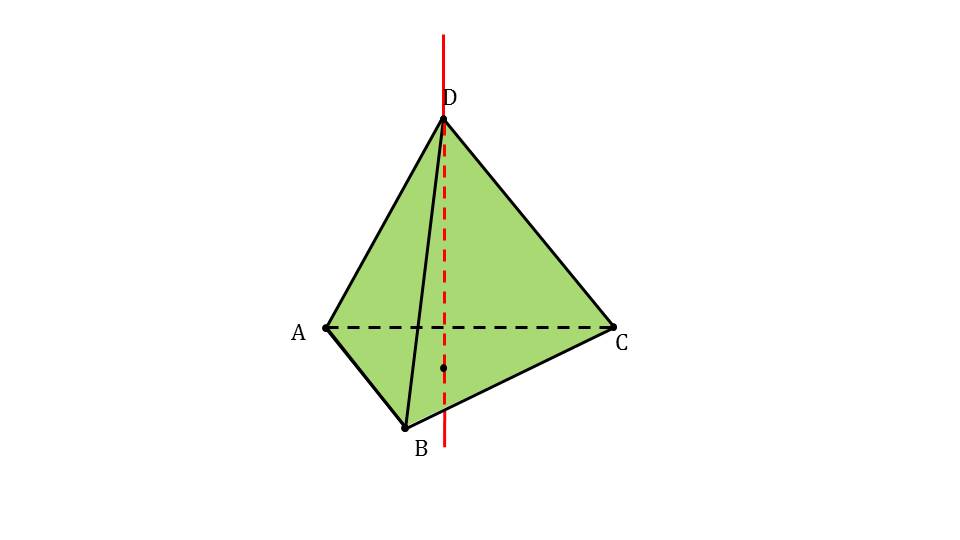
На слайдах 2 и 3 изображены симметрии тетраэдра:
- ось симметрии – прямая, проходящая через вершину тетраэдра и точку, которая является центром описанной окружности основания;
- плоскость симметрии, проходит через одно ребро и середину другого ребра.
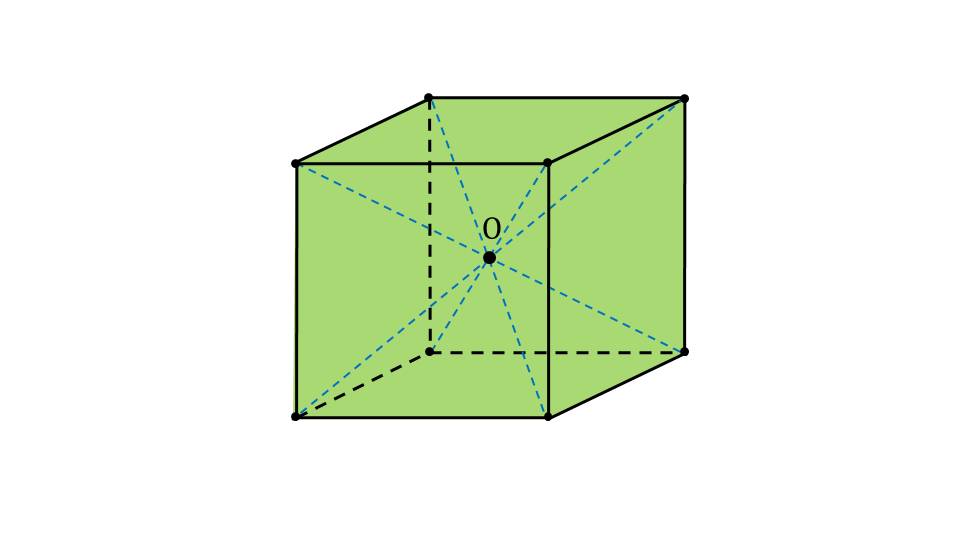
Далее показаны элементы симметрии куба:
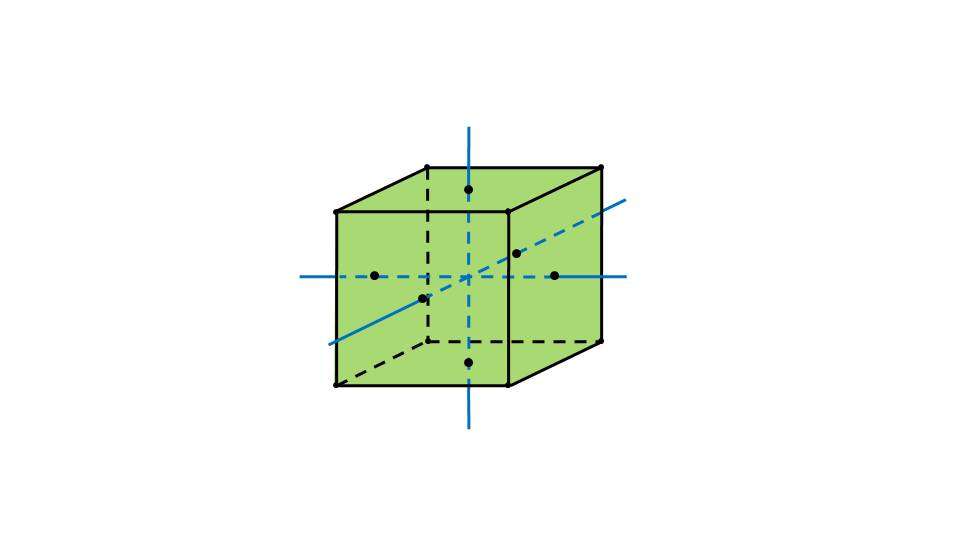
- оси симметрии – прямые, пересекающиеся в центре симметрии и проходящие через углы куба (слайд 4);
- оси симметрии – прямые, пересекающиеся в центре симметрии и проходящие через точки, которые являются серединами граней куба (слайд 5);
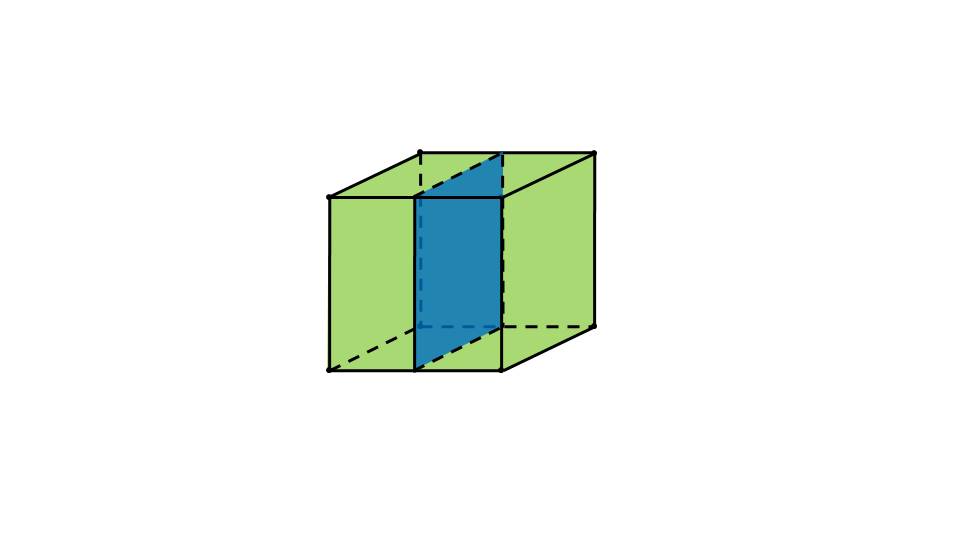
- плоскость симметрии (частный случай, слайд 6).
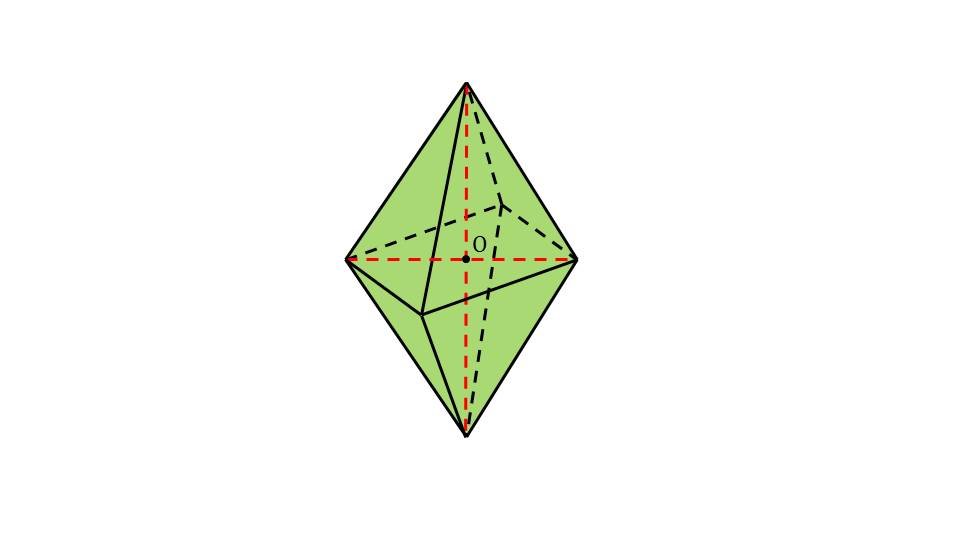
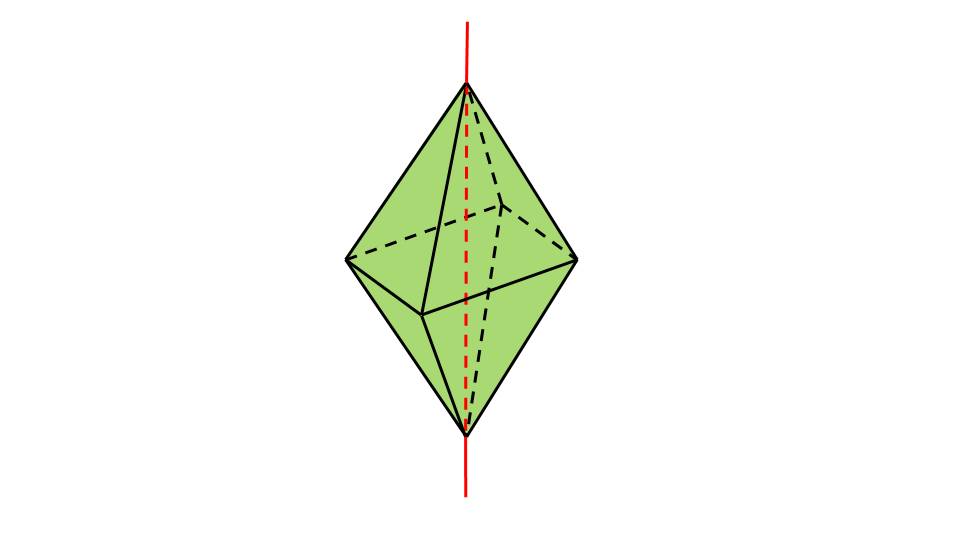
Рассматриваются также симметрии в правильном октаэдре. Слайд 7 иллюстрирует осевую симметрию правильного октаэдра, слайд 8 – симметрию плоскости правильного октаэдра.
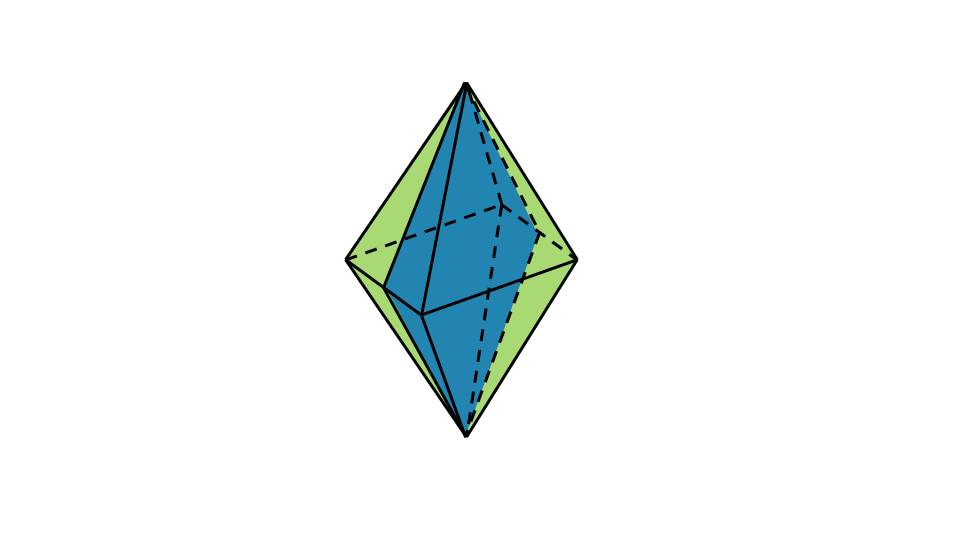
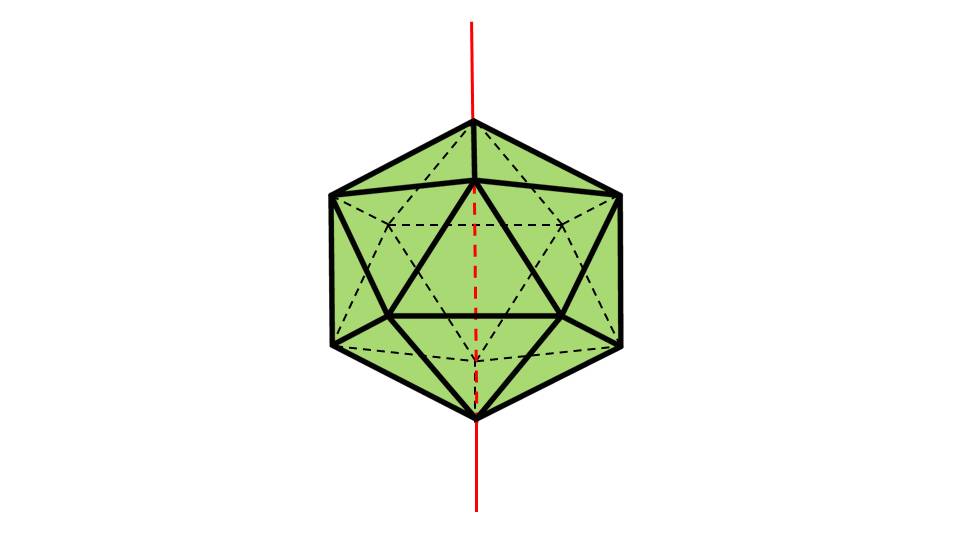
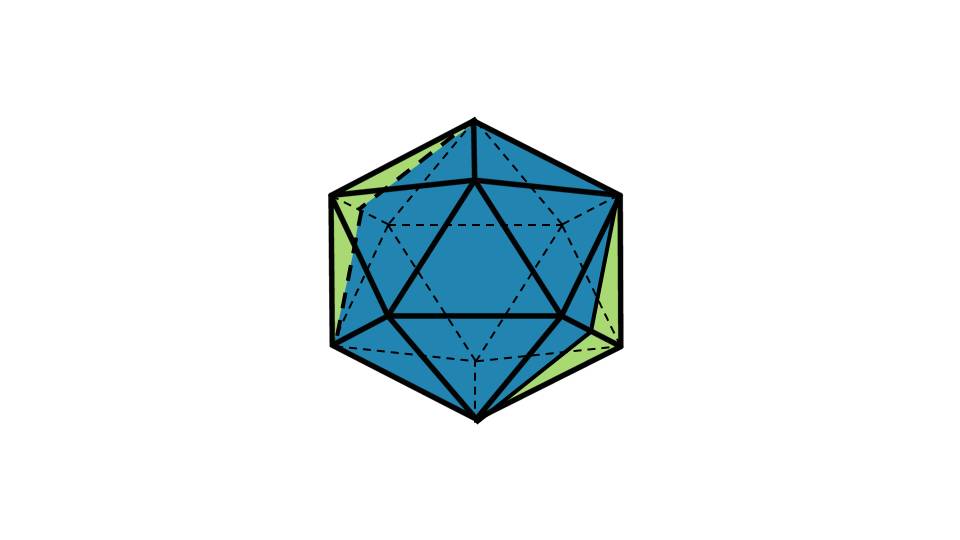
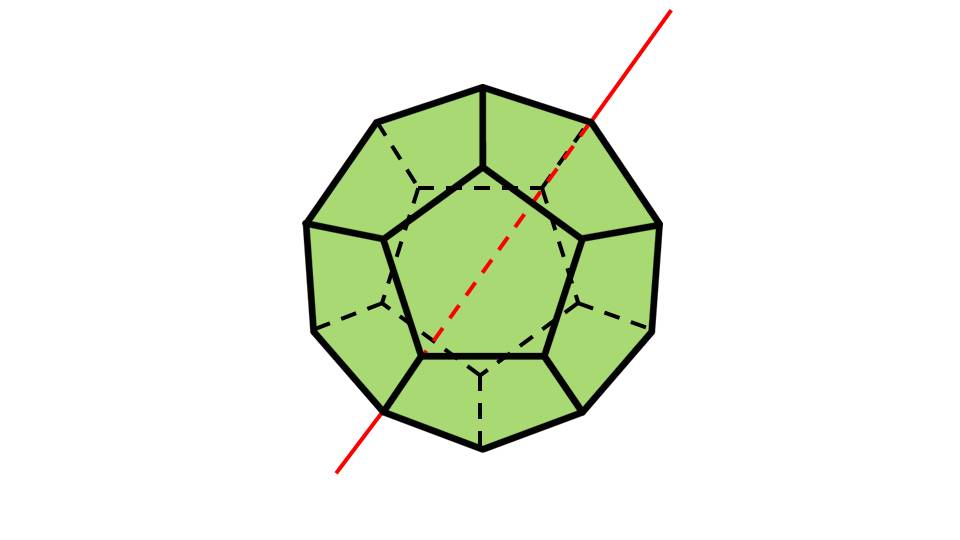
На 9-ом слайде презентации учащиеся видят икосаэдр – многогранник, состоящий из 20 равносторонних треугольников. На чертеже схематично изображена осевая симметрия икосаэдра. На следующих слайдах (10, 11, 12) показаны 2 вида элементов симметрии плоскости икосаэдра, и еще 1 вариант осевой симметрии.
После теоретической части автор приводит 2 задачи.
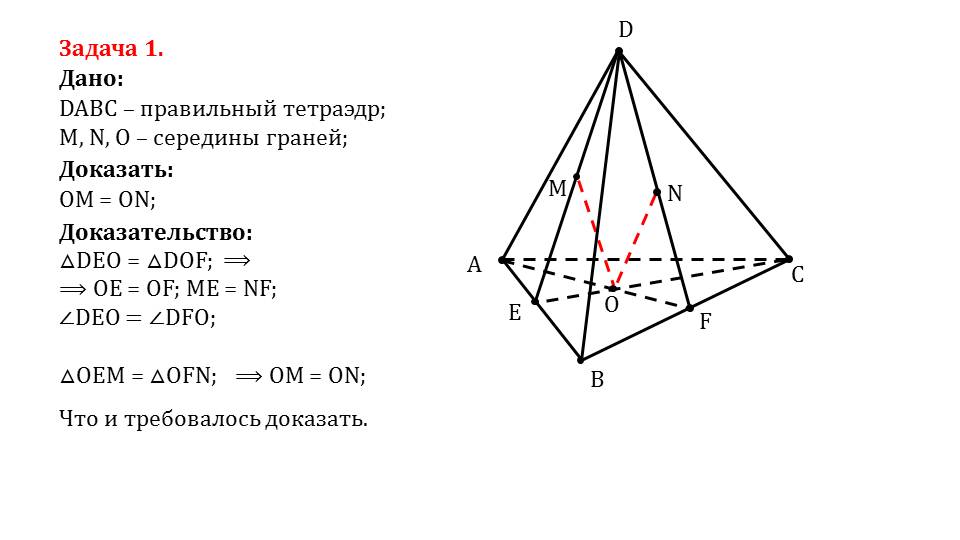
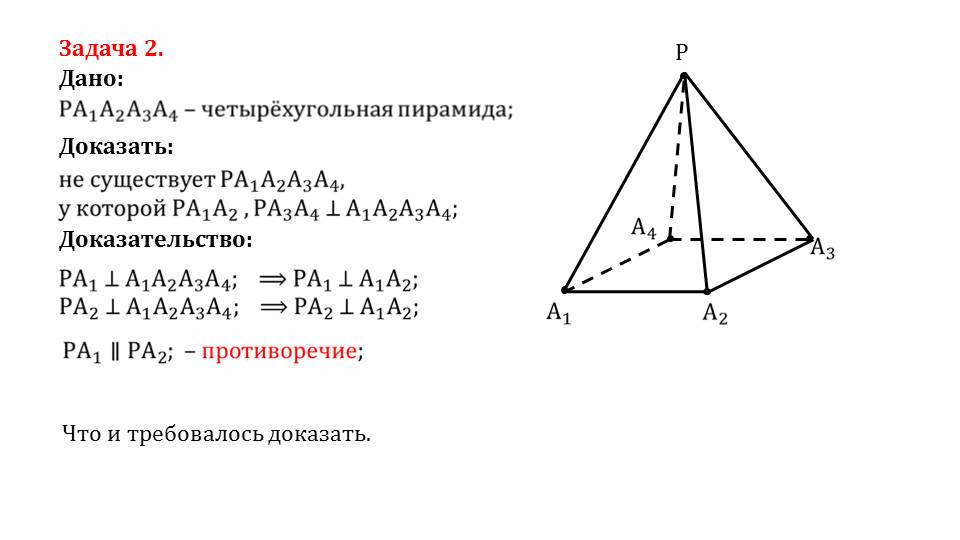
В задаче 1 дается многогранник – правильный тетраэдр; необходимо доказать равность определенных отрезков. В задаче 2 дается четырехугольная пирамида; необходимо доказать, что не существует такой четырехугольной пирамиды, чтобы ее грани были перпендикулярны основанию. В доказательствах используются знания о свойствах многогранников. Прорабатывая задачи, ученики могут повторить изученный материал, научиться применять его на практике.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 4963 |
| Номер материала | 906 |