
Презентация "Функция y=ax^2+bx+c, её свойства и график"

Краткое описание документа:
Презентацию «функция y=ax2+bx+c, её свойства и график» учитель может использовать для ознакомления с одним из видов функций: квадратичная. Учащиеся поймут, что такое данный вид функции, как строить характерный ей график, а также как определить вид графика, если обращать внимание на коэффициент и знак дискриминанта. На первоначальном этапе важно не просто определить все термины, но и выделить характерные функции свойства для того, чтобы с лёгкостью решать типовые задачи в алгебре.
Презентация достаточно объёмная, но содержит весь необходимый материал по теме, которая поможет учащимся познакомиться с теоретическим материалом и испытать на себе яркие практические примеры. Преподаватель поможет учащимся вспомнить основные сведения о квадратичной функции, описать её свойства, решить вместе с классом типовые задачи, анализируя все последовательные действия. Данное пособие наиболее эффективно для изучения темы квадратичной функции.


слайды 1-2 (Тема презентации "Функция y=ax2+bx+c, её свойства и график", квадратный трехчлен)
После презентации темы, учитель должен наглядно объяснить, чем является данный формат функции, поэтому важно вспомнить определение. Квадратичной выступает функция вида «y=ax2+bx+c», где коэффициент «а» не равен нулю. Графиком данной функции является парабола с вершиной в точке «х» нулевое и «у» нулевое.
Новая тема основана на анализе квадратного трехчлена, то есть именно из-за близости данной темы учащимся необходимо спросить у них, какие специфические названия имеет каждый коэффициент, почему старший не может равняться нулю, что такое полное и неполное уравнение, как выглядит парабола. Если ранее материал о квадратичном уравнении преподавался должным образом, то учащиеся с лёгкостью смогут ответить на поставленные вопросы.
Далее на презентации мы видим объяснение таких нюансов, как определение коэффициентов и понятие неполной функции. То есть необходимо ответы на вопросы проанализировать визуально.


слайды 3-4 (пример, теорема)
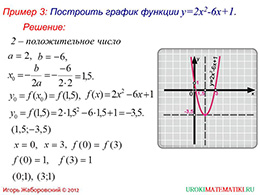
Рассмотрим первый пример, где старший коэффициент является отрицательным числом. Если выделить полный квадрат из функции, то мы увидим, что имеем дело с функцией, похожей на «y=ax2», только с дополнительными многочленами. Это означает, что графиком также является парабола, которую мы получаем при помощи параллельного переноса. В нашем случае ветви у функции направлены вниз, потому что старший коэффициент отрицателен.
Теперь проанализируем свойства нашей функции, в которой ветви направлены вниз:
- Область определения – все действительные числа.
- Область значения – «у» равен или меньше «у» нулевое.
- Функция возрастает, когда «х» принадлежит отрезку от минус бесконечности до «х» нулевое включительно.
- Функция убывает, когда «х» принадлежит отрезку от «х» нулевое включительно до плюс бесконечности.
- Наибольшее значение функции является значение «у» нулевое.
- Наименьшее значение функции не существует.
- Функция выпукла вверх.
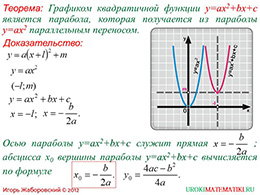
С учащимися решили конкретный пример, а теперь необходимо проанализировать теорему, формулировка которой доступна на слайде. Учащиеся уже вспомнили, что графиком данной функции выступает парабола. Она получается из графика «y=ax2» при помощи параллельного переноса. Именно это мы и попытаемся доказать.
После формулировки теоремы ниже представлено её доказательство, которое показывает метод выделения полного квадрата. Учитель должен проанализировать каждый шаг, объясняя сделанные изменения. В итоге мы получаем достаточно сложное уравнение и невозможно найти значения, не сделав несколько преобразований. В нашем случае новым преобразованием служит введение новых переменных «l» и «m», чтобы мы могли увидеть, как изменился формат уравнения.
В итоге мы видим, что график изначальной функции – парабола с параллельным переносом, а также выводим значение каждой переменной.

слайды 5-6 (теорема, пример)
Обратим вновь внимание учащихся на формулировку нашей теоремы, но теперь уже используем визуальное сопровождение, ведь эту же теорему мы можем доказать графическим путём. Вновь посмотрим на рисунок, где изображена функция «y=ax2» синим цветом, а розовым цветом мы видим новый график в виде параболы, которая получилась при помощи параллельного переноса.
В нашем случае осью параболы служит значение «х», то есть минус «b» разделить на два «а». Число «х» нулевое, являющееся абсциссой вершины нашей фигуры, равняется минус «b» разделить на два «а». Значение «у» нулевое или ординаты вершины нашего графика получается, подставляя значения «х» нулевое в изначальное уравнение.
Областью определения квадратичной функции является область определения всех действительных чисел, а на всей области определения график будет непрерывен.
Таким образом, мы с лёгкостью находим координаты вершины и знаем, чем является ось фигуры.
Старший коэффициент может быть числом как положительным, так и отрицательным. Однако само значение существенно влияет на свойство функции. Зная данную особенность, попробуем на следующем примере проанализировать график без построения его, а имея лишь данные уравнения.
Второй пример предлагает ответить на вопросы о том, что является осью параболы, где расположена её вершина, а также направление ветвей нашей фигуры.
Необходимо проанализировать каждый ответ, подтверждая верность или неверность ученика. На первый вопрос мы находим значение «х» и видим, что ось фигуры проходит через координату минус один. Далее мы высчитываем значение координат вершины. В конце концов, мы анализируем коэффициенты наших многочленов. Мы видим, что старший и средний коэффициенты являются отрицательными числами, поэтому, насколько нам уже известно, ветви нашей фигуры будут направлены вниз.

слайды 7-8 (примеры)
На следующем слайде необходимо более подробно остановиться на факте влияния старшего коэффициента на направление ветвей параболы функции. Следует подытожить, упоминая предыдущий пример, как коэффициент влиял на направление ветвей нашего графика (его отрицательное или положительное значение). Соответственно, при «а» меньше нуля, мы получаем направление ветвей вниз, а при «а» больше нуля – наоборот.
Для того чтобы доказать данное утверждение найдём значение "х". После этого мы знаем, что "х" нулевое – идентичное число, значит "х" нулевое равняется минус "b", поделённое на два "а". Значение "у" нулевое - это значение нашей функции, соответственно подставляем значение "х" нулевое в наше уравнение и получаем необходимое значение.
Подытожим: если коэффициент квадратичного многочлена больше нуля, то ветви нашего графика направлены вверх, а если старший коэффициент - отрицательное число, то ветви нашего графика направлены вниз.
Читаем график функции, анализируя иллюстрированные свойства.
Если аргумент возрастает от минус бесконечности до «х» нулевое, то функция убывает от минус бесконечности до «у» нулевое. Если аргумент возрастает от «х» нулевое до бесконечности, то функция возрастает от «у» нулевое до плюс бесконечности. Таким образом, «х» может меняться в пределах плюс/минус бесконечности, а «у» меняется в пределах «у» нулевое и плюс бесконечность. Следовательно, «у» нулевое выступает наименьшим значением функции, а наибольшего значения у функции нет.
Функция непрерывна, нет скачков. Это всё те сведения, которые нам даёт чтение заданного графика.
Теперь сформулируем свойства нашей функции:
- «х» принадлежит «R», то есть любое действительное число входит в область определения.
- Область значение – «у» больше либо равен «у» нулевое.
- Функция убывает, если «х» принадлежит промежутку от минус бесконечности до «х» нулевое, которое включается.
- Функция возрастает, если «х» принадлежит промежутку от «х» нулевое включительно до плюс бесконечности.
- Наименьшее значение существует, оно равно «у» нулевое. А вот наибольшего значения не существует.
- Функция выпукла вниз.
Таким образом, мы рассмотрели случай, когда коэффициент «а» больше нуля.

слайды 9-10 (алгоритм построения параболы, пример)
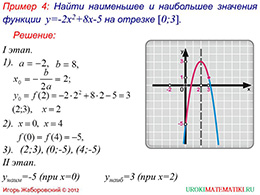
Теперь наиболее важным является проанализировать все этапы работы с квадратичным уравнением и процесс построения графика нашей функции.
Первым этапом в нашем алгоритме является процесс нахождения координат вершины нашей фигуры. Далее необходимо на координатной плоскости реализовать полученную точку. На втором этапе необходимо реализовать форму нашей фигуры, поэтому возьмём два дополнительных значения на оси абсцисс. После этого находим значение функции при таких значениях «х» и реализуем дополнительные точки. На завершающем этапе у нас есть все ресурсы для того, чтобы построить через точки функцию полученный график.
Таким образом, мы видим, что наша фигура симметрична относительно оси координат, её областью определения являются все действительные числа, а область значение, как и направление ветвей параболы, зависят от значений старшего коэффициента или «а».
Рассмотрим последний пример, где «а» меньше нуля, тогда графиком функции называется парабола, ветви которой направленны вниз. После нахождения всех корней, читаем график функции.
Если аргумент возрастает от минус бесконечности до «х» нулевое, то функция возрастает от минус бесконечности до «у» нулевое. Если аргумент возрастает от «х» нулевое до плюс бесконечности, то функция убывает от «у» нулевое до минус бесконечности. В данном случае функция развивает на отрицательно направленном луче.
Нам необходимо найти наибольшее и наименьшее значение на промежутке от нуля включительно до трёх включительно. Анализируем график и мы видим, что минимальное значение функции на промежутке минус пять, а максимальное – три.
Презентацию «функция y=ax2+bx+c, её свойства и график» можно использовать как сопровождение во время урока, используя предоставленное описание, как материал во время подготовки урока, или же, как материал для самостоятельного обучения данной теме.
| Автор | |
|---|---|
| Дата добавления | 30.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 12924 |
| Номер материала | 296 |