
Урок "Синус, косинус и тангенс острого угла прямоугольного треугольника"

Краткое описание документа:
Чтобы изучить основные термины и свойства такого важного раздела геометрии, как тригонометрия, необходимо тщательно отметить особенности прямоугольного треугольника, а также определения его элементов.
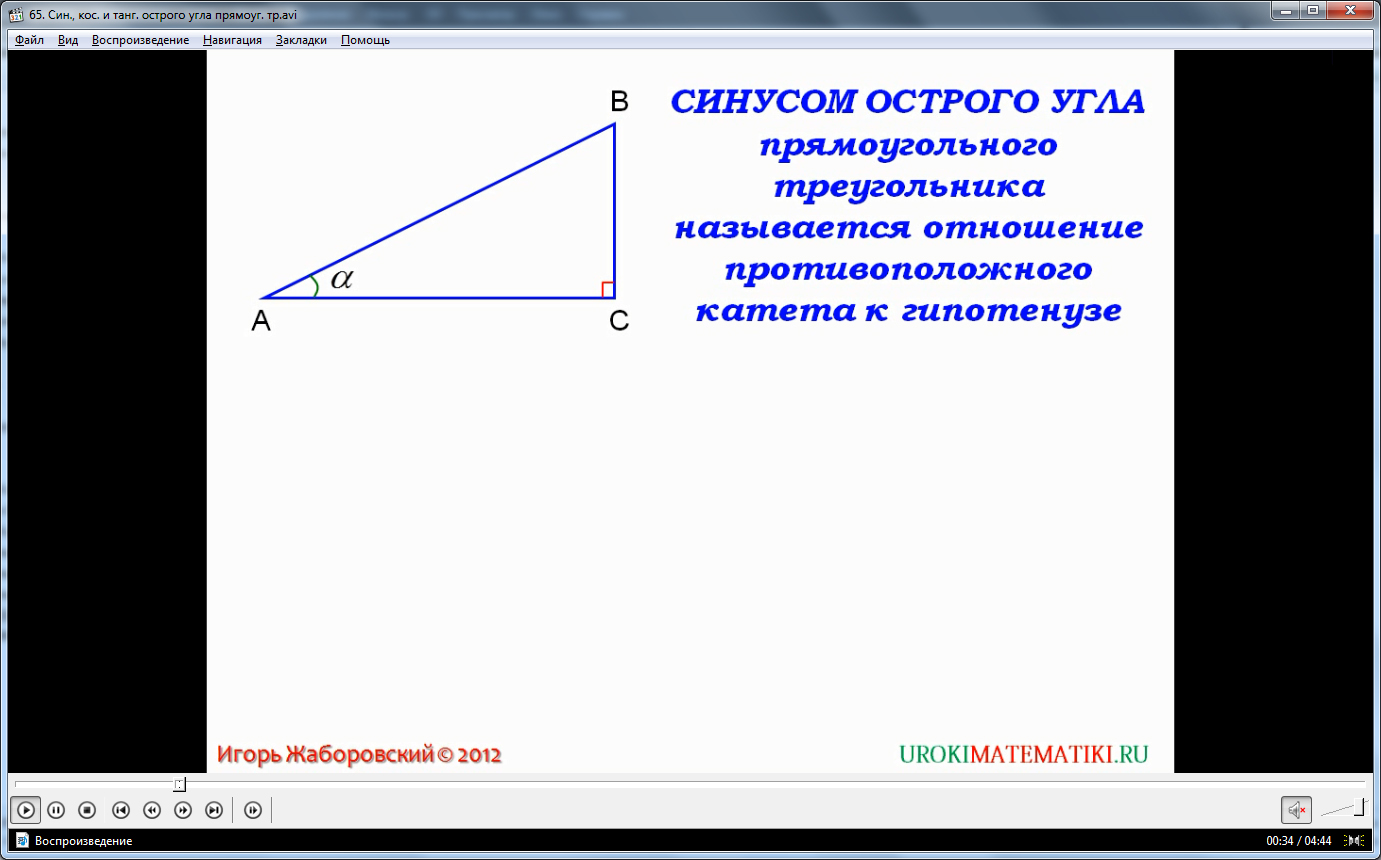
Прямоугольным называется треугольник, у которого один из углов равен 90 градусам, соответственно, сумма двух других равна 90 – из свойства всех треугольников об общей сумме углов. Обычно этот прямой угол обозначается буквой С. На видео представлен прямоугольный треугольник АВС с углом С = 90 градусов. Сторона, лежащая напротив прямого угла, именуется гипотенузой треугольника, а две другие стороны – его катетами. В нашем случае, АВ – это гипотенуза, а АС и ВС – катеты прямоугольного треугольника АВС.
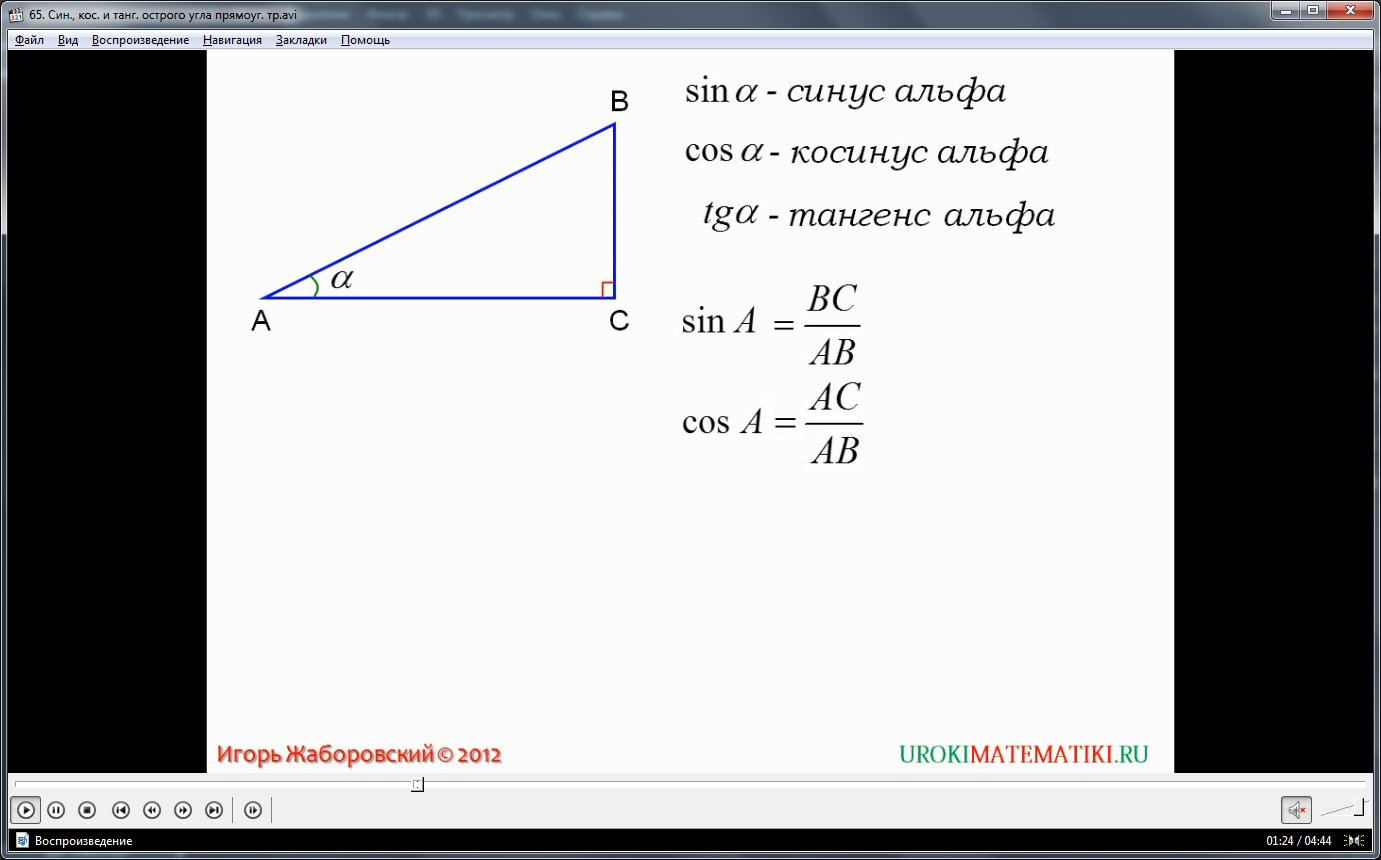
Главными тригонометрическими показателями являются синус, косинус и тангенс угла. Сразу же важно отметить, что эти понятия характеризуют абсолютно любой плоский угол по отдельности или в составе любого многоугольника. Однако, задаются они всегда через прямоугольный треугольник.
Синусом угла называется соотношение противолежащего катета к гипотенузе. Разумеется, если угол простой и отдельный, либо же является частью иной фигуры, синус задается только после дорисовки направляющих и образования полноценного прямоугольного треугольника. На представленной иллюстрации, sin АВС (В) = АС/АВ. Для вычисления синуса достаточно поделить линейные размеры отрезков, но их размерность в тригонометрии не имеет значения, поэтому, синус и все иные показатели этого ряда являются безразмерными значениями.
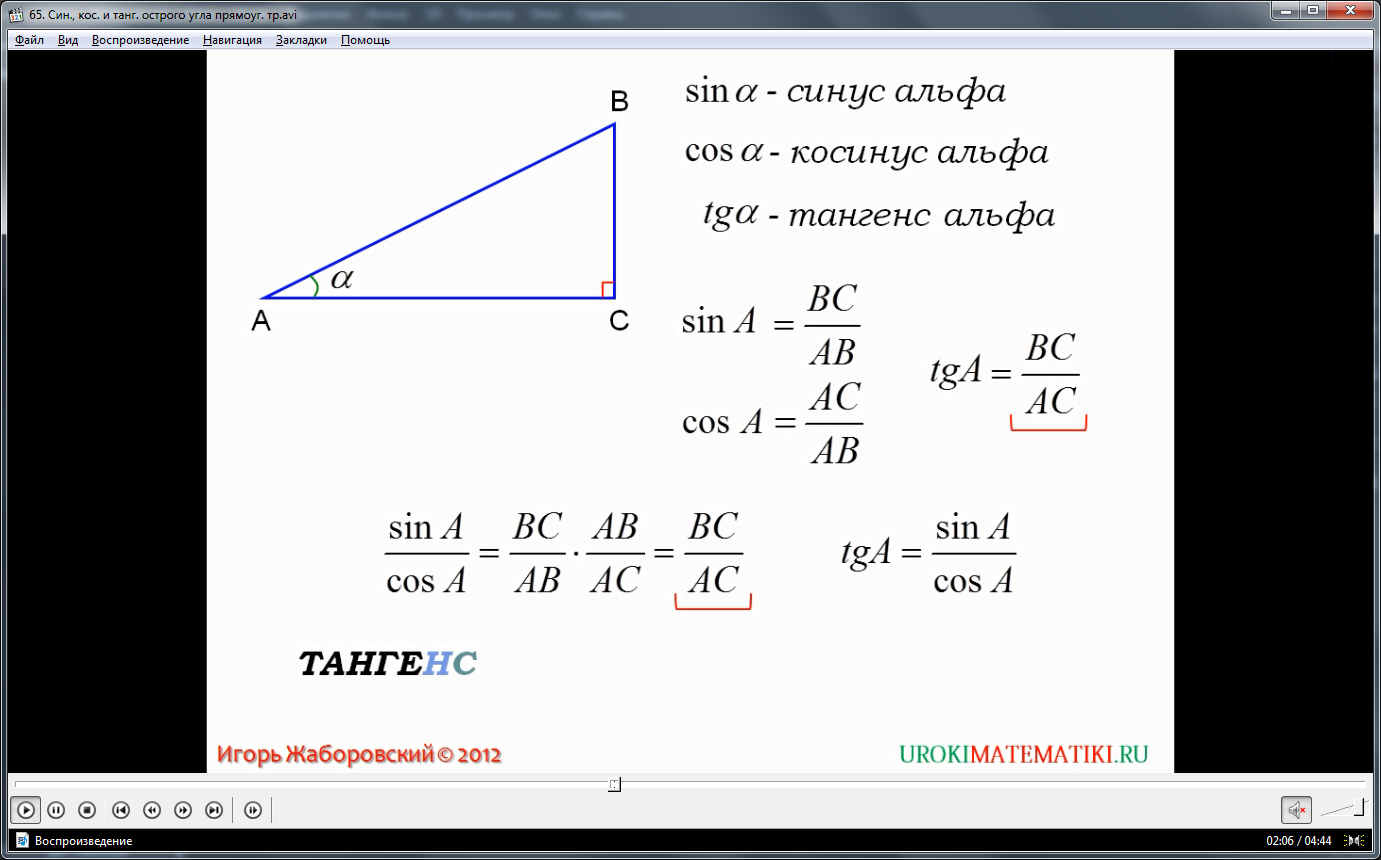
Косинусом угла называют соотношение прилежащего катета к гипотенузе. В нашем случае сos АВС (В) = СВ/АВ. Тангенсом угла называют соотношение противолежащего катета к прилежащему, т.е. tg АВС (В) = АС/СВ. Размерность и вычисления аналогичны таковым у синуса. Кроме того существует ещё понятие котангенса и нескольких других тригонометрических показателей, однако они все имеют второстепенную роль.
В нашем треугольнике АВС можно вычислить синус, косинус и тангенс для иного угла:
sin САВ (А) = СВ/АВ
cos САВ (А) = СА/АВ
tg САВ (А) = СВ/СА
Основное тригонометрическое равенство, которое мы рассмотрим более подробно, вытекает из определений синуса и косинуса, а также из знаменитой теоремы Пифагора. Для того, чтобы вывести тождество, необходимо вспомнить теорему прямоугольного треугольника: квадрат гипотенузы равен сумме квадратов катетов. Иначе говоря, АВ2 = АС2 + СВ2 для треугольника АВС при прямом угле С. Используя определения синуса, косинуса, и теорему Пифагора, получим для угла А:
sin В = АС/АВ
cos В = СВ/АВ
АВ2 = АС2 + СВ2
sin2 В + cos2 В = (АС/АВ)2 + (СВ/АВ)2 = АС2/АВ2 + СВ2/АВ2 = (АС2 + СВ2)/АВ2 = АВ2/АВ2 = 1
Таким образом, sin2 В + cos2 В = 1. Это и есть главное тригонометрическое тождество, которое можно обозначить в словесном виде: сумма квадратов синуса и косинуса одного угла равна единице.

Предположим, что у нас есть несколько прямоугольных треугольников разной величины, но при условии, что один из их углов равен у всех. Если у треугольника равны между собой два угла, то равен и третий (по свойству постоянной суммы углов), а сами треугольники являются подобными между собой. У подобных треугольников, по определению, стороны соотносятся пропорционально. Эта пропорция сохраняется и в соотношениях для определения тригонометрических показателей. Поэтому синус, косинус, тангенс и другие показатели тригонометрии равны для любого прямоугольного треугольника, да и вообще, являются постоянной характеристикой. Значения эти зависят исключительно от градусной меры самого угла.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 8795 |
| Номер материала | 603 |