
Презентация "Значение синуса, косинуса и тангенса для углов 30, 45 и 60 градусов"

Краткое описание документа:
Вводный урок по тригонометрии был представлен в предыдущей презентации. Школьники ознакомились с понятиями синус, косинус и тангенс, как они обозначаются, как их находить. Рассматривался острый угол некоторого прямоугольного треугольника. Также, они ознакомились с основным тригонометрическим тождеством, что составляет основу для многочисленных формул, с которыми ученики ознакомятся несколько позже.
Данный урок предлагает рассмотреть определенные углы: 45, 30 и 60 градусов. Необходимо найти их синус, косинус и тангенс. Все эти три угла являются острыми. Подразумевается, что мы работаем с прямоугольными треугольниками, как и в предыдущем уроке.

слайды 1-2 (Тема презентации "Значение синуса, косинуса и тангенса для углов 30, 45 и 60 градусов", пример)
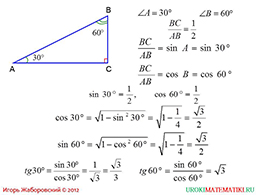
Первый слайд презентации «Значение синуса, косинуса и тангенса для углов 30, 45 и 60 градусов» продемонстрирует учащимся некоторый прямоугольный треугольник, острый угол которого равен 30 градусов. Зная о том, что один из углов является прямым, можем легко вычислить значение третьего угла. Сумма всех углов любого треугольника составляет 180 градусов. Об этом свойстве ученики восьмого класса уже должны знать. Итак, для того, чтобы найти третий неизвестный угол, необходимо отнять от 180и градусов 120 градусов, что составляет сумму остальных двух сторон. Третий неизвестный угол равен 60 градусов. Это отмечено на чертеже.
Автор отмечает, что отношение катетов прямоугольного треугольника ABС равно одной второй. Откуда автор получил такое число? Дело в том, что катет, который лежит напротив угла 30 градусов, что можно увидеть на рисунке, равняется половине гипотенузы данного треугольника. Это является одним из важных свойств прямоугольных треугольников. Данное отношение является синусом угла 30 градусов. Таким образом, синус угла 30 градусов найден.
слайды 3-4 (пример, таблица синусов, косинусов, тангенсов)
Данное отношение является также и косинусом для угла прилежащего к катету, то есть для угла 60 градусов. Далее, исходя из информации, которая была получена на предыдущем уроке, можно посчитать оставшийся тангенс, поделив найденный синус определенного угла на найденный косинус того же угла.
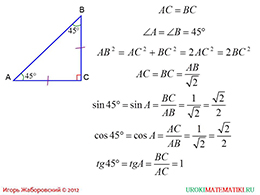
Следующий слайд аналогичным образом исследует синус, косинус и тангенс угла 45 градусов. Для начала находится третий неизвестный угол. Выясняется, что углы при гипотенузе равны, то есть треугольник, помимо того, что является прямоугольным, еще и равнобедренный. По теореме Пифагора выразим гипотенузу через катеты. Так как они равны, как выяснилось, то можно заменить один катет другим и получить простое произведение числа 2 на квадрат одного из катетов. Далее, автор избавляется от иррациональности и выражает катет. Таким образом, находятся два катета. Далее, пользуясь изученными формулами можно найти и синус, и косинус, и тангенс угла 45 градусов.
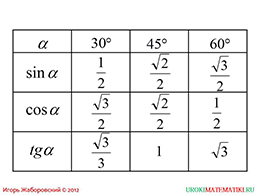
На последнем слайде приводятся данные значения в виде таблицы. Желательно, чтобы школьники записали таблицу себе с тетради. Можно сказать, она является аналогом таблицы умножения, только тригонометрическая. Желательно, чтобы школьники знали о том, откуда появились данные значения и запомнили таблицы.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 16587 |
| Номер материала | 347 |