
Презентация "Компланарные вектора"

Краткое описание документа:
Презентация – это удобный вид представления информация на уроке. Презентация содержит необходимые теоретические аспекты темы, наглядные рисунки, задачи. Такая структура позволяет ученикам с легкостью усваивать новый материал.
Данная презентация знакомит учащихся с таким новым понятием о векторах, как компланарность. Изучение данной темы предполагает, что ученики уже знакомы с определением вектора, его видами, знакомы с операциями сложения, вычитания и умножения векторов.
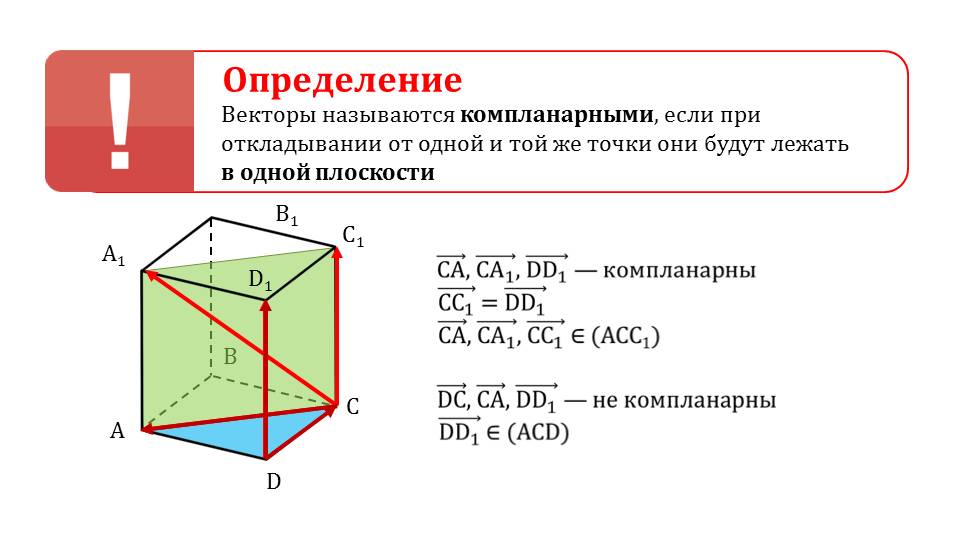

В начале презентации дается следующее определение: векторы, которые лежат в одной плоскости и отложены от одной точки, называются компланарными. В качестве примера на рисунке на слайде 2 представлен куб, в котором можно увидеть компланарные векторы и некомпланарные векторы, определить различия между ними. Отображены математические записи. На следующем слайде выделены положения, касающиеся компланарности векторов:
- любые два вектора являются компланарными;
- если из трех векторов два вектора коллинеарны, то все три вектора являются компланарными;
- три вектора могут быть как компланарными, так и некомпланарными (векторы расположены на плоскости произвольно).
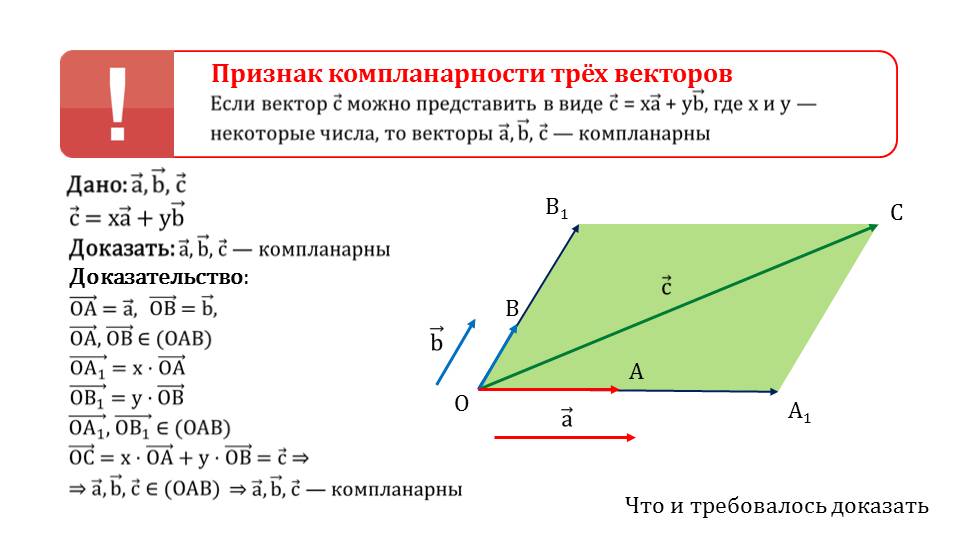

Эти утверждения необходимо запомнить, так как они будут использоваться при решении задач. Приводится признак компланарности трех векторов. Это утверждение требует доказательства, поэтому на слайде 4 школьники видят доказательство признака, соответствующе проиллюстрированное.
Следующий слайд (5) обращает внимание учеников, что существует утверждение, обратное признаку компланарности векторов.
Далее идет практическая часть презентации, это 2 задачи. В задачах дается параллелепипед и необходимо выяснить, являются ли заданные векторы компланарными или нет. Формируя у учеников способность делать логические рассуждения, учитель в ходе доказательств показывает, что в результате решения первой задачи искомые векторы являются компланарными, а во второй задаче – некомпланарными. Провести доказательства в задачах ученики могут и сами, используя изученные понятия о компланарности.
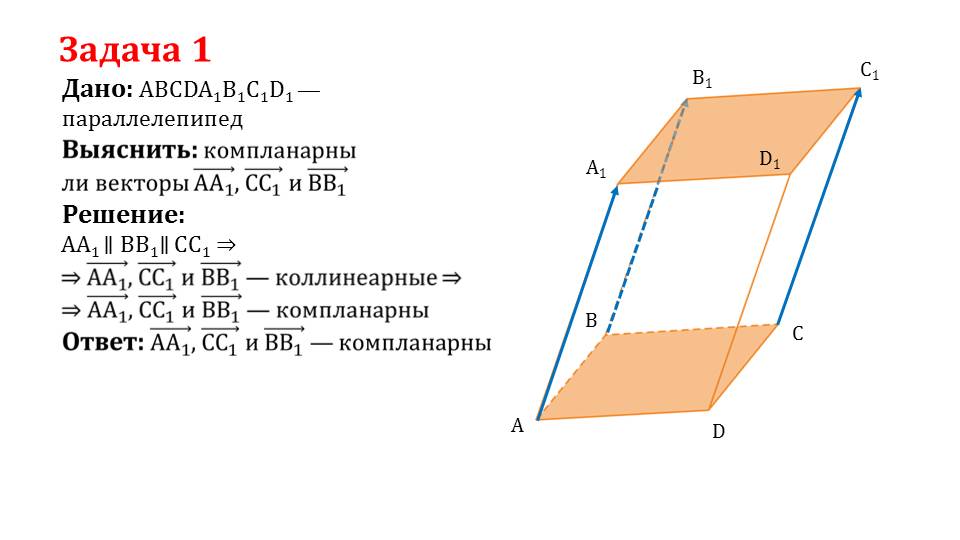
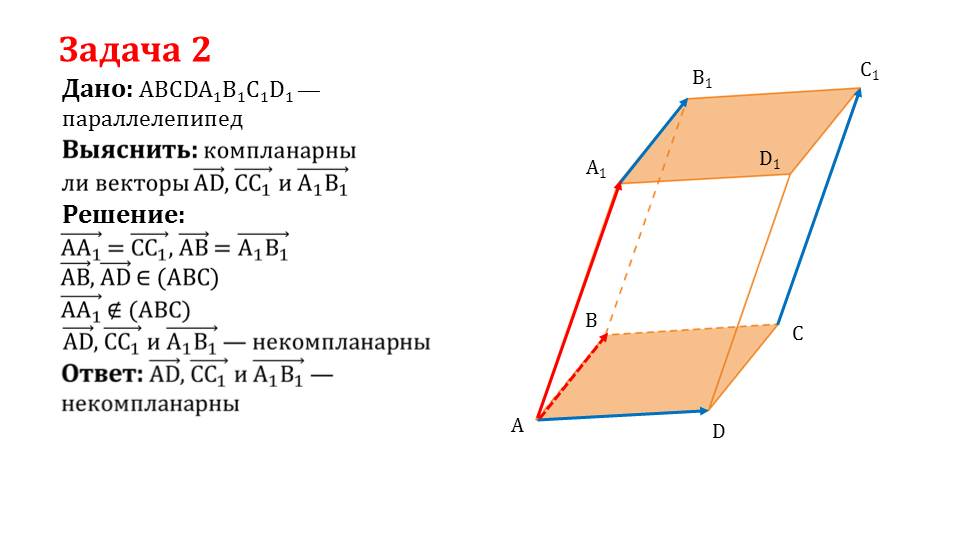
Решение задач позволяет применить на практике вновь полученные знания, а также помогает определить учителю, насколько хорошо усвоен материал учащимися.
Учитель может с легкостью использовать презентацию «Компланарные вектора» при подготовке к данному уроку, а также может дополнить презентацию другими заданиями, которые охватят несколько тем о векторах.
Ученики по презентации смогут изучать материалы самостоятельно.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 12941 |
| Номер материала | 912 |