
Презентация "Многогранники. Понятие правильного многогранника"

Краткое описание документа:
Данная презентация рассматривает следующую тему по программе стереометрии «Многогранники. Понятие правильного многогранника».
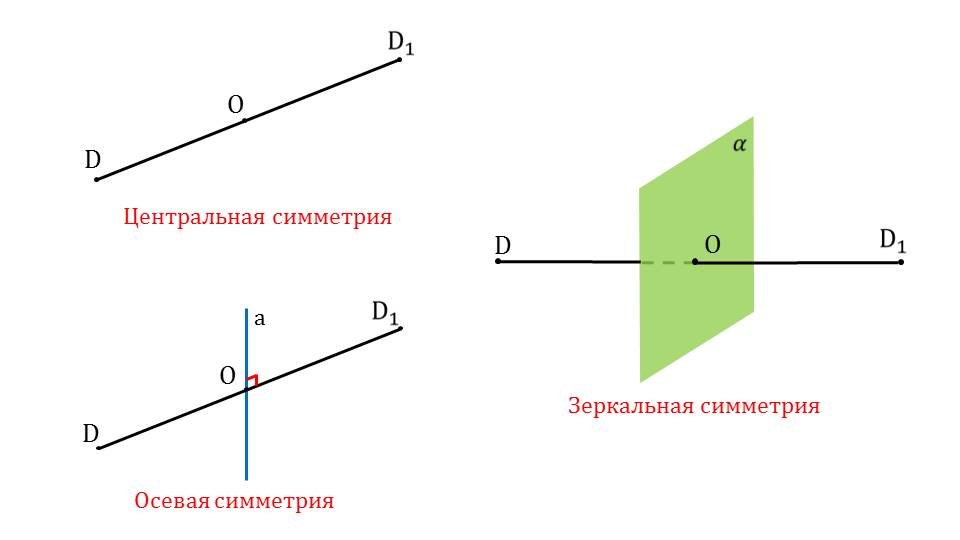

В начале презентации проиллюстрированы понятия центральной и осевой симметрии, с которым ученики уже знакомы, а также понятие зеркальной симметрии. Дается определение правильного многогранника. Частные случаи правильных многогранников: куб (слайд 3), тетраэдр, октаэдр, икосаэдр и другие.
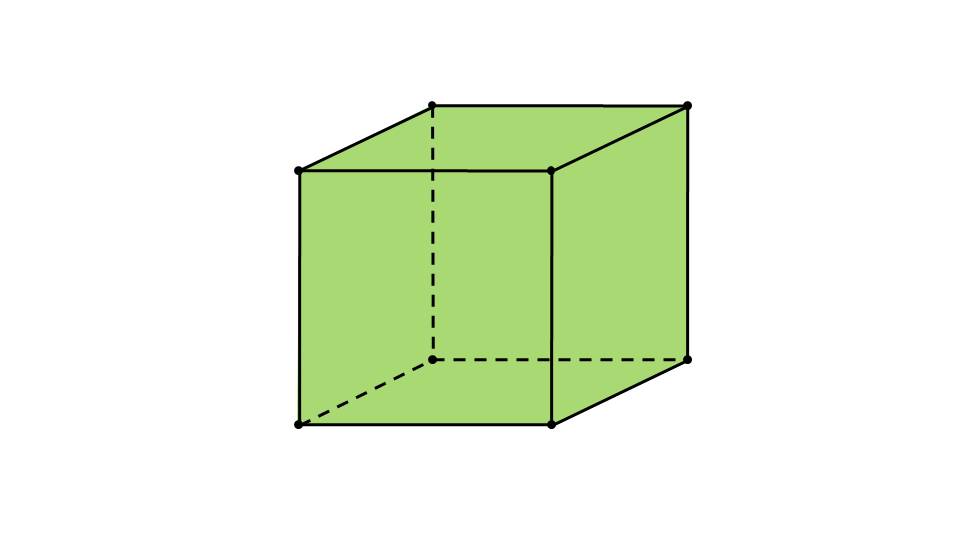

На слайде 4 делается акцент на следующем:
- в правильном многограннике все углы, которые являются двугранными и содержат две грани с общим ребром, равны;
- в правильном многограннике все ребра равны между собой. Эти свойства выделены тезисно, чтобы учащиеся могли лучше запомнить данные особенности изучаемых фигур.



Приводится утверждение с доказательством, что не существует такого правильного многогранника, чтобы его гранями были правильные n-угольники при n≥6.
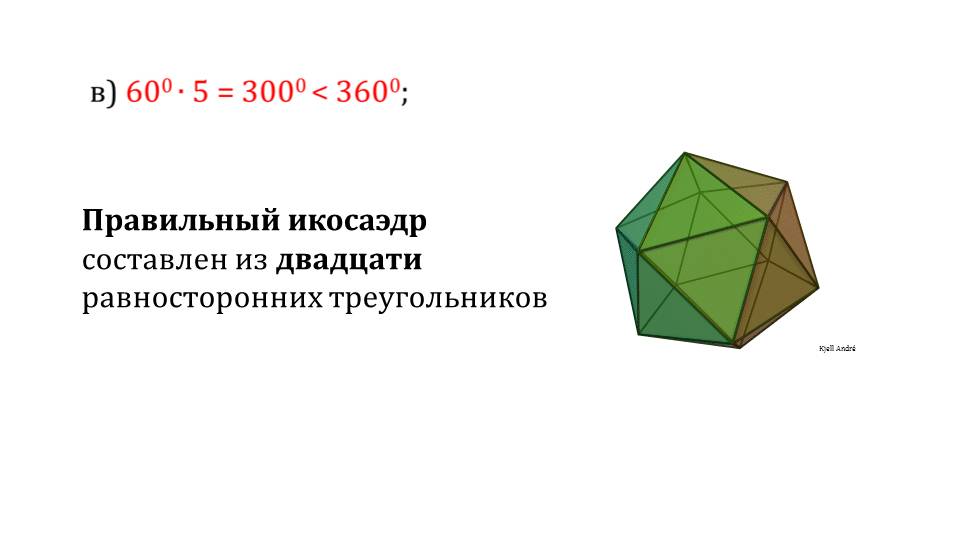


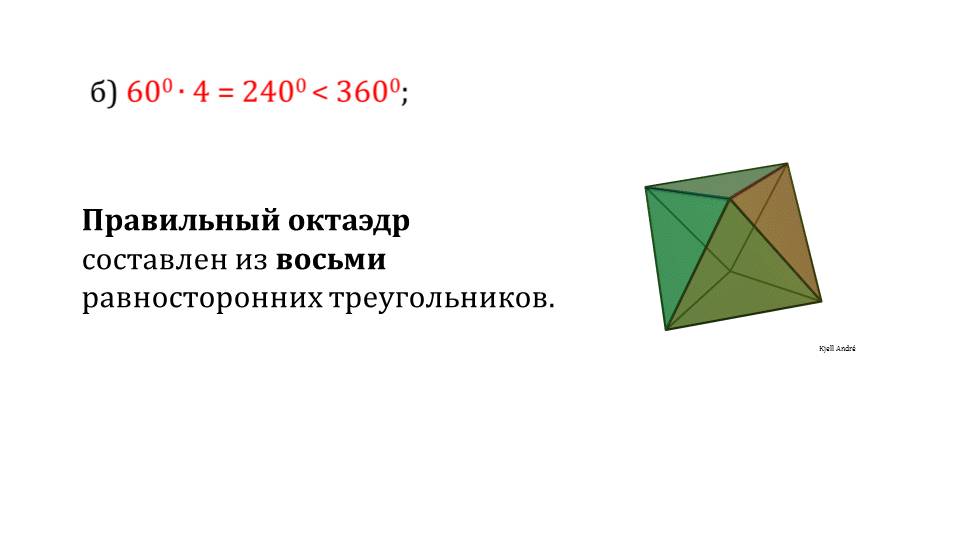
Последовательно рассматриваются правильные многогранники, которые состоят из равносторонних треугольников: правильный тетраэдр (слайд 7), правильный октаэдр (слайд 8), правильный икосаэдр (слайд 9). В описании используется свойство выпуклого многогранника, которое говорит о том, что сумма всех плоских углов при каждой вершине многогранника менее чем 360°.


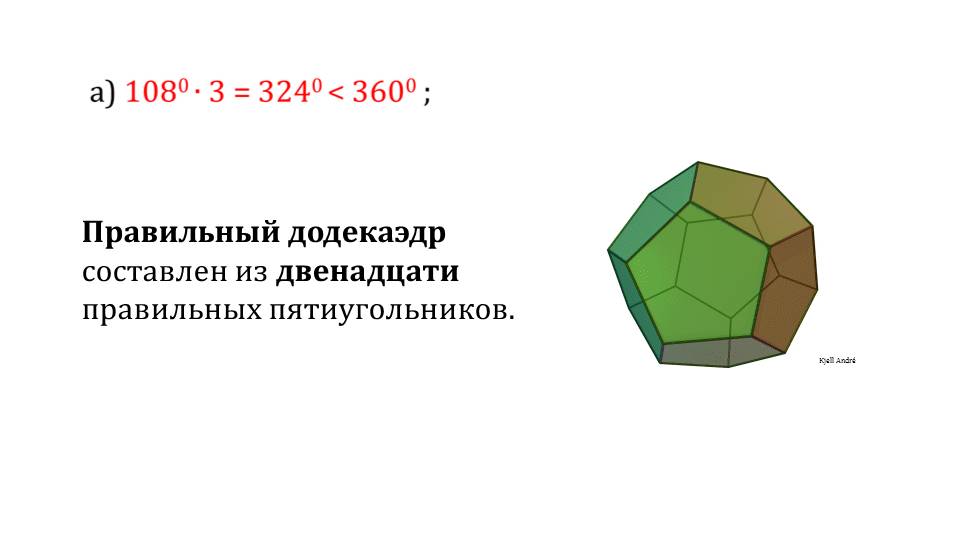
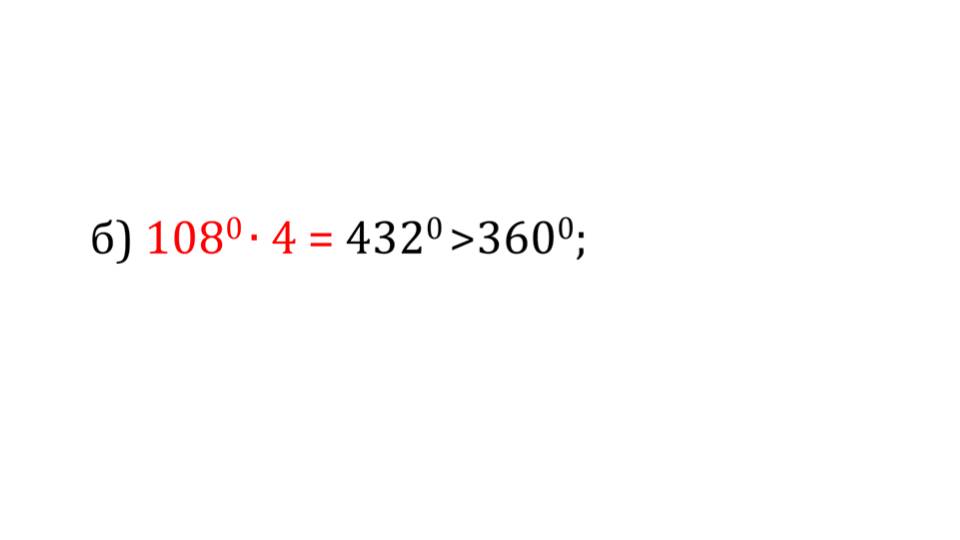
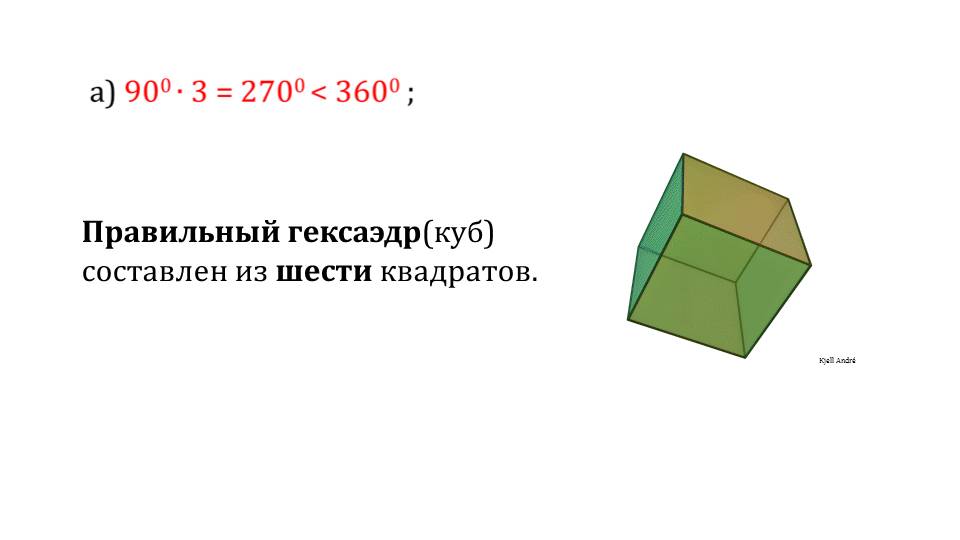
Аналогично рассматриваются правильные многогранники, которые состоят из правильных четырехугольников. Пример - правильный гексаэдр (куб, слайд 12). Также проиллюстрированы правильные многогранники, которые состоят из правильных пятиугольников. В качестве примера на слайде 15 изображен додекаэдр. Этот многогранник составлен из двенадцати правильных пятиугольников.

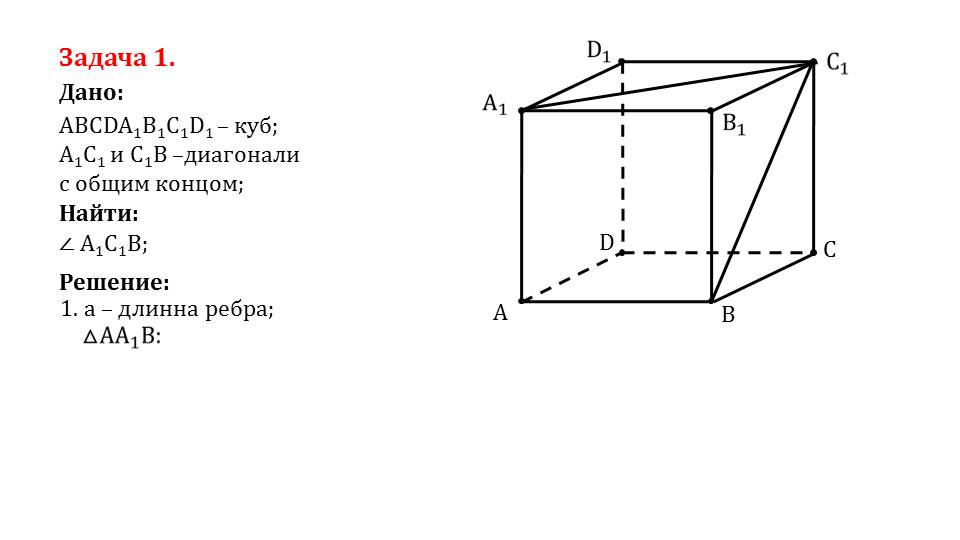
Далее автор предлагает проработать 2 задачи:
- найти угол куба при соответствующих исходных данных;
- доказать, что данная фигура – правильный тетраэдр, найти отношение площади куба к площади тетраэдра, если даны куб и диагонали граней.
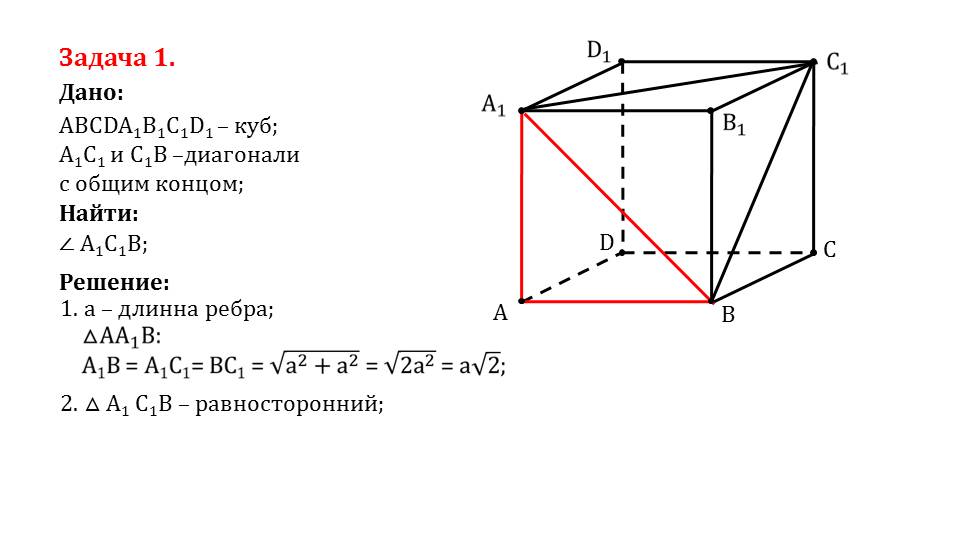
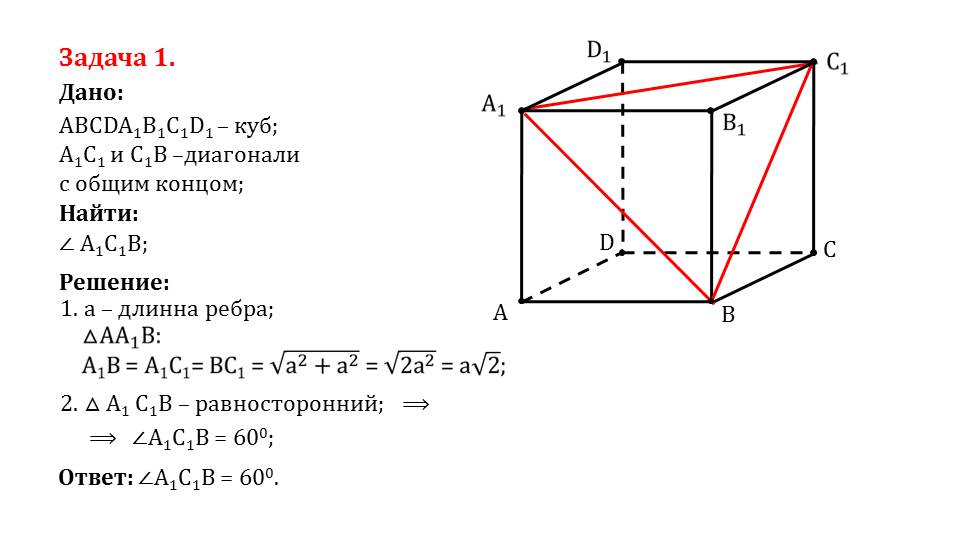
При решении задач строится чертеж фигуры. В ходе решения, при необходимости, чертеж может быть дополнен различными элементами. В задачах повторяется пройденный материал, так как при решении используются изученные свойства многогранников.
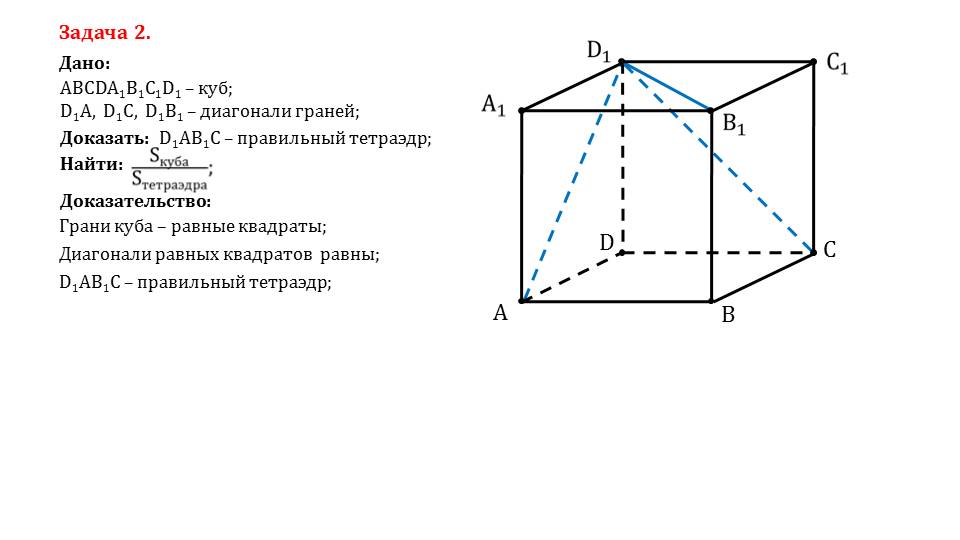
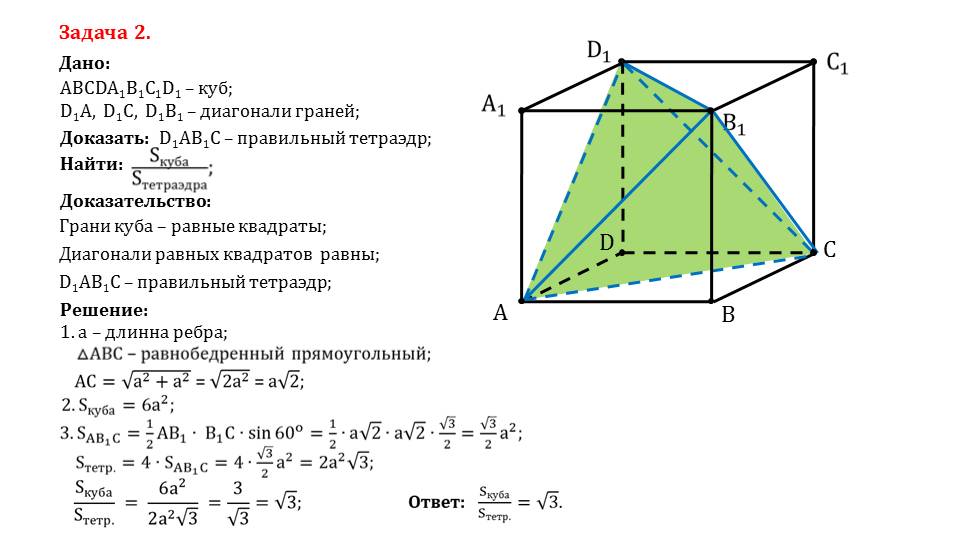
Учитель может применить данную презентацию при подготовке как к теоретической части урока, так и практической. Все описания сопровождаются рисунками, а задачи детально разобраны, что позволит ученикам изучить данный материал самостоятельно без чьей-либо помощи.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 3821 |
| Номер материала | 905 |