
Презентация "Многогранный угол"

Краткое описание документа:
Презентация «Многогранный угол» - это наглядный материал для представления ученикам учебной информации по теме. В ходе презентации представляются теоретические основы понятия многогранного угла, доказываются основные свойства многогранного угла, которые необходимо знать для решения задач. С помощью пособия учителю легче сформировать представление о многогранном угле, умение решать задачи по теме. Презентация в числе других наглядных средств способствует повышению эффективности урока.
В презентации применяются приемы, способствующие улучшению подачи учебного материала. Это анимационные эффекты, выделение цветом, вставка рисунков, схем. Применяя анимационные эффекты, информация подается последовательно, выделяя важные моменты. С помощью анимации построения представляются более живыми, близкими к традиционной демонстрации с помощью классной доски, чтобы ученики легче понимали представляемые свойства. Использование средств выделения помогает ученикам легче запомнить учебную информацию.
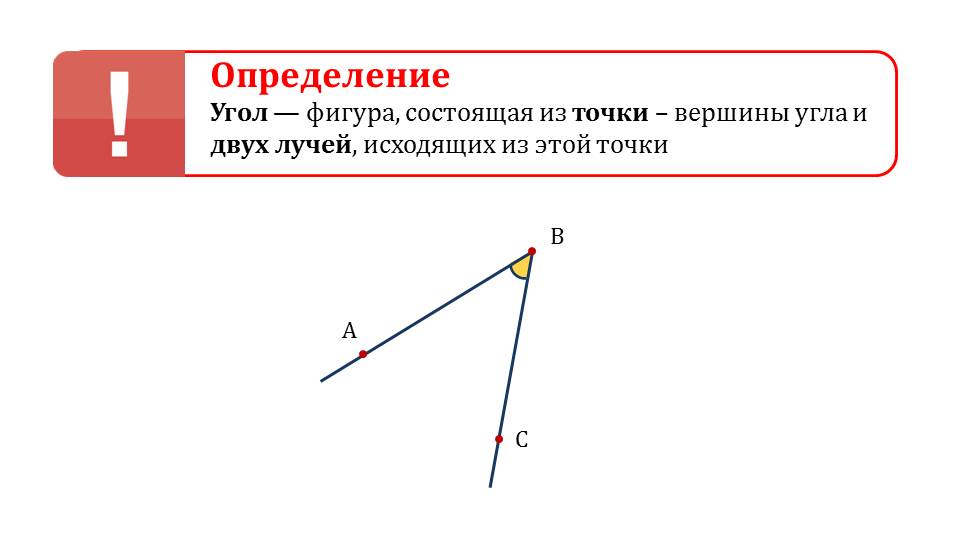
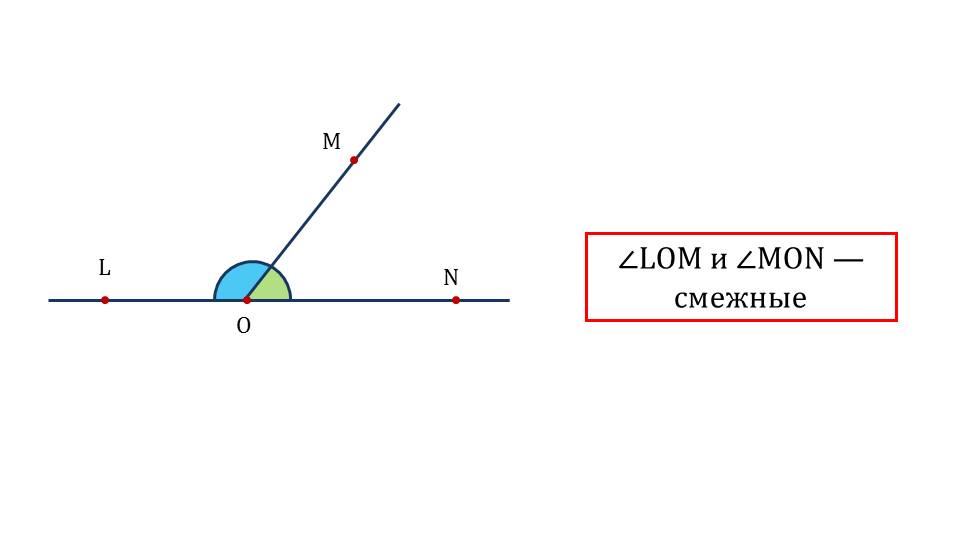
Демонстрация начинается с напоминания учебного материала, с которого начиналось в курсе математики изучение углов. Определение угла как фигуры, состоящей из точки и двух лучей, что исходят из точки. Под определением дано изображение угла ∠АВС, обозначен угол, вершина и точки на лучах. Далее напоминается информация о том, что такое смежные углы ∠LOM и ∠MON. На рисунке изображены смежные углы, обозначены сами углы, вершина О и точки на лучах – L, M, N. Моделью угла служит циркуль, изображенный на слайде 4. Раствор циркуля может меняться, создавая углы различной величины.

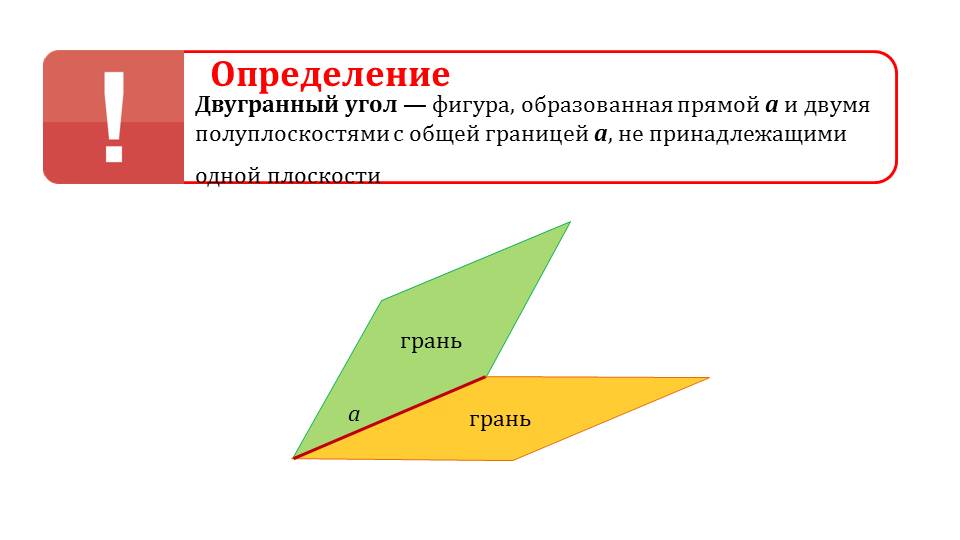
С помощью слайда 5 ученикам напоминается определение двугранного угла как фигуры, составленной из двух полуплоскостей, не принадлежащих одной плоскости, и их общей границей – прямой. Под текстом определения изображен двугранный угол. Примерами многогранных углов служат крыши домов. На рисунке слайда 6 изображены здания с двугранной и многогранной крышей.
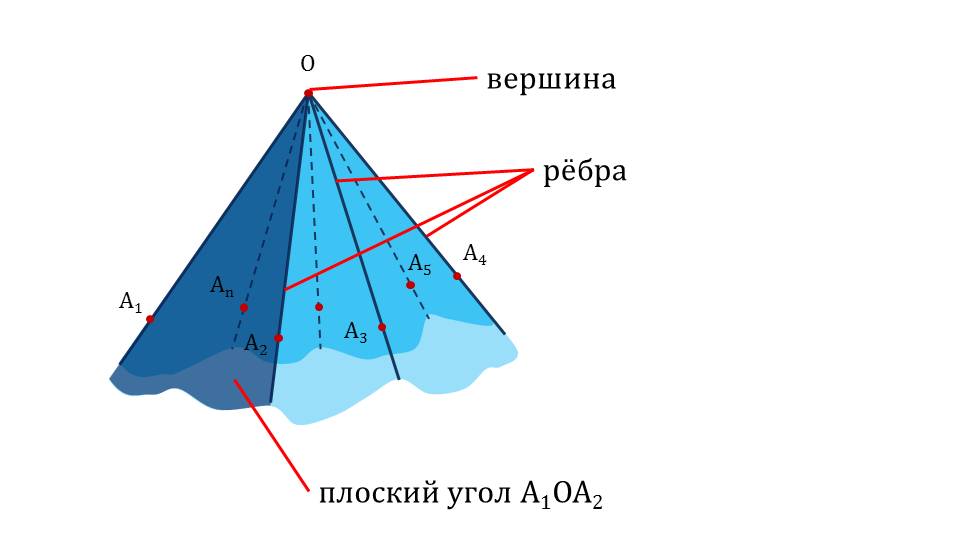
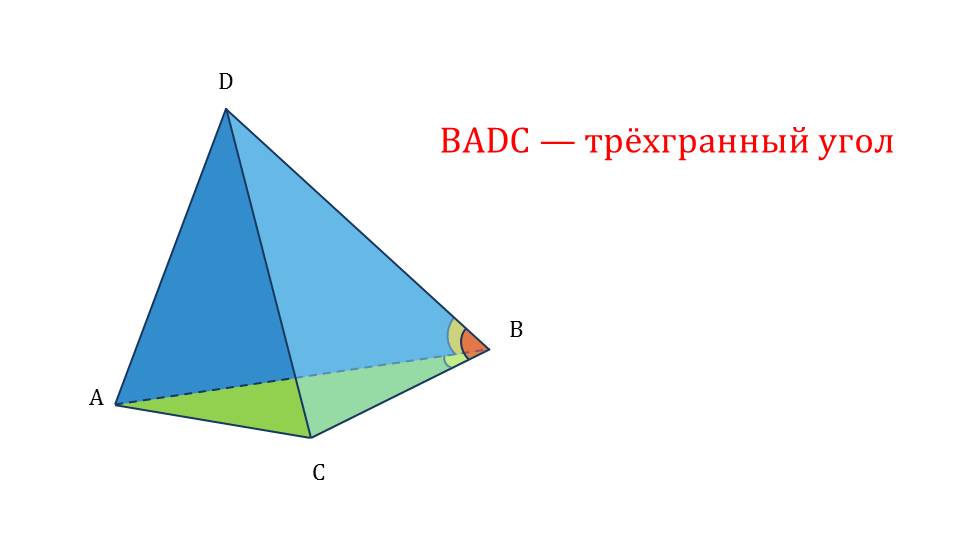
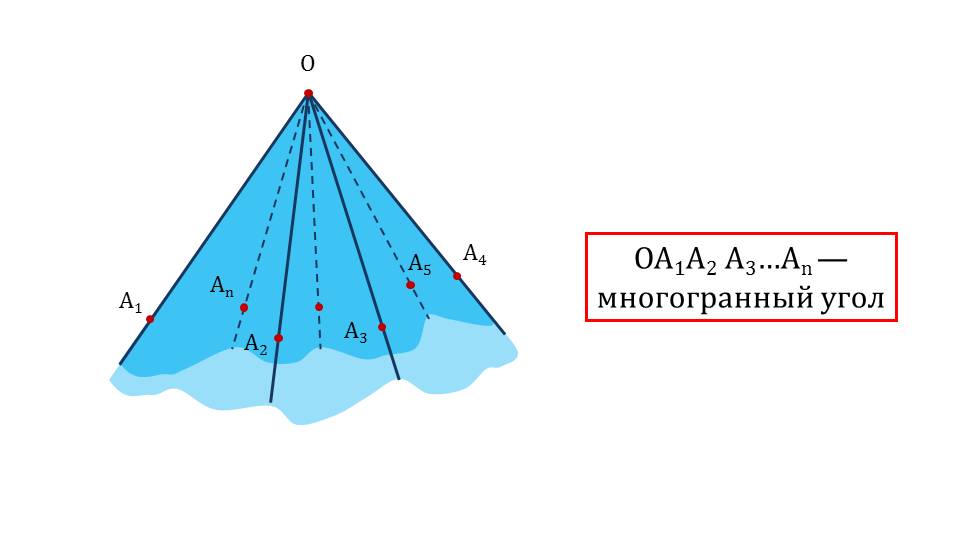
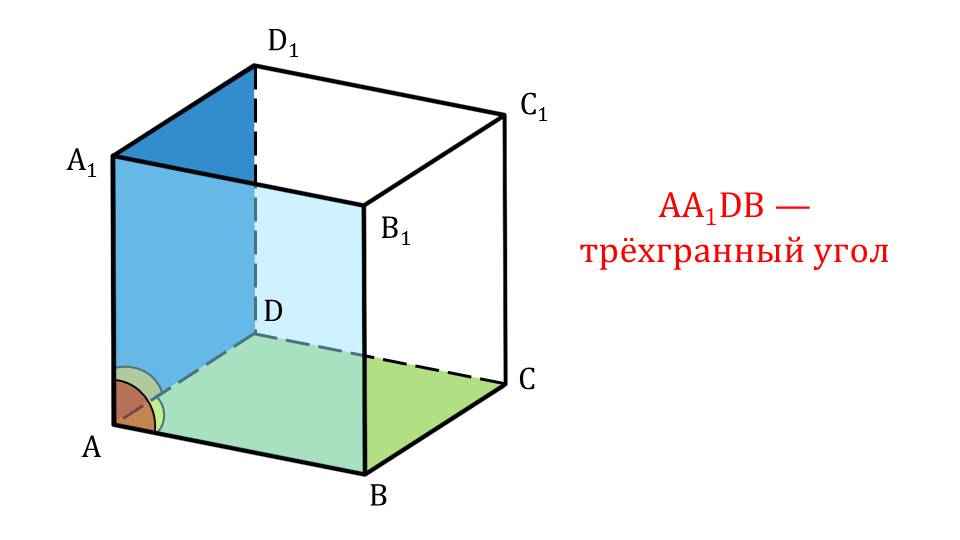
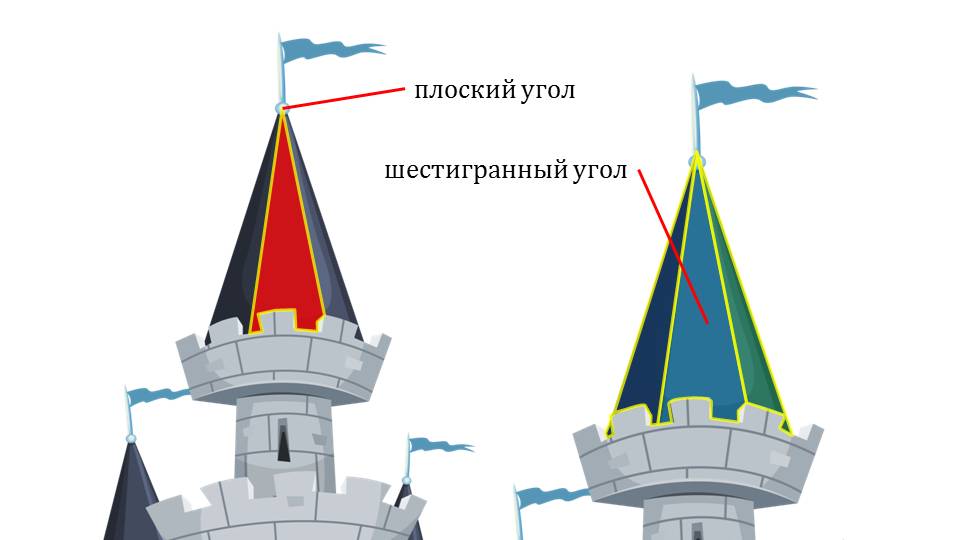
На слайде 7 демонстрируется изображение многогранного угла ОА1А2А3…Аn. На рисунке обозначена вершина угла, на каждом луче отмечена точка, создавая обозначение многогранного угла по вершине и лучам. Обозначение выведено рядом с рисунком и заключено в рамку для запоминания. Рассматривается строение многогранного угла ОА1А2А3…Аn.. На его изображении отмечена вершина О, ребра ОА1,…, ОАn, плоский угол А1ОА2. Далее демонстрируется трехгранный угол ABCD, в котором отмечены плоские углы. Трехгранный угол AA1DB представлен в кубе ABCDA1B1C1D1, изображенном на рисунке слайда 10. На изображении выделен трехгранный угол, формирующие грани которого окрашены в различные цвета, и обозначены плоские углы. Следующий слайд демонстрирует крыши зданий, у которых форма – шестигранный угол. На рисунке отмечен плоский угол и шестигранный угол.
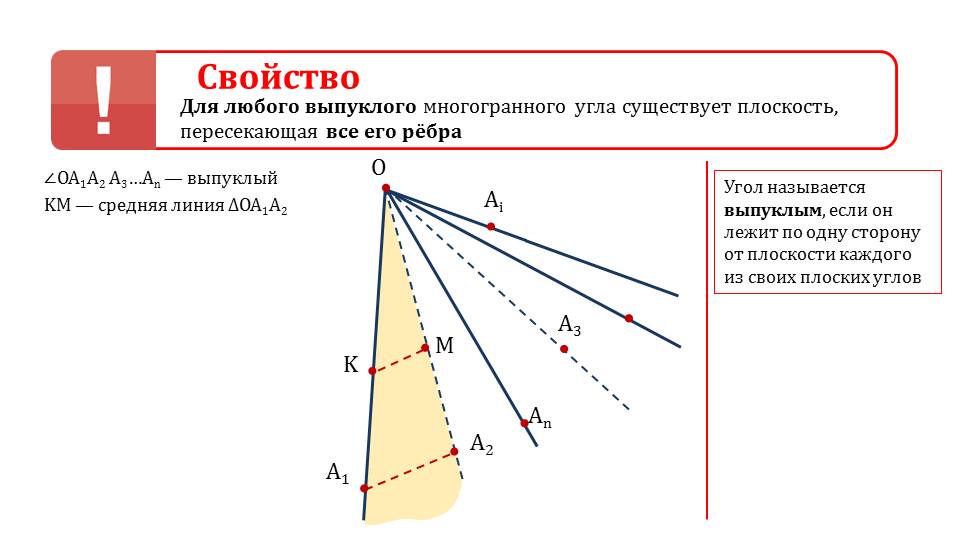
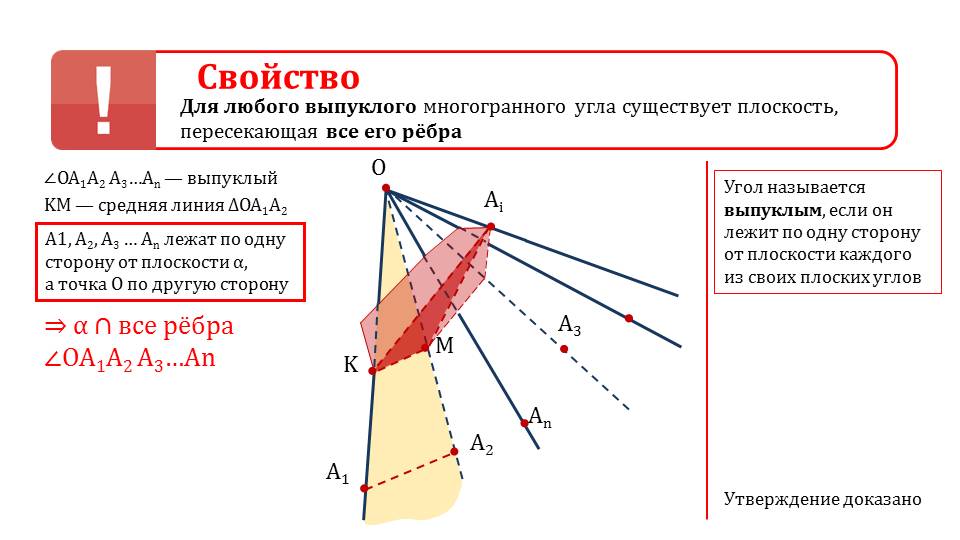
Представлено свойство о существовании плоскости, пересекающей все ребра выпуклого многогранного угла. Чтобы понимать суть свойства, необходимо знать определение выпуклого угла. Оно отмечено рядом со свойством. В определении указано, что выпуклый угол находится по одну сторону от плоскости, которая содержит каждый из плоских углов. Условием теоремы о свойстве многогранного угла предусмотрено, что имеется выпуклый многогранный угол ∠ ОА1А2А3…Аn. На лучах ОА1 и ОА2 отмечены точки К и М, соединение которых составляет среднюю линию треугольника Δ ОА1А2. Плоскость, проходящая через КМ и некоторую точку Аi, располагается таким образом, что все точки А1, А2, А3, …Аn находятся по одну сторону от α, а вершина угла точка О лежит по другую сторону плоскости. Из этого следует, что плоскость пересекает все ребра выпуклого многогранного угла. Теорема доказана.
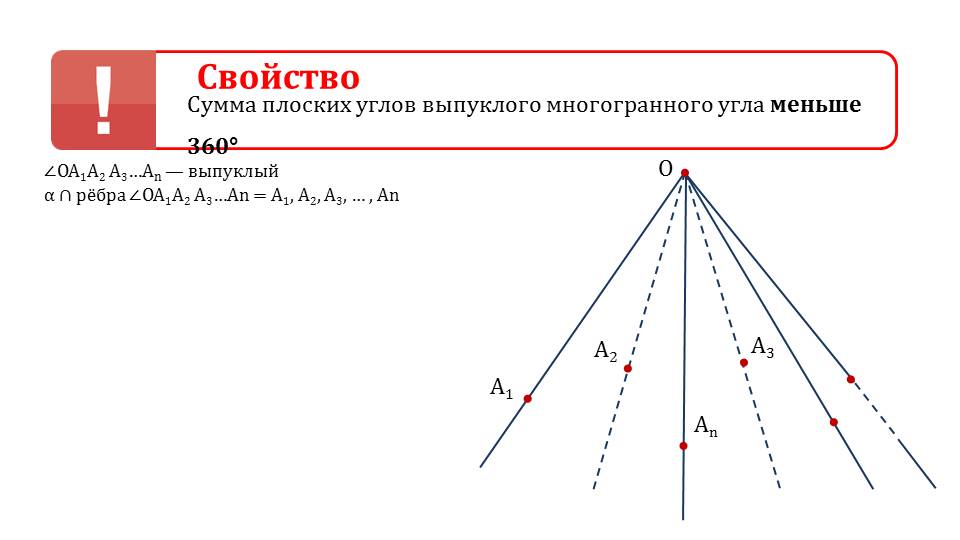
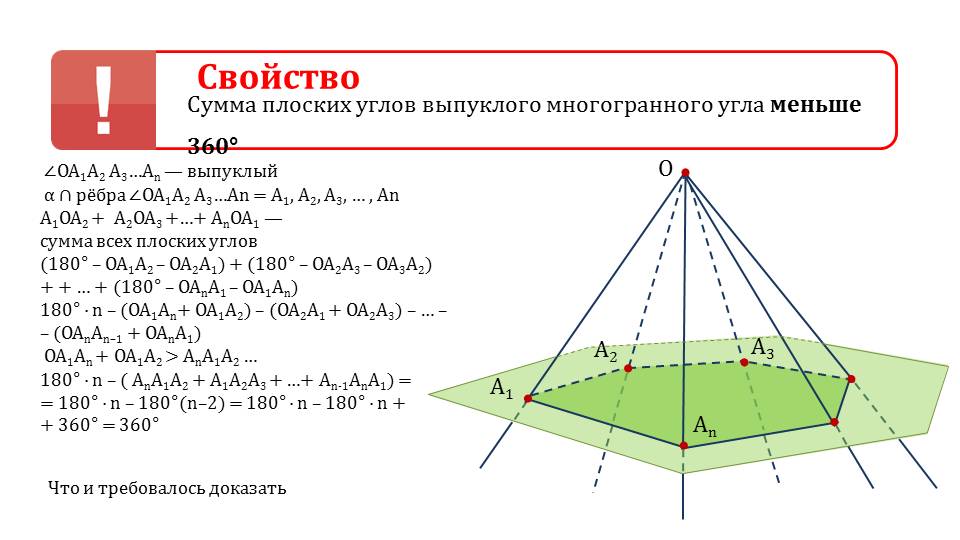
Следующая теорема, представленная на слайде 4, утверждает о том, что сумма всех плоских углов многогранного угла является меньшей 360°. Теорема формулируется в виде свойства, выделенного в красную рамку для запоминания. Доказательство свойства иллюстрируется на рисунке, на котором изображен многогранный угол ∠ ОА1А2А3…Аn. На многогранном угле отмечены вершина О, точки, принадлежащие лучам, А1, А2,А3,…Аn. Это выпуклый многогранный угол. Угол пересекается плоскостью, пересекающей лучи в точках А1, А2,А3,…Аn. Сумма плоских углов многогранного угла представлена выражением А1ОА2+А2ОА3+…+ АnОА1. Зная сумму углов треугольника, каждый из плоских углов представляется выражениями, например, А1ОА2=180°- ОА1А2- ОА2А1 и т.п. В результате преобразования выражения получаем 180°·n-( ОА1Аn+ ОА1А2)-…-( ОАnАn-1+ ОАnА1). Учитывая справедливость неравенства ОА1Аn+ ОА1А2> АnА1А2…, вычисляем 180°·n-( АnА1А2+ А1А2А3+…+ Аn-1АnА1=180°·n-180°(n-2)=360°. Утверждение доказано.
Презентация «Многогранный угол» применяется для повышения эффективности традиционного урока в школе. Также данное наглядное пособие может стать инструментом преподавания в ходе дистанционного обучения. Материал может быть полезен ученикам, самостоятельно осваивающим тему, а также тем, кому требуется дополнительное занятие для более глубокого ее понимания.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 10014 |
| Номер материала | 898 |