
Презентация "Осевая и центральная симметрия"

Краткое описание документа:
В повседневной жизни нам часто встречаются предметы, которые обладают свойством симметрии. Симметрия изучается и в курсе геометрии, причем, даже не один час. На данную тему отводится целая серия уроков. Чтобы хоть немного разбираться в окружающей нас симметрии, нужно обязательно изучать данную тему в школьном курсе. Но нельзя себе представить симметрию без наглядных примеров.
Такие примеры, конечно, можно показывать на реальных предметах, но тогда их нужно отыскать. Но для этого придется потратить свое время. Хорошим вариантом может стать презентация, где можно разместить и примеры, и теоретические моменты. Здесь, опять же, потребуется время на создание презентации. Если нет свободного и лишнего времени на это, то можно воспользоваться данной презентацией, которую автор выполнил специально для учителей, преподающих математику.


слайды 1-2 (Тема презентации "Осевая и центральная симметрия", пример)
В самом начале презентации определяется симметрия относительно прямой. Здесь говорится, о том, что точки называются симметричными относительно некоторой прямой, если эта прямая пересекает середину отрезка, образованного этими точками, под углом 90 градусов. К данному определению здесь же имеется и чертеж, на котором показано, как выглядят точки, симметричные относительно прямой.
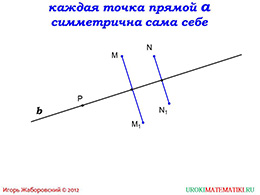

слайды 3-4 (примеры, определение симметричной прямой)
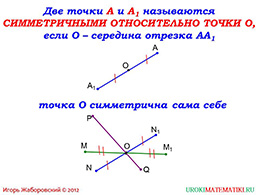
Затем на слайде идет замечание, которое говорит, что любая точка, принадлежащая прямой, является симметричной сама себе. Что показано на чертеже. Также здесь показаны примеры двух других пар симметричных точек, не лежащих на заданной прямой.
Далее в презентации определяется фигура, симметричная относительно заданной прямой. Ее называют симметричной относительно этой прямой, если любая ее точка симметрична другой точке, принадлежащей этой же фигуре относительно этой прямой. Тогда эту прямую называют осью симметрии, а фигура, говорят, обладает свойством осевой симметрии.
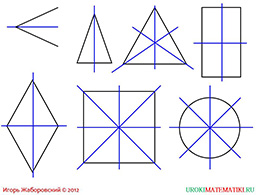
слайды 5-6 (примеры)
На следующем слайде автор привел самые разнообразные примеры фигур с осевой симметрией. Сюда входят угол с проведенной прямой, являющейся биссектрисой, треугольник с равными боковыми сторонами с медианой, высотой или биссектрисой, равносторонний треугольник, имеющий одновременно 3 оси симметрии, у прямоугольника и ромба имеется по паре осей симметрии, а также квадрат с тремя осями симметрии и круг, у которого бесконечно много таких осей.

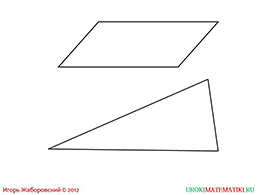
слайды 7-8 (примеры)
На следующем слайде автор показывает два примера, где фигуры не имеют осей симметрии, то есть такие фигуры, которые не обладают симметрией. К таковым относятся произвольный треугольник и параллелограмм. На самом деле, таких примеров очень много, но автор подобрал для демонстрации самые популярные, которые чаще других можно встретить в курсе геометрии.

слайды 9-10 (примеры)
Но в теме была заявлена еще и центральная симметрия. Поэтому автор далее в презентации поместил определение понятия симметрии относительно точки. Здесь автор определяет фигуру, симметричной относительно некоторой точки O, как такую, для которой каждая ее точка симметрична некоторой точке этой же фигуры относительно заданной точки О. Здесь же говорится, что эта точка O является центром симметрии, а, значит, фигура обладает в этом случае центральной симметрией.
Далее в презентации приводятся примеры фигур c центральной симметрией и без нее. С центральной симметрией здесь имеются разных фигур. К фигурам без центральной симметрии относится произвольный треугольник.

слайд 11 (примеры)
Как уже было сказано выше, в повседневной жизни каждый встречал хотя бы раз предмет, обладающий любым из видов симметрии. Это могли быть растения, цветы, животные, насекомые. Довольно часто симметричные элементы можно встретить в архитектурных сооружениях. Именно такие примеры с изображением симметричных объектов представлены в презентации.
Данная презентация будет полезна как учителю, так и обучающимся. Ведь здесь представлена только важная информация, которая в дальнейшей жизни обязательно пригодится, хотя бы даже на уроках геометрии.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 10454 |
| Номер материала | 327 |