
Урок "Прямоугольник"

Краткое описание документа:
В данном видеоуроке автор представил на рассмотрение тему по геометрии для изучения в 8-м классе о прямоугольнике, его свойствах и особенностях. Перед тем, как приступить к ознакомлению с уроком, автор рекомендует учащимся вспомнить определение и свойства параллелограмма самостоятельно. При необходимости можно вернуться на несколько уроков назад. После повторения освоение новой темы «Прямоугольник» не вызовет трудностей у школьников.

Итак, рассмотрим понятие прямоугольника и его особенности.
Вначале автор акцентирует внимание учащихся на определении прямоугольника. Прямоугольник – это выпуклый многоугольник, который является параллелограммом с прямыми углами.

Прямоугольник характеризуется всеми свойствами параллелограмма, так как является его частным случаем.
Свойства прямоугольника (как параллелограмма):
– стороны, лежащие напротив друг друга, равны;
– точка пересечения диагоналей фигуры делит диагонали на равные отрезки.
Но помимо свойств прямоугольника таких же, как у параллелограмма, прямоугольник характеризуется еще другими особенностями. Рассмотрим эти положения более подробно: свойство прямоугольника и признак.
Свойство прямоугольника: диагонали прямоугольника являются равными отрезками. Посмотрим на рисунок: на нем изображен прямоугольник ABCD с диагоналями AC и DB. Рассмотрим прямоугольные треугольники ADC и DAB: они имеют общую сторону (общий катет) AD, а стороны AB и CD (катеты)равны между собой. Треугольники ADC и DABравны, так как у них выполняется равенство двух катетов. Из равенства треугольников следует равенство гипотенуз AC = BD, которые являются диагоналями прямоугольника. Мы доказали утверждение – первое свойство прямоугольника.
Теперь перейдем к обратному утверждению, которое известно как признак прямоугольника.
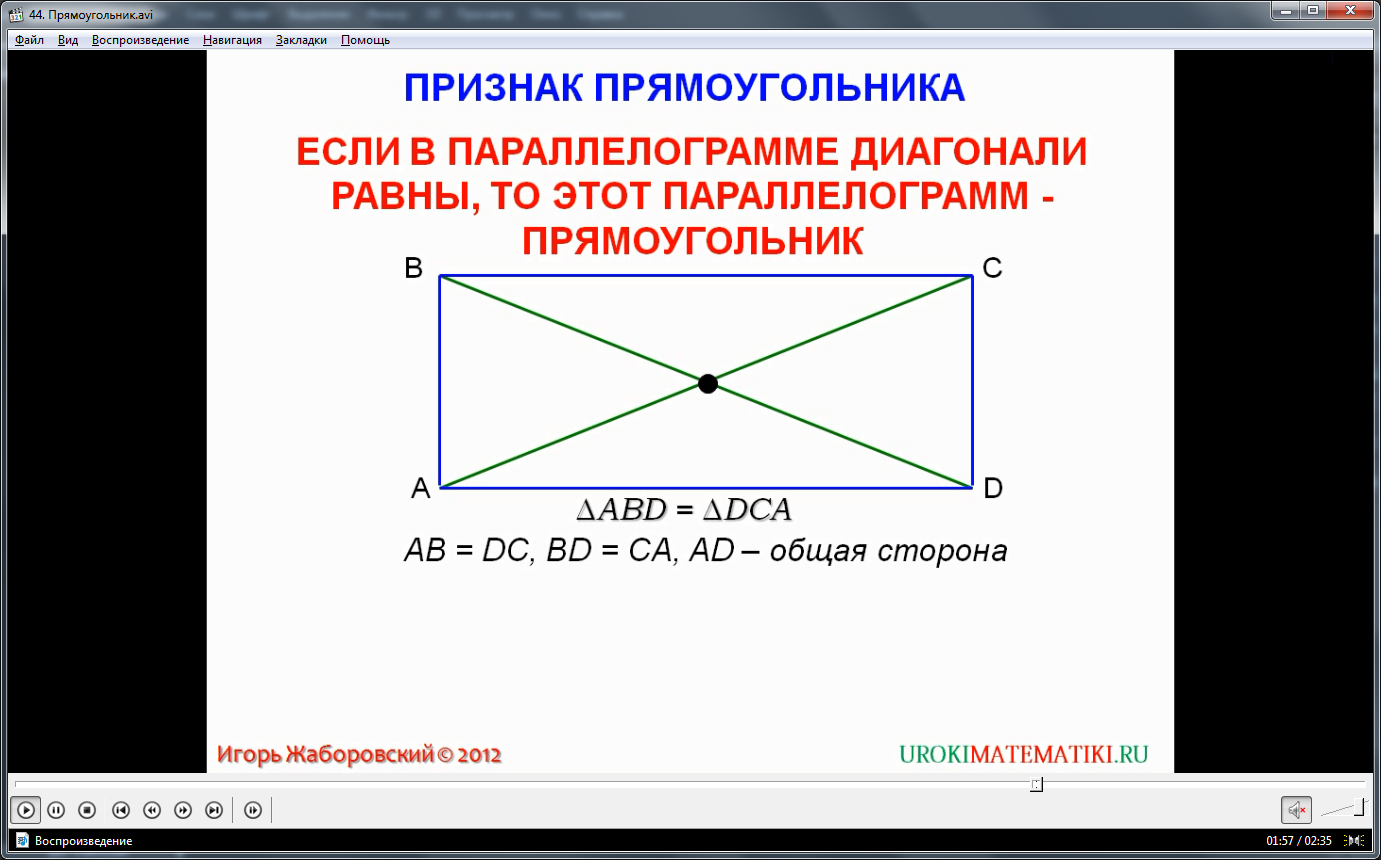
Признак прямоугольника: если в параллелограмме равны диагонали, то этот параллелограмм является прямоугольником. На рисунке показан параллелограмм ABCD, у которого равны диагонали AC и BD. Рассмотрим треугольники ADB и ACD: сторона AB равна стороне CD, сторона DB равна CA как противоположные стороны параллелограмма; AD – общая сторона рассматриваемых треугольников. Сделаем вывод, что треугольники ADB и ACDравны, так как у них выполняется равенство трех сторон. Из равенства треугольников следует равенство углов A и D. Мы знаем, что в параллелограмме противоположные углы равны. Значит, угол A равен углу C, а угол B равен углу D. Т.е. углы A, B, C и D равны между собой. Параллелограмм – это выпуклый четырехугольник, сумма всех углов в нем равна 360 градусов. Найдем величину каждого угла 360 / 4 = 90 градусов. Параллелограмм с углами 90 градусов является прямоугольником. Признак прямоугольника доказан.
Данная видеопрезентация может быть с легкостью применена учителем при проведении урока геометрии, т.к. описывает все важные теоретические аспекты темы, наглядно представляет изучаемый материал. Информация изложена последовательно и доступно, поэтому ученики могут изучить урок по видеоматериалам, не прибегая к чьей-либо помощи.
Если тема «Прямоугольник» внимательно проработана учениками, то изученные положения (свойства и признака прямоугольника) будут легко и без затруднений применяться на практике при дальнейшем обучении.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 4948 |
| Номер материала | 582 |