
Урок "Трапеция"

Краткое описание документа:
Этот видео урок посвящается трапеции. На первом изображении показан четырехугольник DCBA. Этот выпуклый четырехугольник имеет две параллельные противоположные стороны. Две другие, тоже противоположные, стороны не являются параллельными. Такая геометрическая фигура называется трапецией. Как опять же показано в видеоматериале, элементы трапеции имеют свои особые названия. Параллельные стороны трапеции называются ее основаниями. Так, на чертеже, верхняя сторона CB является основанием трапеции или верхним основанием.
Сторона DA, параллельная стороне CB, также является основанием или нижним основанием трапеции. Сторона же DC, и сторона BA не являются параллельными. Эти два элемента трапеции называются ее боковыми сторонами. Таким образом, трапеция имеет две боковые стороны и два основания. Если середины боковых сторон соединить прямой линией, то получится отрезок, который называется средней линией трапеции. Средняя линия трапеции обладает таким свойством: она параллельна основаниям и по длине равна полусумме их длин. В дальнейшем эта теорема может быть использована для решения задач на нахождение элементов трапеции. Слово «трапеция» пришло к нам из греческого языка. В переводе это слово обозначает «стол», «еда» (сравнить - трапеза). Такое же название и у гимнастического снаряда. Действительно, чертежи трапеций чем-то напоминают эти предметы.
В зависимости от соотношения и расположения боковых сторон, различают некоторые частные случаи трапеции. На следующем изображении видео урока показана трапеция с равными боковыми сторонами. Такая трапеция называется равнобедренной или равнобокой. Равнобедренная трапеция имеет свои особенные свойства. Во-первых, углы при основании равнобедренной трапеции равны. Во-вторых, диагонали равнобедренной трапеции тоже равны. Эти свойства необходимо запомнить и применять при решении задач.

Еще один частный случай трапеции показан на третьем изображении видео урока. Такая геометрическая фигура называется прямоугольной трапецией. Здесь особенностью является то, что одна из ее боковых сторон перпендикулярна обоим основаниям. Эта боковая сторона является высотой трапеции. Нетрудно заметить, что если вторую боковую сторону тоже провести перпендикулярно основаниям, то прямоугольная трапеция превратится в прямоугольник.
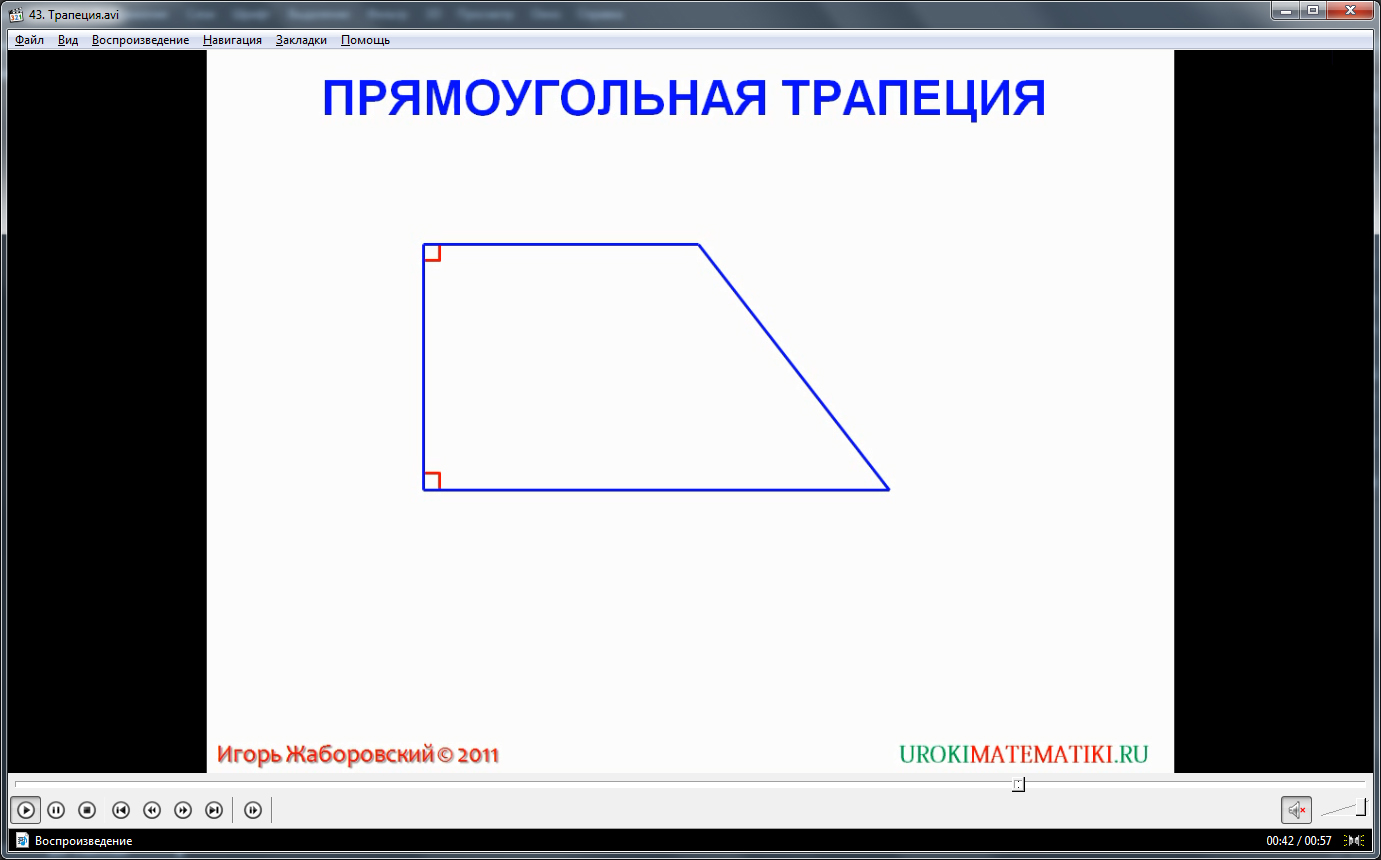
Напоследок вернемся к первому изображению данного видеоматериала и мысленно выполним для трапеции DCBA дополнительные построения. Проведем из вершин C и B на основание DA два перпендикуляра. Наша трапеция разобьется на два треугольника и прямоугольник. Если из вершины B параллельно боковой линии CD провести отрезок прямой до пересечения с основанием DA, получим треугольник и параллелограмм. Подобные построения часто оказываются просто необходимыми при решении задач на определение элементов трапеции.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 4285 |
| Номер материала | 581 |