
Урок "Ромб и квадрат"

Краткое описание документа:
Перейдем к рассмотрению следующей темы по геометрии с помощью представленного видеоурока. В уроке учащиеся изучат такие геометрические фигуры, как ромб и квадрат, ознакомятся с их свойствами.
Чтобы освоение новой темы проходило легко, рекомендуем школьникам вспомнить определения и свойства параллелограмма и прямоугольника, изученные в предыдущих темах. Учащиеся могут самостоятельно повторить пройденный материал, используя видеоуроки на нашем сайте.
Начнем изучение новой темы с такого многоугольника, как ромб.
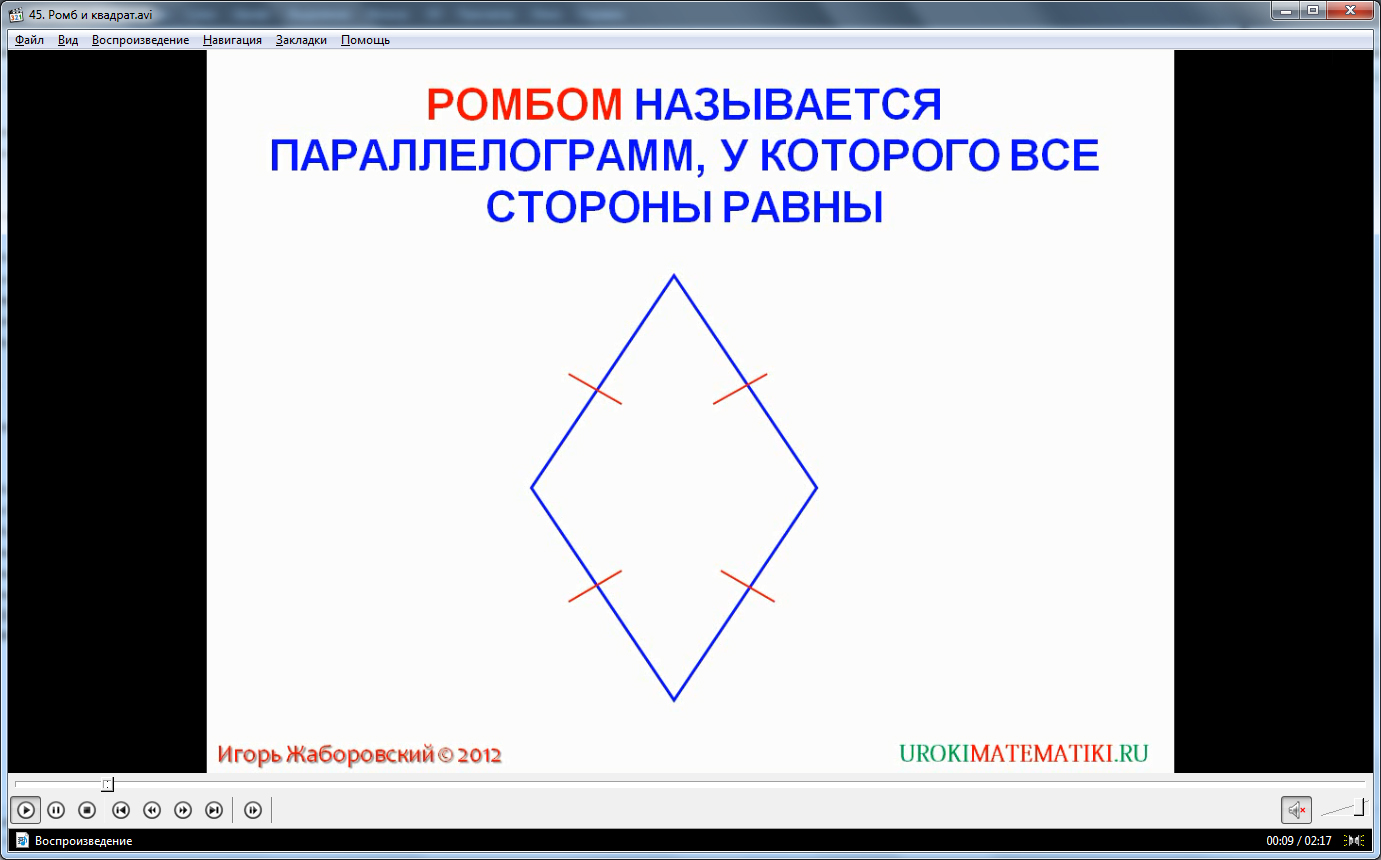
Ромб – это многоугольник, представляющий собой параллелограмм, у которого все стороны равны между собой. Изображенный ромб мы можем увидеть на рисунке. Ромб – это параллелограмм, ему присущи все свойства, которыми характеризуется параллелограмм: равенство сторон, лежащих напротив друг друга, и равенство отрезков, которые делятся точкой пересечения диагоналей на равные отрезки.
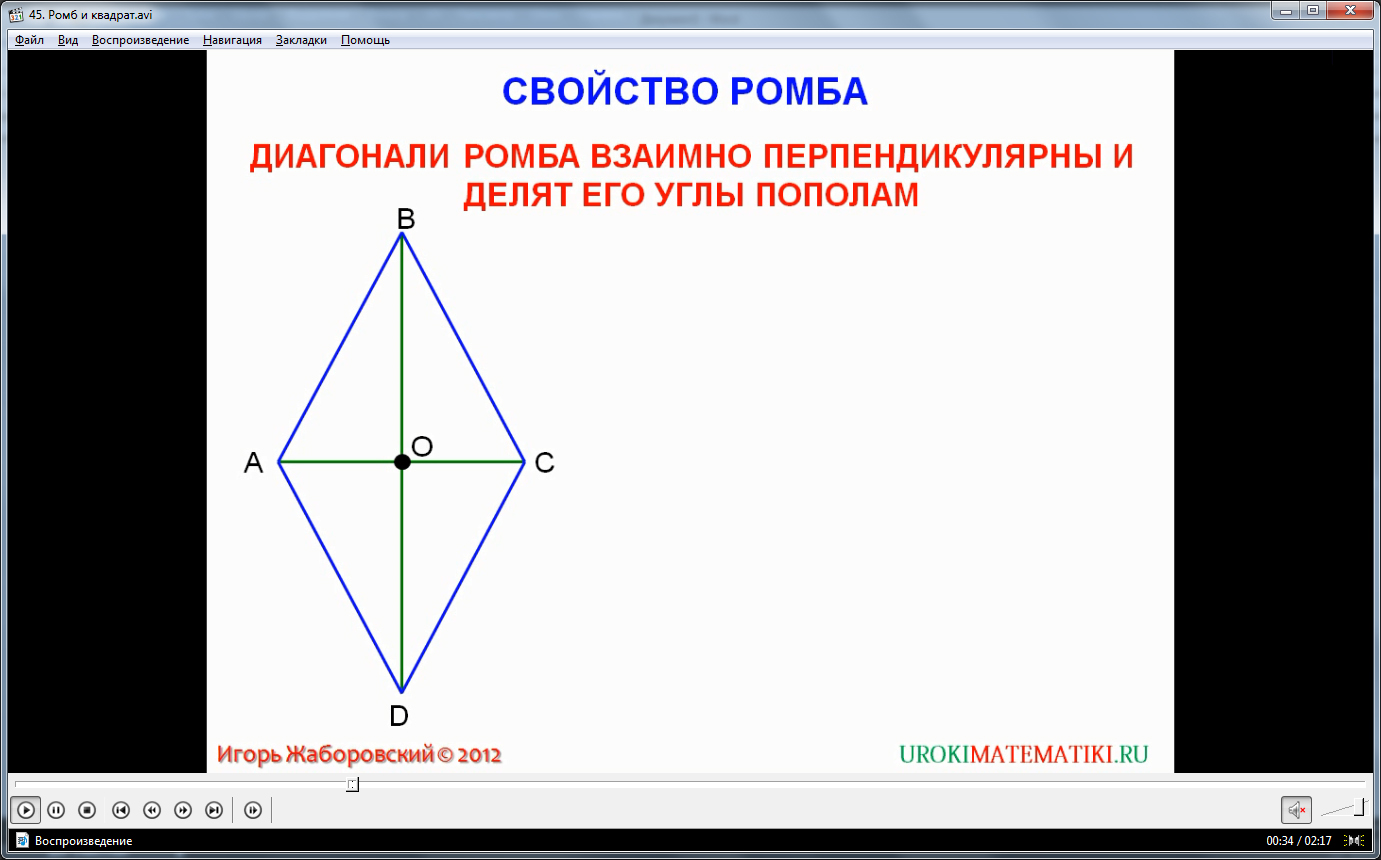
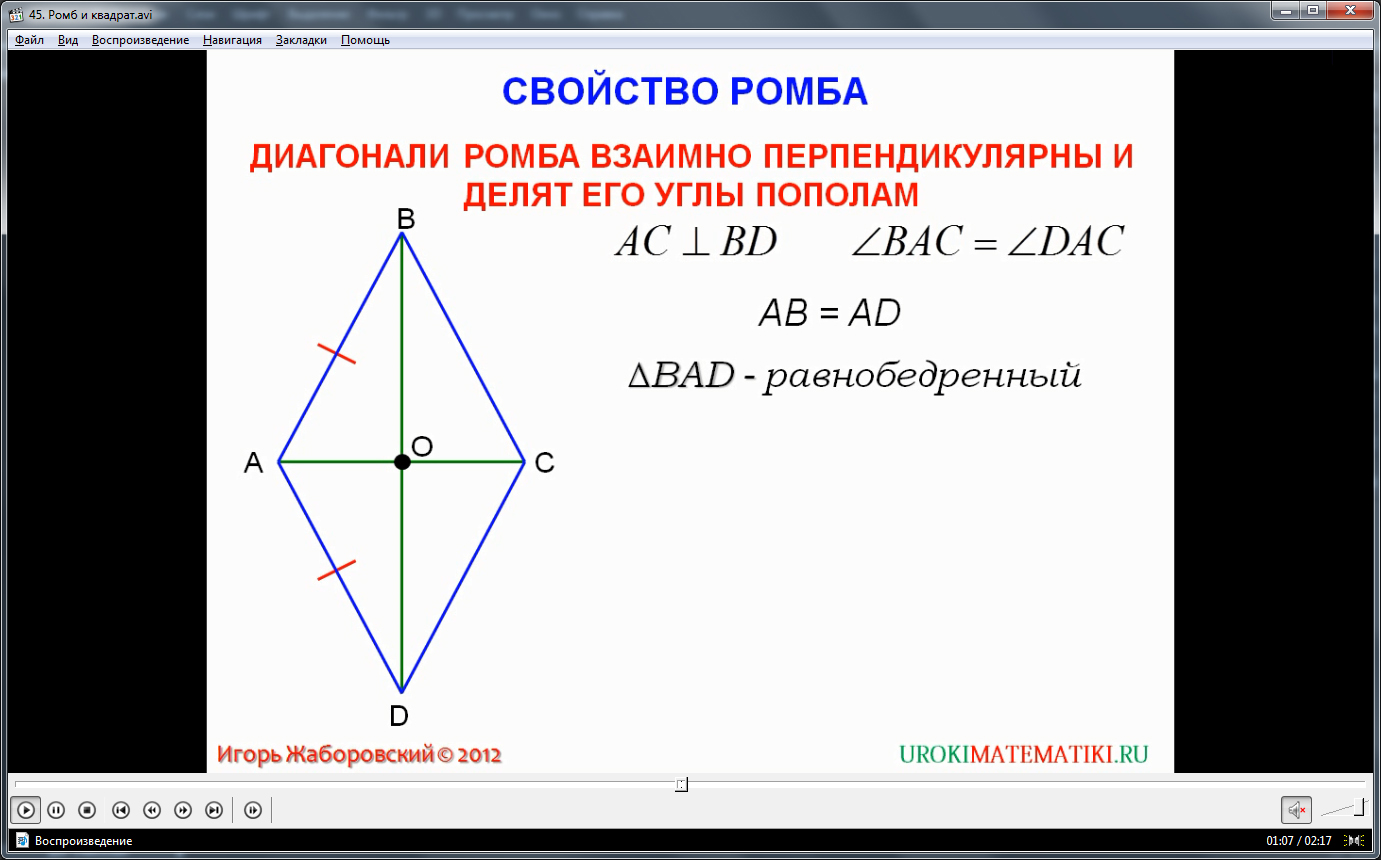
Рассмотрим еще одно свойство ромба: перпендикулярность диагоналей ромба относительно друг друга и деление углов ромба диагоналями на равные углы. Свойство необходимо доказать. Начертим ромб ABCD. Диагонали ромба AC и DB, пересечение их – точка О. Нужно доказать, что отрезок CA перпендикулярен DB, и каждаяиз диагоналей делит углы ромба пополам. Для начала докажем, что угол CAB равен углу CAD. Рассмотрим треугольник ABD. Из определения мы знаем, что у ромба равные стороны BA = DA. Значит, треугольник ABD – равнобедренный. Используя свойство ромба, утверждающее, что отрезки диагоналей, на которые делит их точка пересечения, равны, запишем, что отрезок BO равен отрезку OD.Обозначим равенство сторон BA и DA, отрезков BO и OD на рисунке. Мы пришли к выводу: AO – это медиана треугольника ABD. Зная, что рассматриваемый треугольник ABD равнобедренный, то AOявляется также биссектрисой и высотой данного треугольника. Так как AO – высота, то отрезок CA перпендикулярен DB, что означает перпендикулярность диагоналей ромба относительно друг друга. Так как AO – биссектриса, то угол ромба BAD делится отрезком AO на два равных угла: CAB и CAD. Свойство доказано.
Перейдем к рассмотрению квадрата. Квадрат – это многоугольник, который является прямоугольником с равными сторонами. Прямоугольник – это параллелограмм, значит, квадрат – это параллелограмм с равными сторонами. А мы уже знаем, что параллелограмм, у которого стороны равны, является ромбом. Следовательно, что свойства прямоугольника и ромба можно применить также к квадрату. Выделим основные свойства, которыми обладает квадрат.
Первое свойство: в квадрате все углы равны между собой и равны 90 градусов, что схематично изображено на рисунке.
Второе свойство касается диагоналей:
– диагонали квадрата – это равные отрезки;
– диагонали перпендикулярны относительно друг друга;
– точка пересечения диагоналей делит их на равные отрезки;
– диагонали делят углы квадрата на равные между собой углы.
Обозначение этих положений мы также видим на рисунке.

Итак, в данной теме мы рассмотрели понятия и особенности ромба и квадрата. Применение данных видеоматериалов на уроке геометрии поможет учителю сделать изучение темы наглядным и легко запоминающимся, а также сократит время на подготовку урока.
Изучение теоретических положений будут основой при решении практических задач в дальнейшем. Поэтому важно, чтобы учащиеся усвоили все определения, свойства, особенности фигур. Самостоятельное изучение видеоурока также не вызовет трудностей у школьников.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 5297 |
| Номер материала | 583 |