
Урок "Признаки параллелограмма"

Краткое описание документа:
Как известно, если взять четыре точки (вершины) и последовательно соединить их отрезками прямых, то получится фигура, которая называется четырехугольником. Нужно только, чтобы выбранные вершины не лежали на одной прямой. Если при этом четырехугольник расположится по одну сторону от прямой, проведенной через любую его сторону, то его называют выпуклым. Так можно получить какое-угодно количество четырехугольников. Разумеется, не каждый из них можно назвать параллелограммом.
В этом видео уроке пойдет речь о том, какие из выпуклых четырехугольников являются параллелограммами. Иначе говоря, данный видеоматериал посвящен признакам параллелограмма.
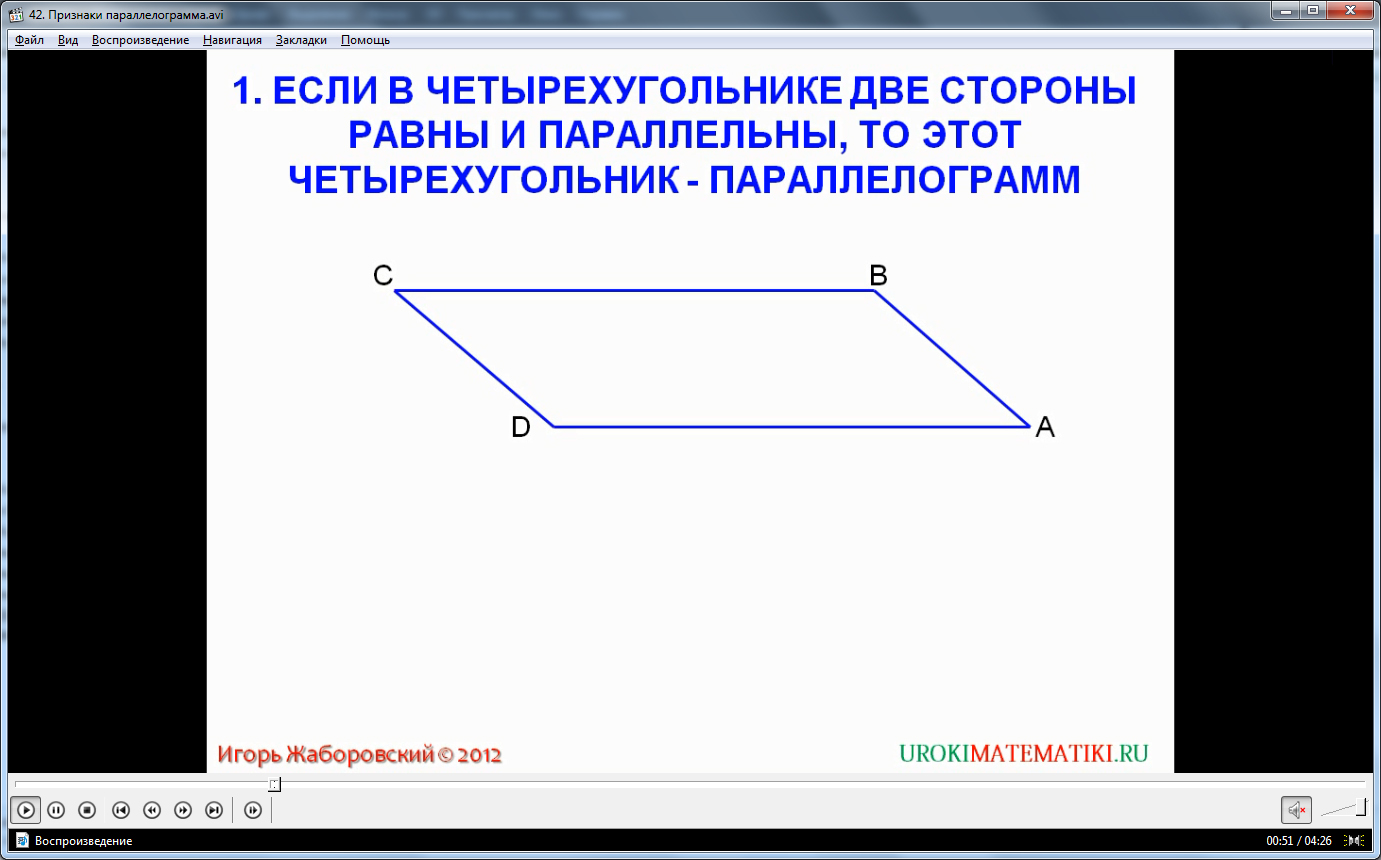
Признак первый заключается в том, что: если в некотором четырехугольнике две стороны равны и параллельны, то этот четырехугольник является параллелограммом. Доказать данное утверждение можно с помощью чертежа, выполненного на слайде видео урока. Действительно, если в четырехугольнике провести диагональ, то получим два равных треугольника. Такой вывод можно сделать на основании одного из признаков равенства треугольников. Треугольники по условию имеют две равные и параллельные друг другу стороны. Дополнительно проведенная диагональ, является общей для обоих треугольников стороной. Углы 1 и 2 на чертеже равны, как внутренние накрест лежащие углы. Из равенства треугольников получается, что углы 3 и 4 также равны. Значит, вторые две стороны будут параллельны друг другу, а наш четырехугольник является параллелограммом.

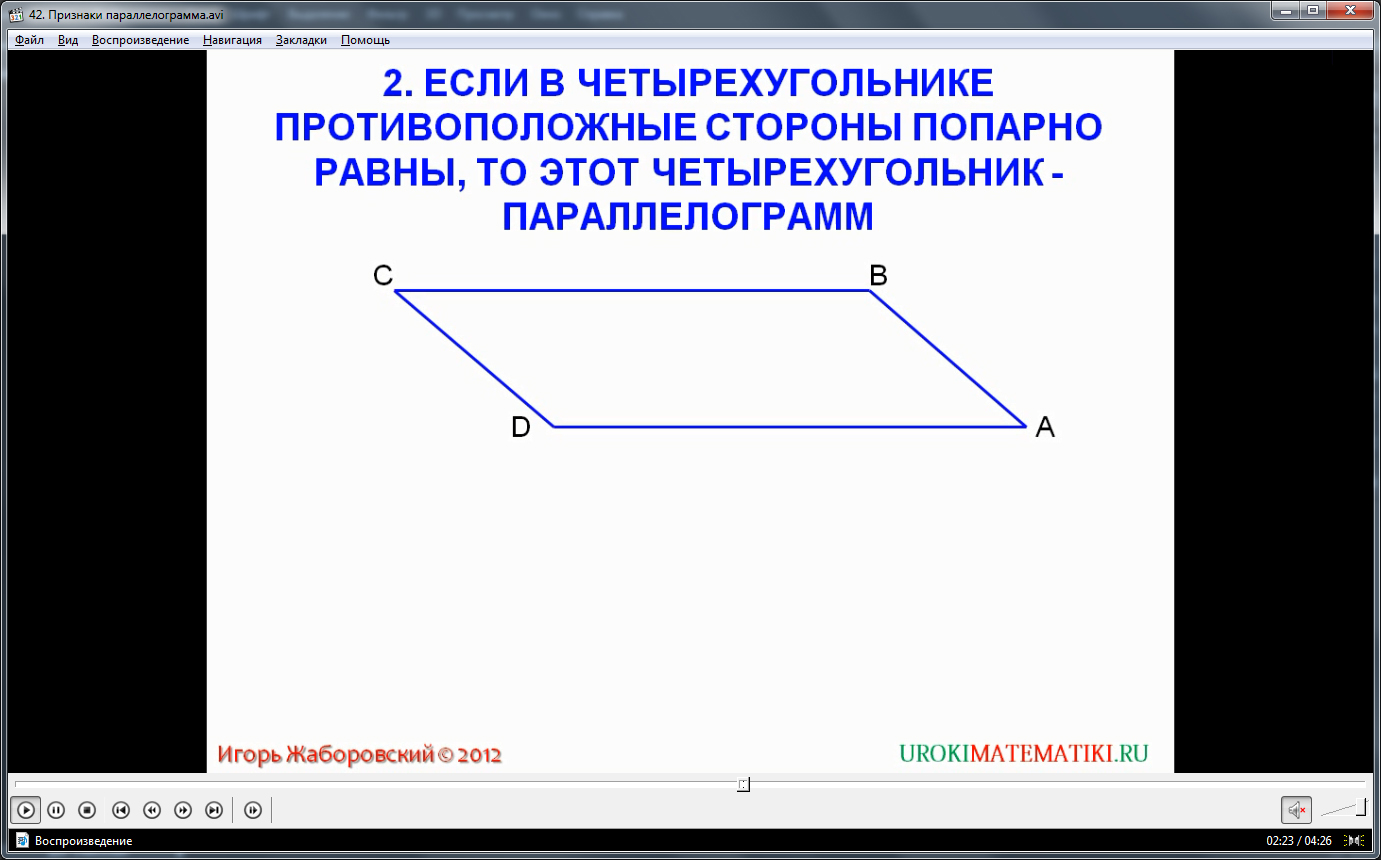
Второй признак утверждает, что данный четырехугольник является параллелограммом, если его противоположные стороны попарно равны. Доказательство этого признака иллюстрирует чертеж следующего слайда видео урока. На чертеже изображен четырехугольник. Как и в предыдущем случае, в нем проведена диагональ, которая делит фигуру на два треугольника и является общей стороной для этих треугольников. Таким образом, треугольники равны по трем сторонам. Действительно, две стороны попарно равны по условию, а третья сторона общая. Но в равных треугольниках против равных сторон лежат равные углы. Следовательно, углы, обозначенные на чертеже как углы 1 и 2, равны, поскольку являются внутренними накрест лежащими. Значит равные по условию стороны, обозначенные как DC и BA, будут параллельными. Аналогичные рассуждения можно привести и относительно двух других сторон CB и DA. Таким образом, утверждение доказано и на чертеже изображен параллелограмм.
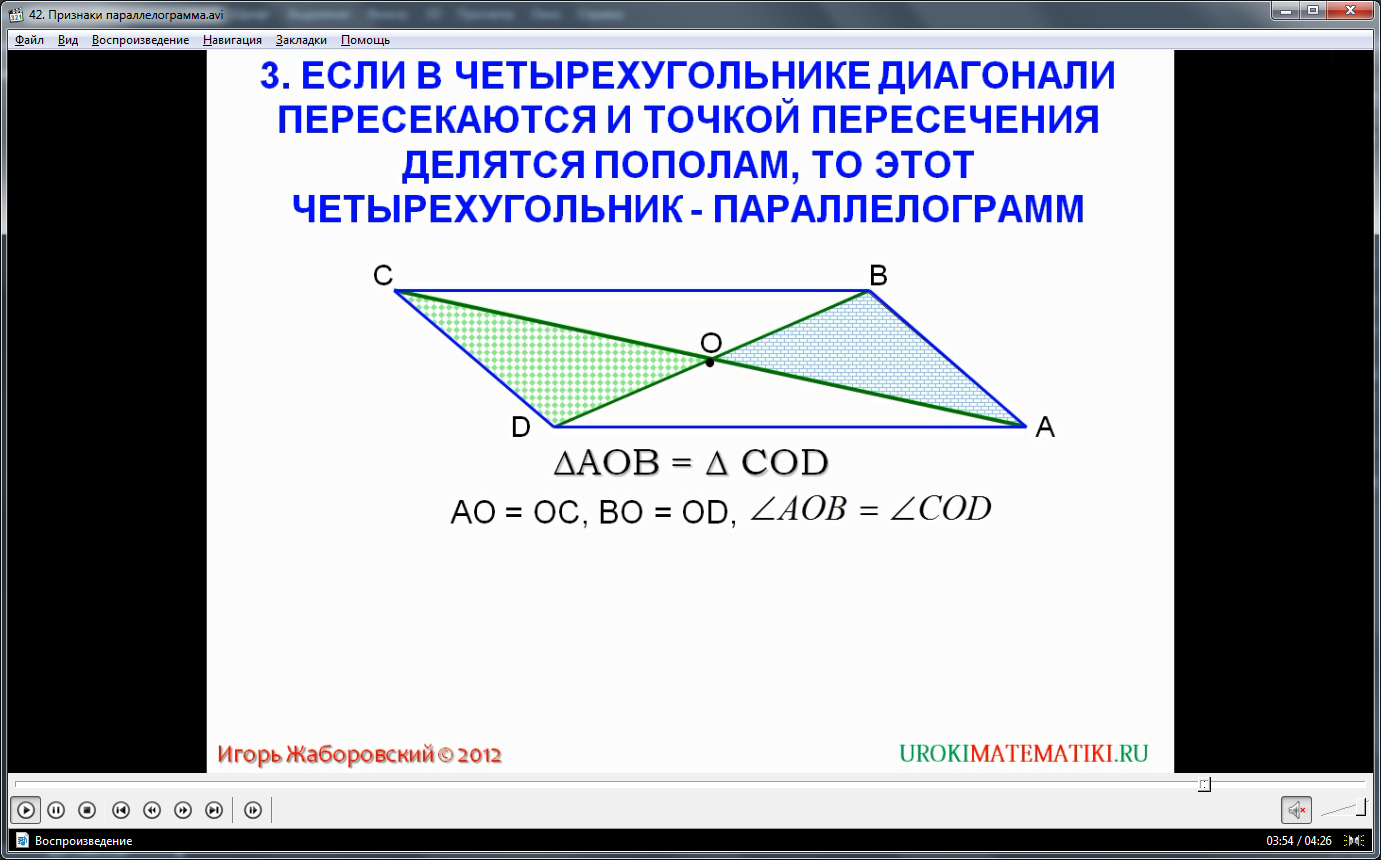
Наконец, третье утверждение состоит в том, что четырехугольник, у которого диагонали в точке пересечения делятся пополам, является параллелограммом. На последнем из слайдов этого видеоматериала опять же изображен четырехугольник. Для доказательства третьего признака параллелограмма, в нем проведены две диагонали. По условию они делятся пополам, то есть отрезок CO равен отрезку OA, а отрезок DO равен отрезку OB. Сами же диагонали, пересекаясь, образуют попарно равные углы. На чертеже угол COD равен углу AOB. Следовательно, заштрихованные треугольники, которые получились в результате пересечения диагоналей, равны по двум сторонам и углу между ними. Стало быть, сторона CD равна стороне AB. Углы, обозначенные на чертеже слайда, данного видео урока, как угол 1 и угол 2, равны. Они лежат в равных треугольниках против равных сторон CD и AB. Поскольку эти углы являются внутренними накрест лежащими, то можно утверждать, что сторона CD параллельна стороне AB.
Итак, в четырехугольнике имеются две равные и взаимно параллельные стороны. Значит, по уже доказанному здесь признаку, показанный на слайде четырехугольник является параллелограммом.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 4595 |
| Номер материала | 580 |