
Презентация "Параллельные плоскости"

Краткое описание документа:
Плоскости в пространстве, как и прямые могут иметь различное взаимное расположение. В предыдущих уроках школьники изучали расположение прямых пространстве, и прямой по отношению к плоскости. Было выяснено, что прямые в пространстве могут быть либо пересекающимися, либо параллельными, либо скрещивающимися.
С помощью данного электронного ресурса можно провести интересный и наглядный урок, который касается расположению плоскостей в пространстве.
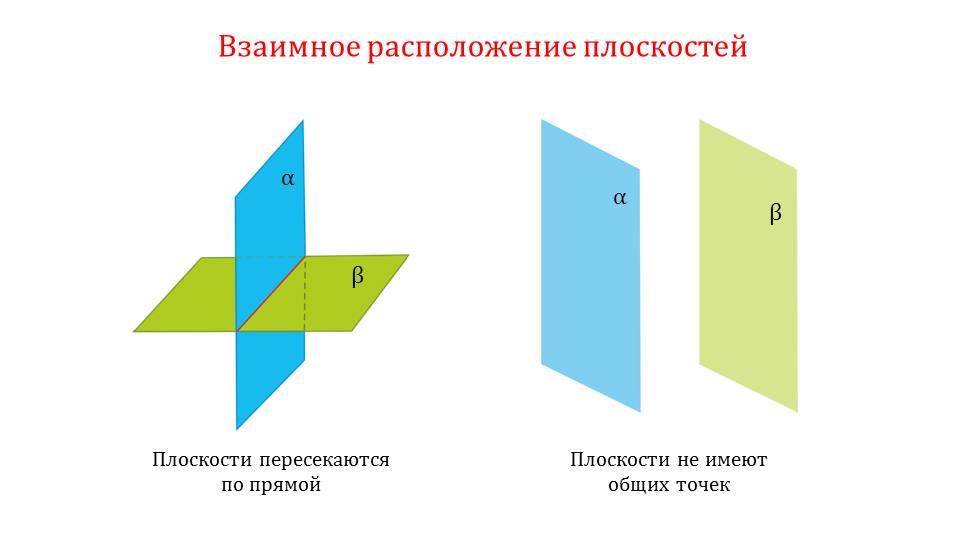
На первом слайде показывается два варианта расположения плоскостей альфа и бета в пространстве. В первом случае они имеют общую прямую, во втором – нет. Плоскости условно обозначены через параллелограммы.

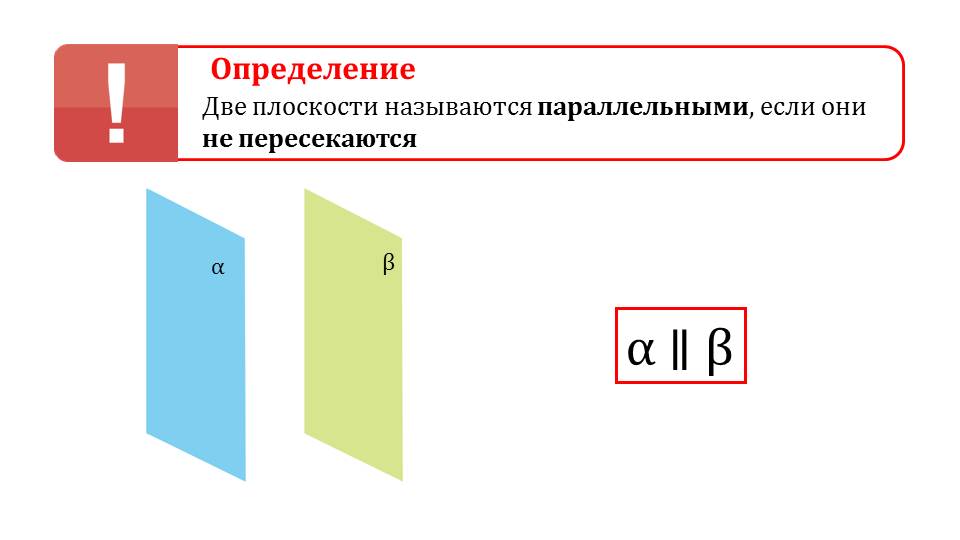
Плоскости, которые не имеют общих точек и прямых, называются параллельными. На следующем слайде видим иллюстрацию, демонстрирующую две плоскости альфа и бета, которые не пересекаются.
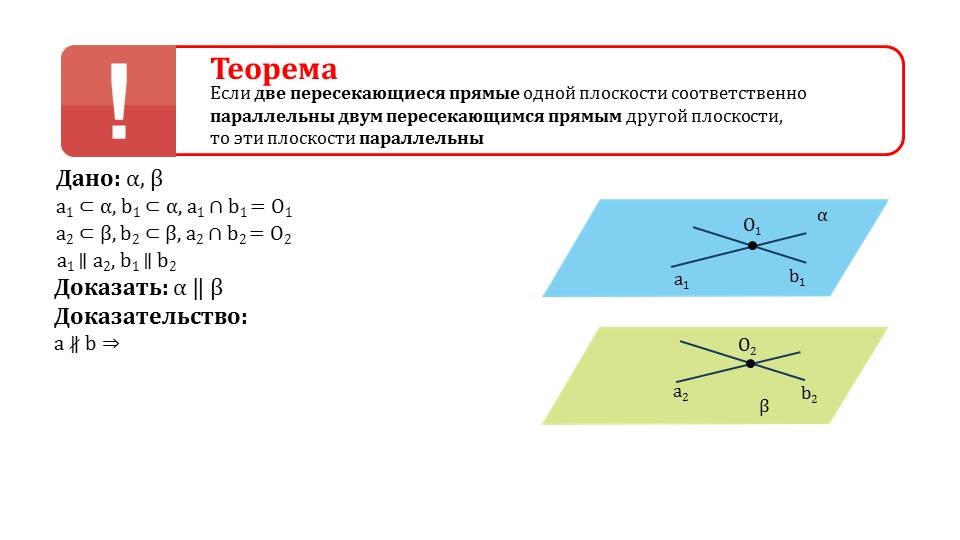
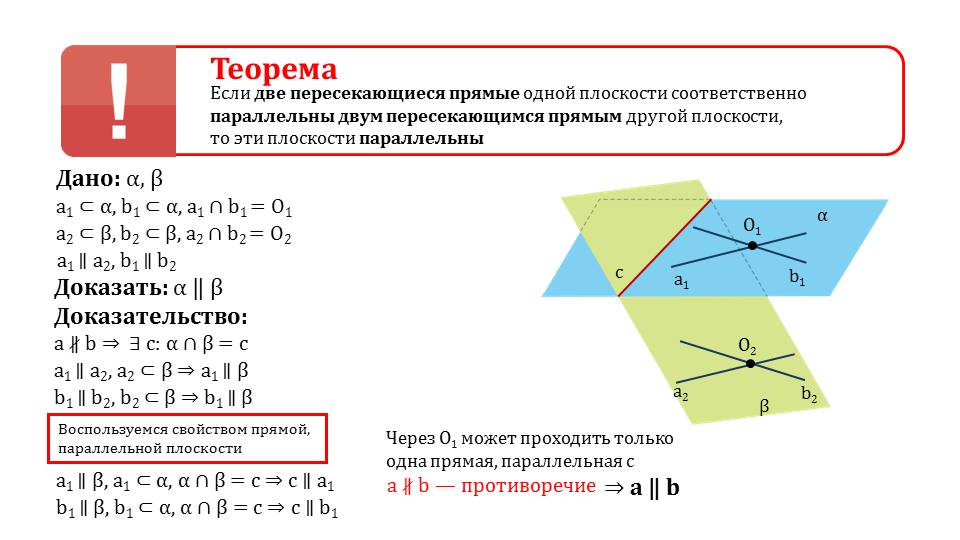
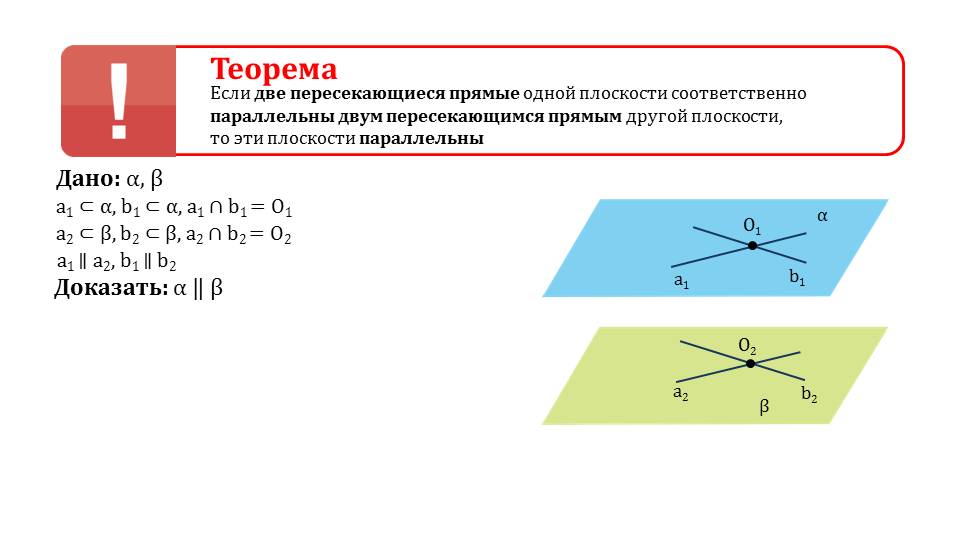
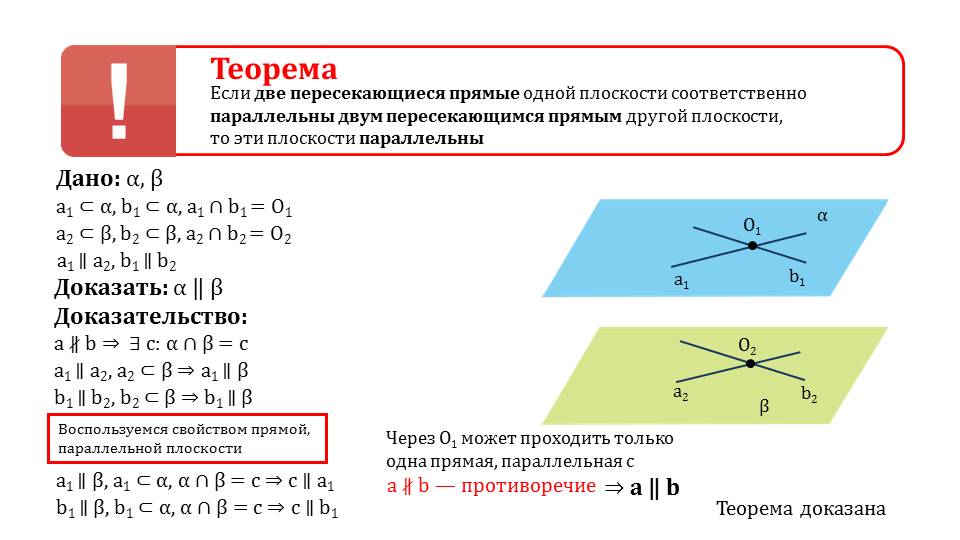
Существует признак, по которому можно определить параллельность некоторых плоскостей в пространстве. Гласит теорема о том, что если две некоторые прямые, лежащие на одной плоскости и являющиеся пересекающимися будут параллельны двум иным пересекающимся прямым, лежащим на иной плоскости. Так как это утверждение не является аксиомой, оно требует доказательства. На следующих слайдах оно и выводится, сопровождается иллюстрациями и подробныим объяснениями. Лучше просмотреть данные слайды вместе с учителем.
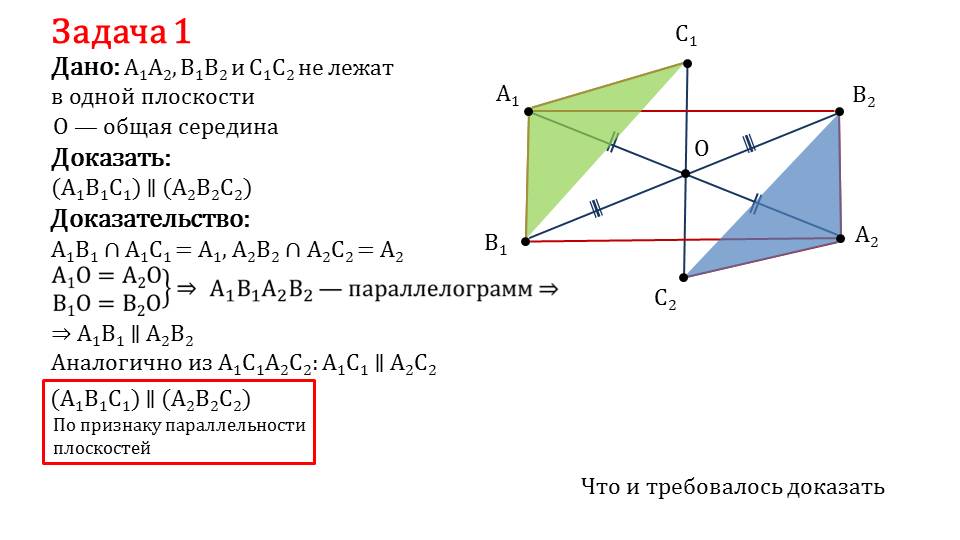
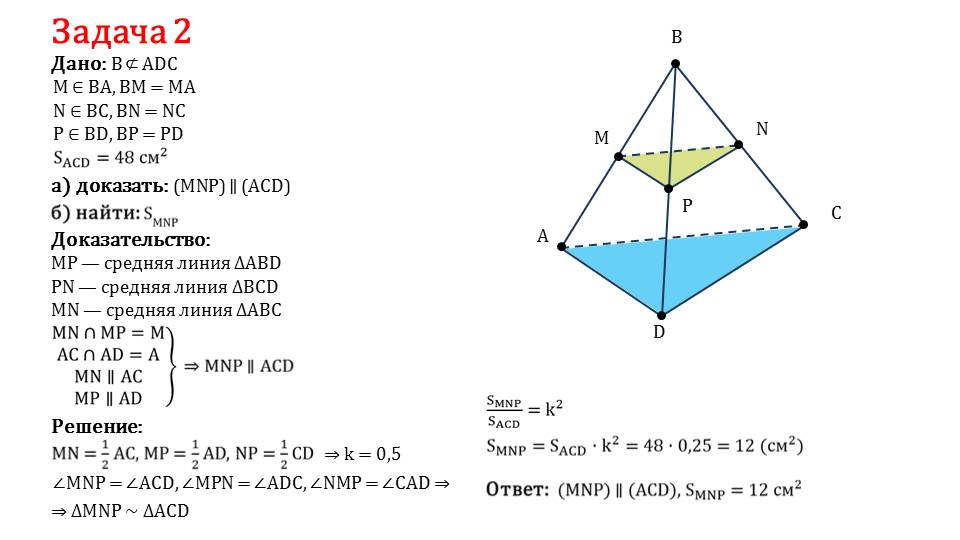
Далее в обучающем ресурсе рассматриваются задачи. Если понять суть их решения, то можно справиться и с домашним заданием.
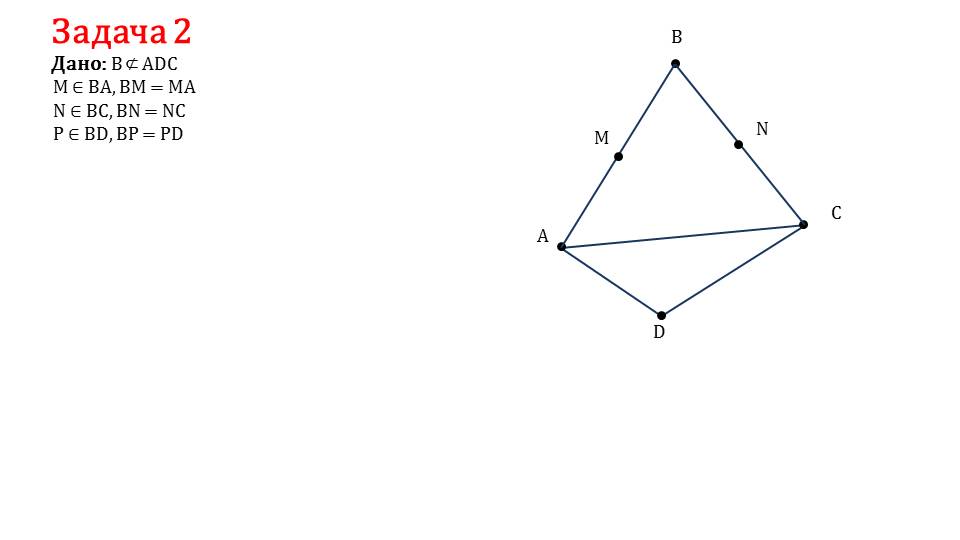
Благодрая данной презентации урок, проведенный в школе, станет более инересным и наглядным. Готовые иллюстраиции помогут лучше освоить материал. Наглядно оформленные определения и теоремы помогут учителю сэкономить время.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 7341 |
| Номер материала | 882 |