
Презентация "Параллельность прямой и плоскости"

Краткое описание документа:
После того, как школьники изучили тему «Параллельность прямых в пространстве», самое время рассмотреть параллельность прямой по отношению к плоскости. Эта тема также важна. Теоремы, которые будут изучены в данной презентации, пригодятся для решения различного рода задач в стереометрии. Пропустив данную тему, будет тяжело понять иные темы и практические задачи.
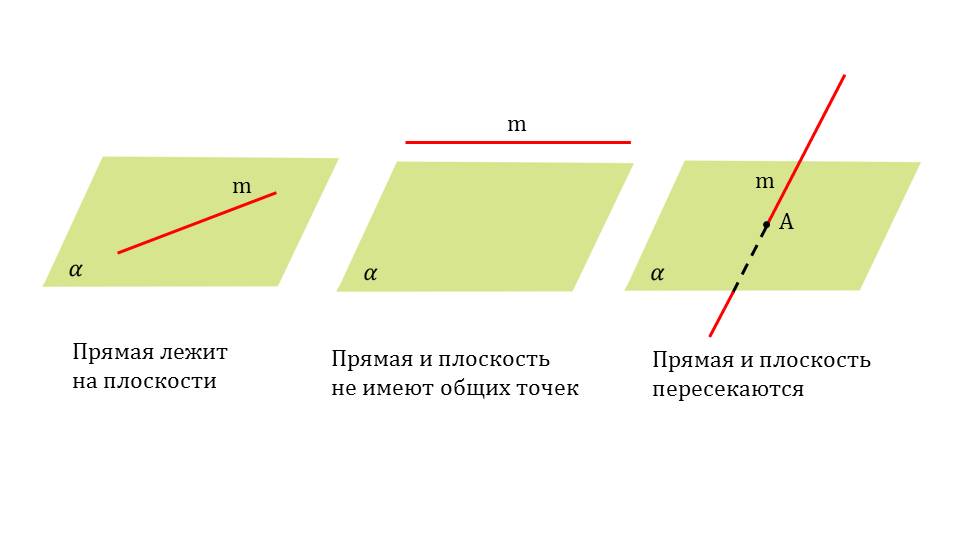

Какими могут быть прямые по отношению к плоскости? Во-первых, они могут их пересекать, во-вторых – они могут не иметь никаких общих точек, и в третьих, прямая может лежать непосредственно на плоскости. Эти три случая рассматриваются на первом слайде данного электронного обучающего ресурса. Приведены и иллюстрации к ним, которые демонстрируют все случаи.

В каком же из этих случаев прямая и плоскость будут параллельны? Определению параллельности прямой по отношению к плоскости посвящен следующий слайд. Оно выделено в специальный блок и его будет легко запомнить.
Так как довольно часто будет необходимость применять данное понятие, на следующей странице приводится обозначение. Оно гласит о том, что прямая А параллельна плоскости альфа.
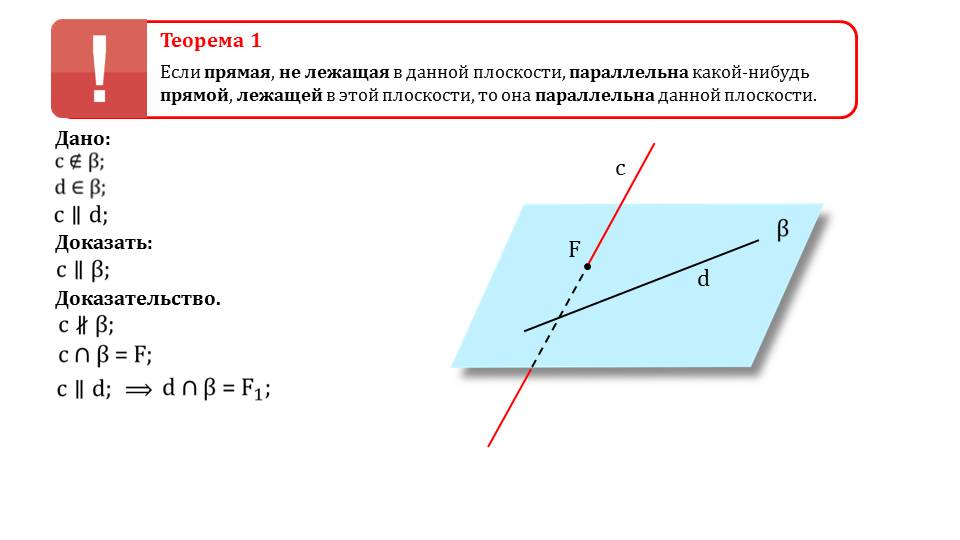
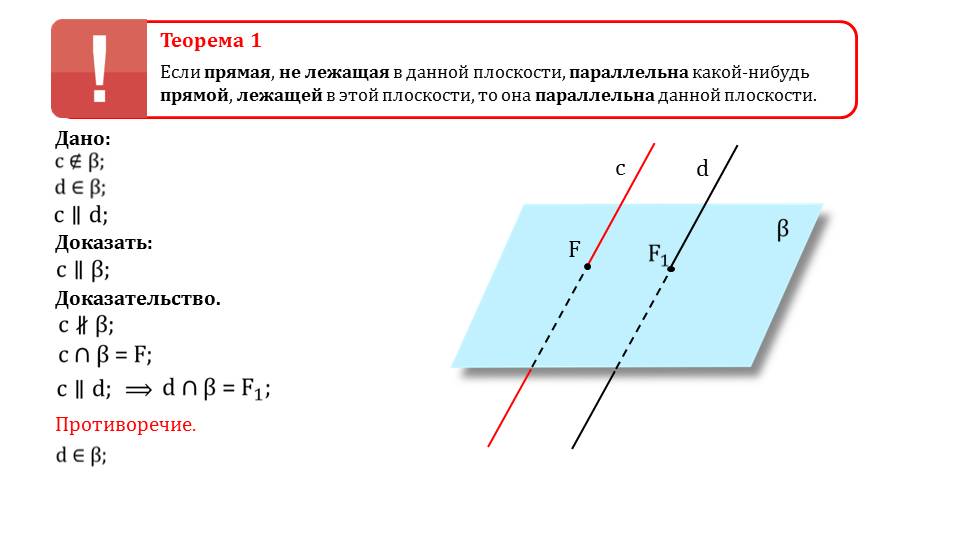
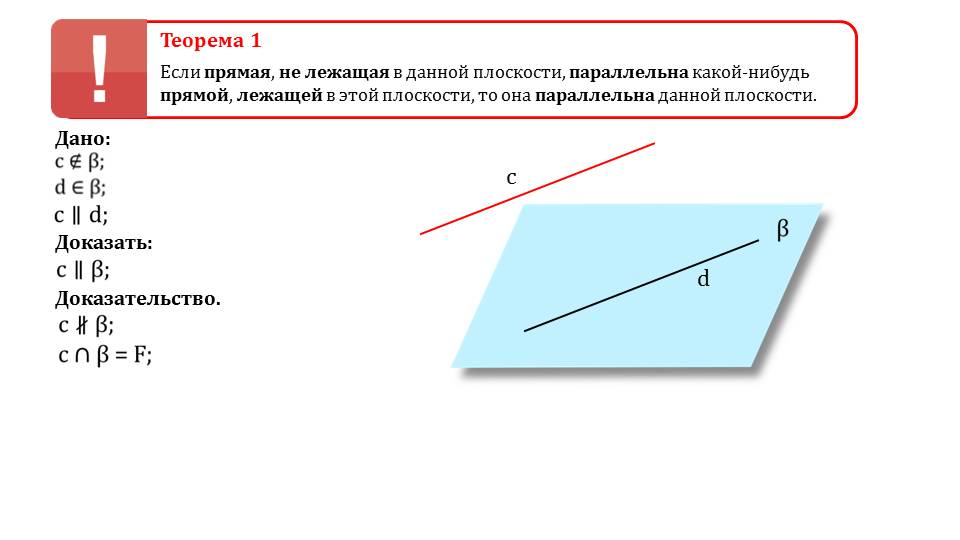
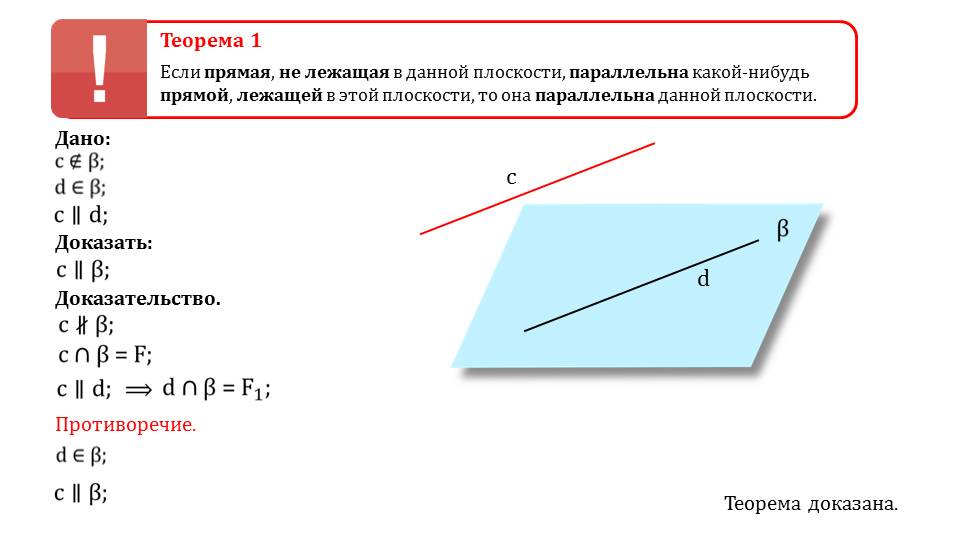
Если некоторая прямая будет параллельна иной прямой, которая лежит на плоскости, то первая прямая будет параллельна непосредственно плоскости. Об этом гласит первая теорема в данной презентации. Чтобы не осталось никаких неясностей, приводится несложное доказательство, которое можно будет с легкостью разобрать с учителем или репетитором. Доказывается теорема методом от противного, что является часто используемым приемом во многих случаях. Школьники к нему уже должны были бы привыкнуть и понимать.
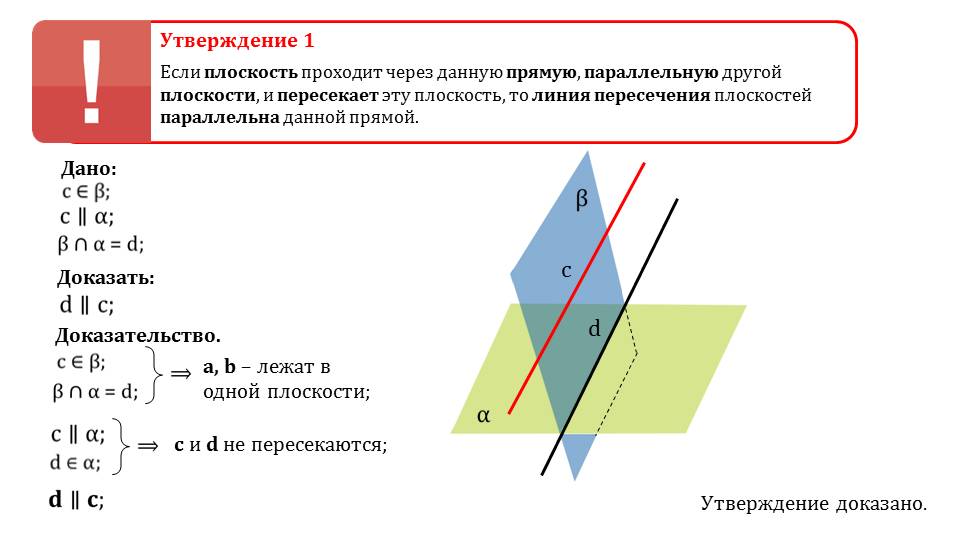
Путь имеем прямую и некоторую плоскость, которая параллельна ей. Если через данную прямую провести пересекающую плоскость с имеющейся плоскостью, то прямая пересечения и изначальная прямая будут параллельны. Это утверждение требует доказательства, ведь не является аксиомой. Доказательство не является объемным и не составит никакой сложности в понимании.
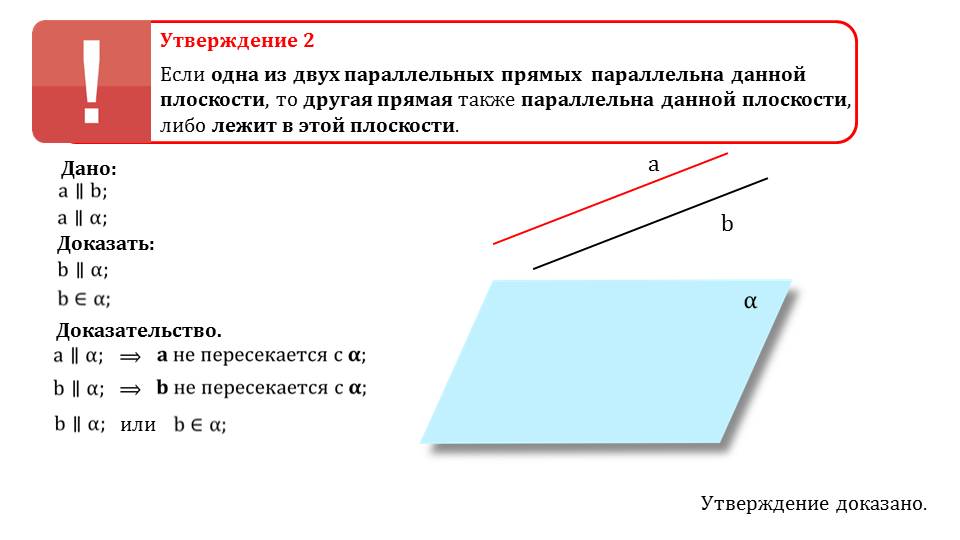
Если известно, что имеются две параллельные прямые, одна из которых параллельна, в свою очередь, с плоскостью, то эти прямые должны быть либо параллельно друг с другом, либо одна из них должна лежать на плоскости.
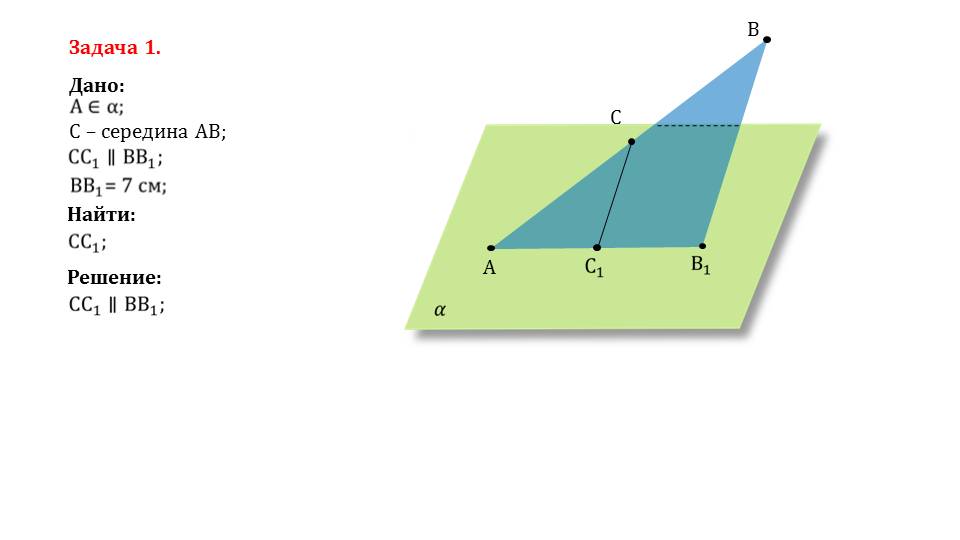
Далее предлагается рассмотреть две практические задачи, для решения которых необходимо использовать изученные теоремы. Они не являются сложными, однако потребуют время для размышления и понимания.
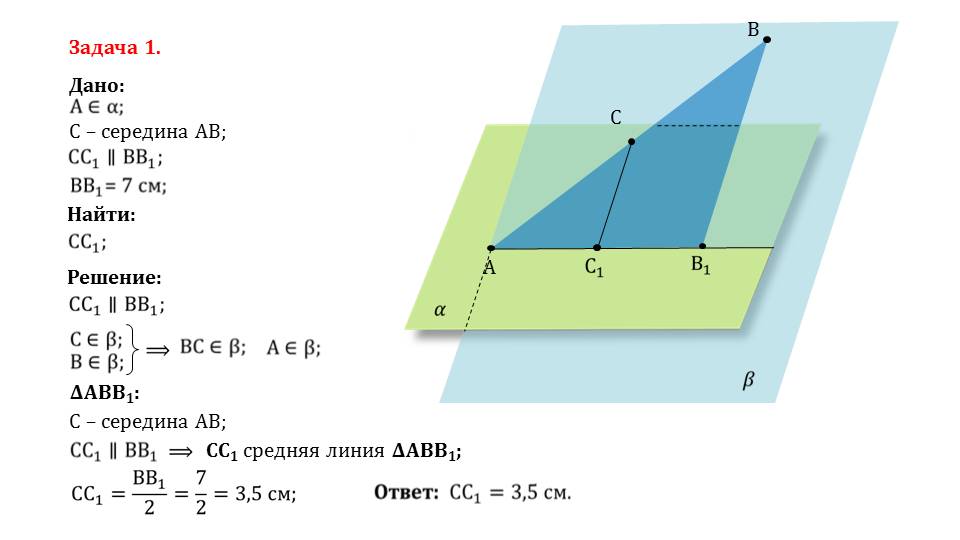
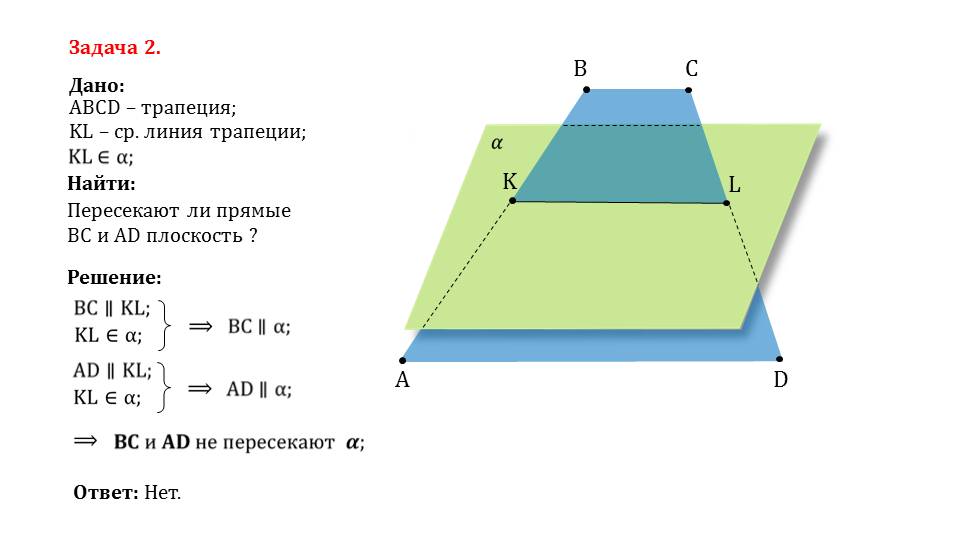
Просмотреть и разобрать презентацию можно во время урока вместе с учителем. Если он грамотно все прокомментирует, то школьникам станет понятен данный урок и запомнится на долгое время, не будут возникать проблемы при выполнении домашней работы, написании самостоятельных и контрольных работ.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 10880 |
| Номер материала | 878 |