
Презентация "Первый признак равенства треугольников"

Краткое описание документа:
В данном уроке речь пойдёт об основоположных определениях математики: теорема и её доказательство. Важно именно сейчас уяснить для себя необходимые термины, чтобы впоследствии легко ими оперировать. Однако для начала углубимся немного в историю происхождения самого понятия «теорема».


слайды 1-2 (Тема презентации "Первый признак равенства треугольников", теорема)
Слово «Теорема» пришло к нам из древнегреческого языка, и в переводе означает «взгляд, представление». Теорема является таким утверждением, для которого в границах определённой теории существует единственное уникальное доказательство. Что же называется «доказательством теоремы»? Это последовательное, поэтапное рассуждение о справедливости теоремы, исходя из заданных условий теоремы. Обычно доказательства теорем уже найдены.
За теоремы специалисты считать могут только наиболее важные утверждения. Те, которые не имеют большой ценности, известны в науке как предложения, условия или леммы. Порой, утверждения, близкие по значимости к теоремам могут, называться условиями, критериями и так далее. Следует также отметить такие понятия, как аксиома и гипотеза. Аксиома – это утверждения, для которых в рамках заданной теоремы доказательство не требуется. Гипотезами называют утверждения, для которых неизвестно, являются ли они теоремами.
слайд 3 (теорема)
Теперь перейдём к практическому значению нашей темы и попробуем проанализировать одну из теорем. В геометрии самый большой объём работы осуществляется с треугольником, потому что именно ему характерно множество свойств, признаков и прочих особенностей. Зная эти особенности, учащиеся с лёгкостью смогут решать задачи, сокращая время, потраченное на пример.
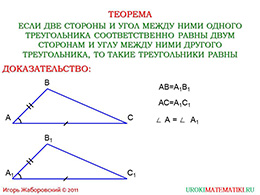
Всем произвольным треугольникам характерно три признака, но в данном уроке мы проанализируем и докажем первый из них (по углу и прилежащим сторонам).
Обратим внимание на формулировку теоремы и проговорим данные: в наших треугольниках «АВС» и «А1В1С1» равен угол «А» и «А1», а также стороны «АВ» и «А1В1», «АС» и «А1С1».
Наложим треугольники так, чтобы совместились вершины «А» и «А1» и углы «А» и «А1». Мы это можем сделать, потому что по условию углы равны. Угол и прилежащие стороны совместились, впрочем, как и остальные части треугольника. В результате получаем, что исходные треугольники являются равными. Это и является первым признаком равенства треугольников. Теорема полностью проанализирована, ну а доказательство совершено.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 3968 |
| Номер материала | 240 |