
Презентация "Пирамида"

Краткое описание документа:
Презентация «Пирамида»является наглядным пособием по данной теме. Свойства пирамиды как стереометрического тела сложно представлять на плоскости. Для изображения объемной фигуры недостаточно классной доски. На слайдах объемная фигура может изображаться, используя оттенки цветов, возможность вставлять рисунки, анимацию. Таким образом учителю легче добиться решения учебных задач. В ходе презентации углубляется понятие учеников о призме, рассматриваются ее элементы, формула для вычисления боковой поверхности, описывается решение задачи с применением полученных знаний.
В данной презентации использованы анимационные эффекты, помогающие представить построения так, что рассматриваемые свойства и понятия были более понятными для учеников. Использование анимации также помогает удерживать внимание учеников на изучаемом предмете. Для выделения текста формулировок используются отметки о важности информации, рекомендованной к запоминанию. Также способствует более быстрому запоминанию учебной информации выделение понятий и формулировок цветом.
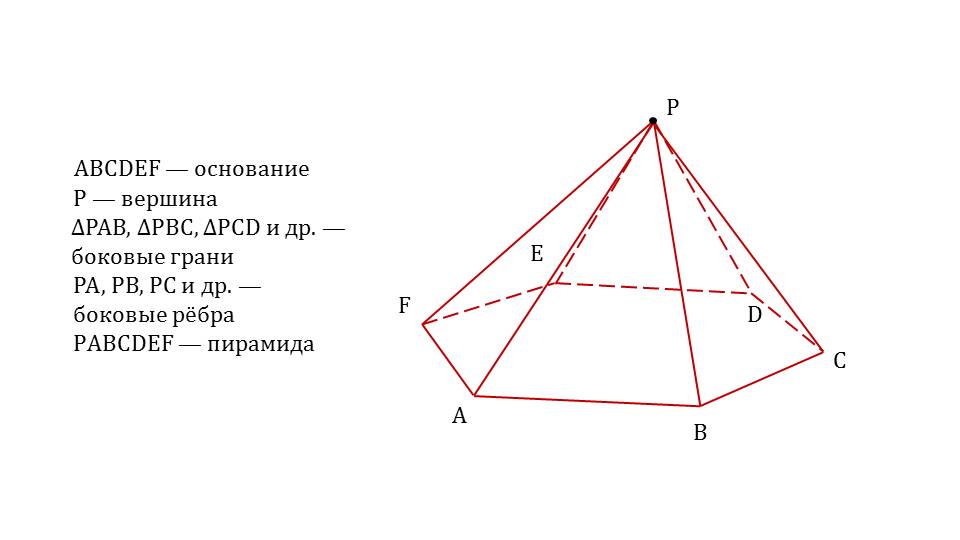
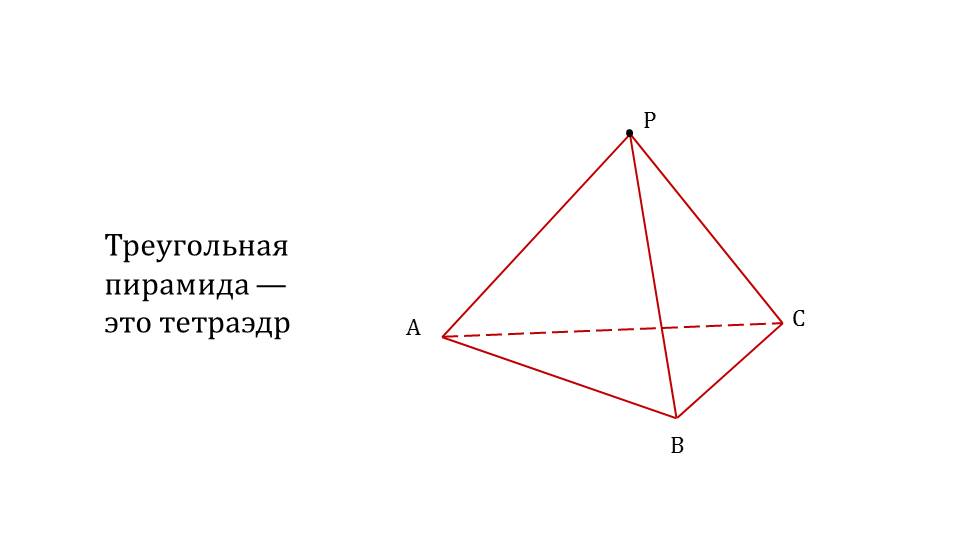
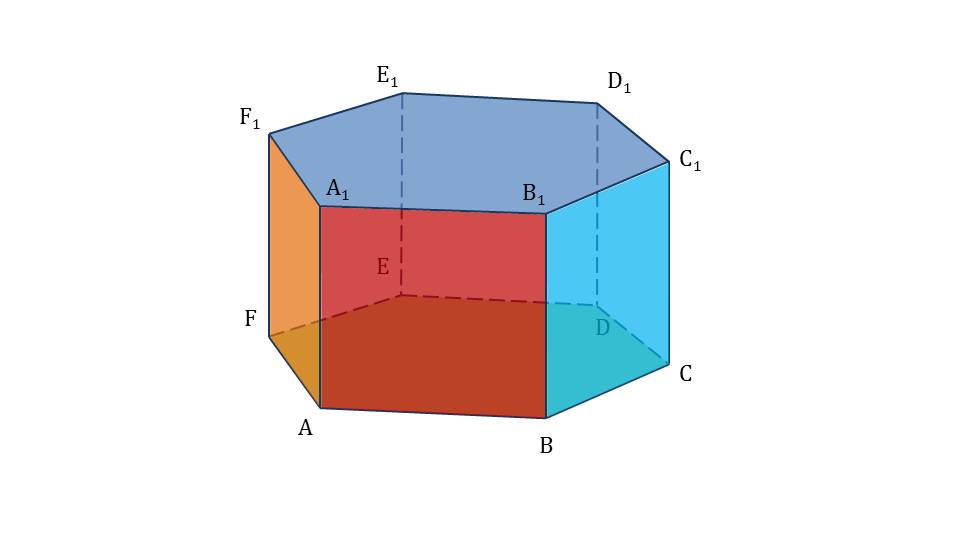
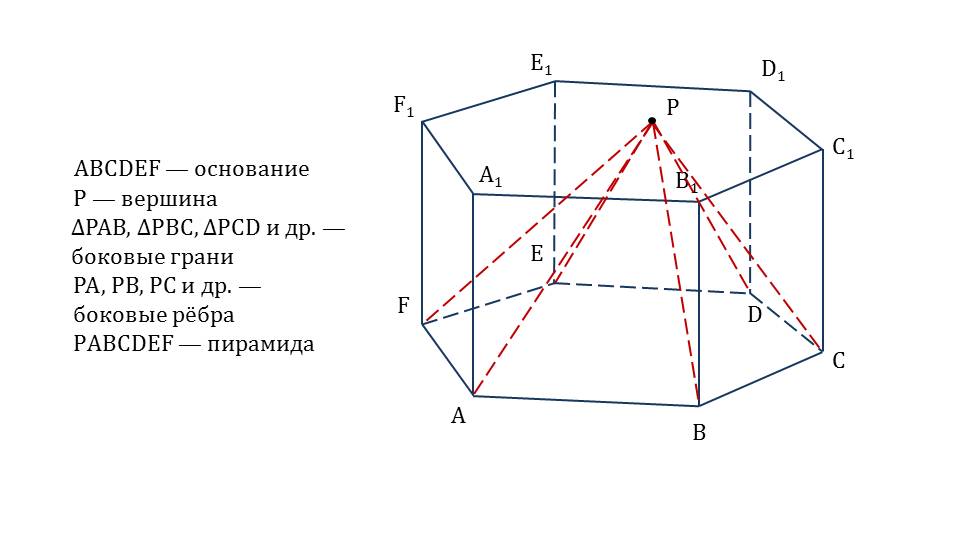
Демонстрация начинается с представления шестиугольной призмы ABCDEFA1B1C1D1E1F1, из которой сужением верхнего основания до точки Pобразуется пирамида PABCDEF. На слайде 2 в верхней плоскости призмы отмечена точка Р, с которой соединены каждая вершина многоугольника, лежащего в основании. Рядом с рисунком отмечаются элементы пирамиды ABCDEF – основание, точка Р – вершина, ΔРАВ, ΔРВС и т.д. – боковые грани, РА, РВ, РС и т.д. – боковые ребра. На следующем слайде с рисунка исчезает изображение боковых граней призмы, оставляя образованную таким образом пирамиду PABCDEF. На слайде 4 представлена самая простая пирамида – треугольная, в основании которой лежит треугольник АВС. Рядом с рисунком пирамиды ABCР отмечено, что треугольная пирамида – тетраэдр.
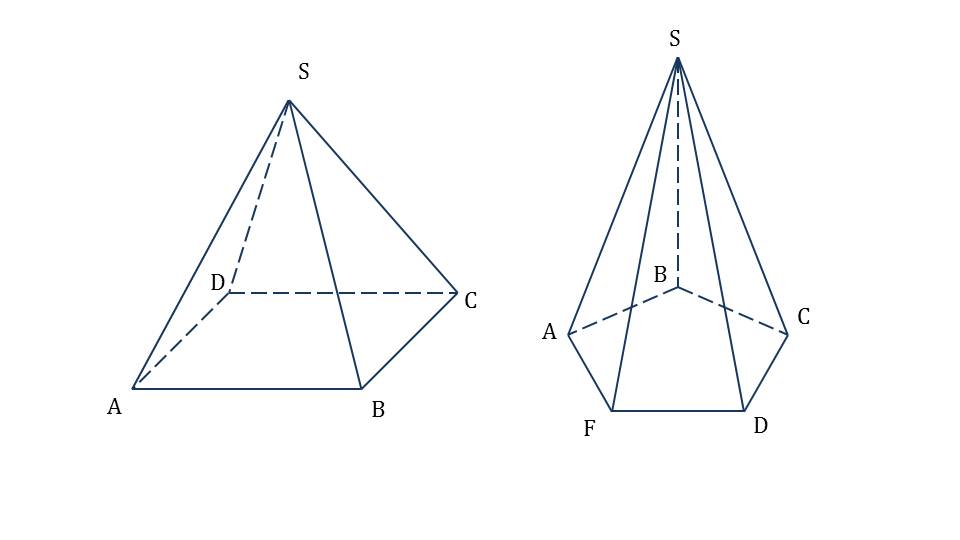
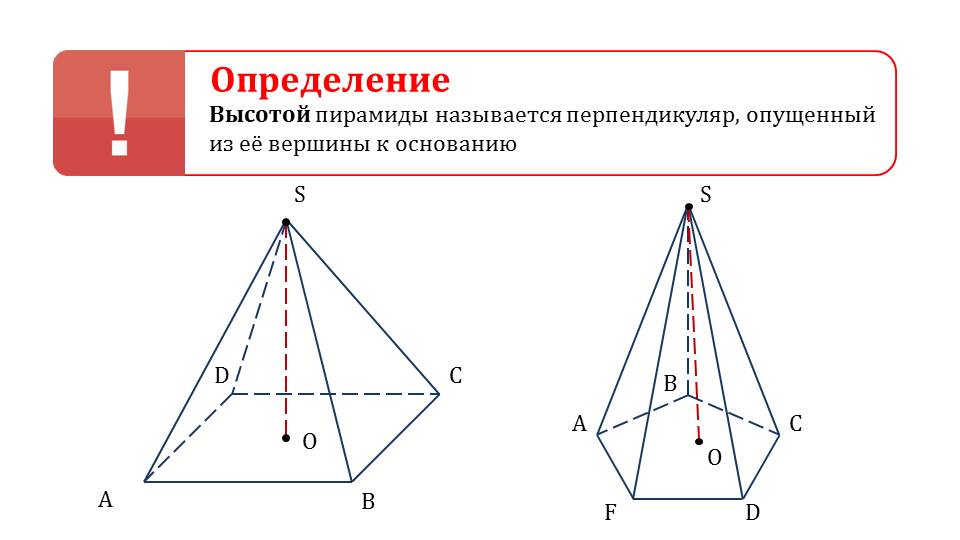
На слайде 5 представлены пирамиды ABCDSи ABCDFS. Первая пирамида – четырехугольная, а вторая – шестиугольная. В каждой из пирамид из вершины S на плоскость основания опускается перпендикуляр, который является высотой каждой пирамиды. Рядом с изображениями пирамид и отмеченными на них высотами сформулировано определение высоты пирамиды как перпендикуляра, опущенного от высоты к основанию.
На слайде 7 рассматривается, каким образом определяется площадь поверхности пирамиды. При этом отдельно выделяется площадь боковой поверхности пирамиды как площадь ее боковых граней, а также площадь всех граней – и боковых, и основания, как площадь полной поверхности Sполн.=Sбок.+Sосн.

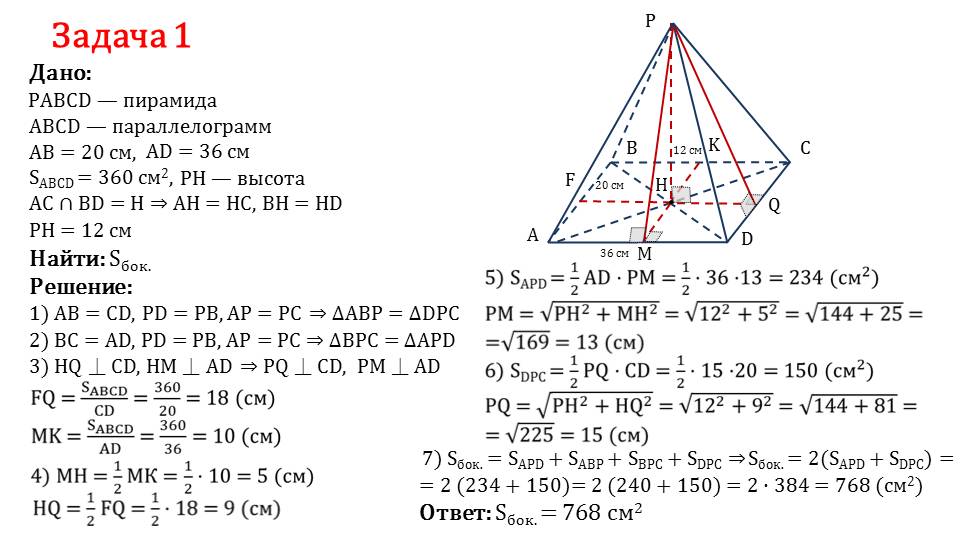
На последнем слайде описано решение задачи, в которой дана пирамида PABCD, основанием которой является параллелограмм ABCD со сторонами АВ=20 см, AD=36 см. Известна площадь параллелограмма SABCD=360 см2. Построена высота РН, а при пересечении диагонали делятся точкой их пересечения на равные части. При этом высота РН=12 см. Необходимо найти площадь боковой поверхности. Решение задачи начинается с использования свойств параллелограмма и равенства боковых ребер пирамиды для вывода о том, что треугольники ΔАВР и ΔDPC равны, а также треугольники ΔAPD и ΔВРС являются равными. Производятся вспомогательные построения высот треугольников, благодаря чему рассчитываются площади треугольников, образующих пирамиду. Затем определяется сумма всех найденных площадей Sбок.=768 см2.
Презентация «Пирамида» рекомендуется к применению на уроке геометрии как наглядный материал, повышающий эффективность обучения. Пособие может стать инструментом учителя, обучающего учеников дистанционно. Также пособие может помочь освоить тему ученику, изучающему ее самостоятельно или требующему дополнительных занятий.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 5420 |
| Номер материала | 901 |