
Презентация "Площадь квадрата"

Краткое описание документа:
В курсе уроков геометрии школьники сталкиваются с изучением различных геометрических фигур. Основными задачами при работе с ними является нахождение длин некоторых сторон фигур, отрезков при одномерном пространстве, если же речь идет о двумерном пространстве, то необходимо найти площадь. Также, позже школьники столкнуться с понятием объема при изучении стереометрии.
Данная же презентация посвящена изучению меры объектов в двумерном пространстве. Как было уже сказано, мерой является площадь. Площади различных фигур находятся по-разному, в зависимости от их свойств. Нет определенной формулы для всех фигур в геометрии.

слайды 1-2 (Тема презентации "Площадь квадрата", пример)
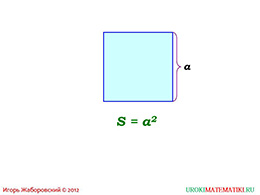
В данной презентации приступим к изучению площади простейшей фигуры – квадрата. На первом слайде можно увидеть формулировку и непосредственно фигуру.
Школьники уже знают, что такое квадрат, и какими свойствами он обладает. Разумеется, речь идет о равенстве его сторон, и о четырех прямых углах. Исходя из этого, формула нахождения площади квадрата является такой простой.
Ученик, изучающий данный материал, может записать эту формулу. Сторону квадрата в обучающем мультимедийном файле предлагается обозначить латинской буквой a, как это принято делать в большинстве случаев. Итак, площадь квадрата равен квадрату его стороны. Запомнить формулу не составит никакого труда.
слайды 3-4 (примеры)
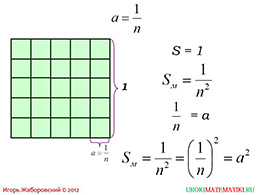
Откуда же появилась эта формула? Об этом можно узнать, перейдя на последующий слайд. Здесь можно увидеть квадрат, который условно разбит на n частей. В результате мы видим условную сетку. Если взять некоторый столбец из получившейся таблицы, то его можно выразить алгебраически в виде дроби. Этот столбец выражает нашу сторону.
Если запишем сумму площадей всех этих маленьких полученных единичных квадратов, то получим площадь всего квадрата. Таким образом, площадь будет равняться единице деленной на общее количество квадратов, то есть n, в квадрате. Так как 1/n = a, то сделав замену, изначально предложенную формулу площади квадрата.
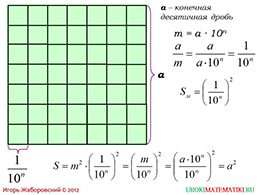
Чтобы школьники, изучающие данную тему, поняли лучше, предлагается рассмотреть сторону a как бесконечную десятичную дробь. Рассматриваем подробнее случай, при такой стороне. Выясним, что формула площади, в любом случае остается верной.
слайд 5 (пример)
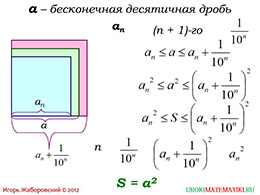
На следующем слайде предлагается рассмотреть случай, где а является бесконечной десятичной дробью. Если разобраться с содержимым на слайде, то можно выяснить, что при данном случае также получим доказательство верности нашей формулы.
Если данная презентация используется учителем для объяснения этой темы во время урока, то с целью закрепления материала, он может предложить школьникам решить практические примеры. После нескольких практических примеров, они, несомненно, запомнят данную формулу да долгие годы.
В дальнейшем школьники ознакомятся с нахождением площадей и других более сложных фигур, таких как прямоугольник, трапеция, треугольник и др. Не зная данную формулу не стоит переходить к изучению следующих уроков.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 3941 |
| Номер материала | 329 |