
Урок "Понятие площади многоугольника"

Краткое описание документа:
Площадь – это величина, характеризующая размер геометрической фигуры. Расположенный на плоскости многоугольник занимает какую-то ее часть. Размер этой части плоскости и будет равен площади многоугольника. Определение площадей геометрических фигур является одной из древнейших задач геометрии, которая и в настоящее время имеет важное практическое значение. Как и при всяком измерении какой-либо величины, при определении площади необходимы единицы измерения - такие меры, с которыми сравнивается площадь данной фигуры.
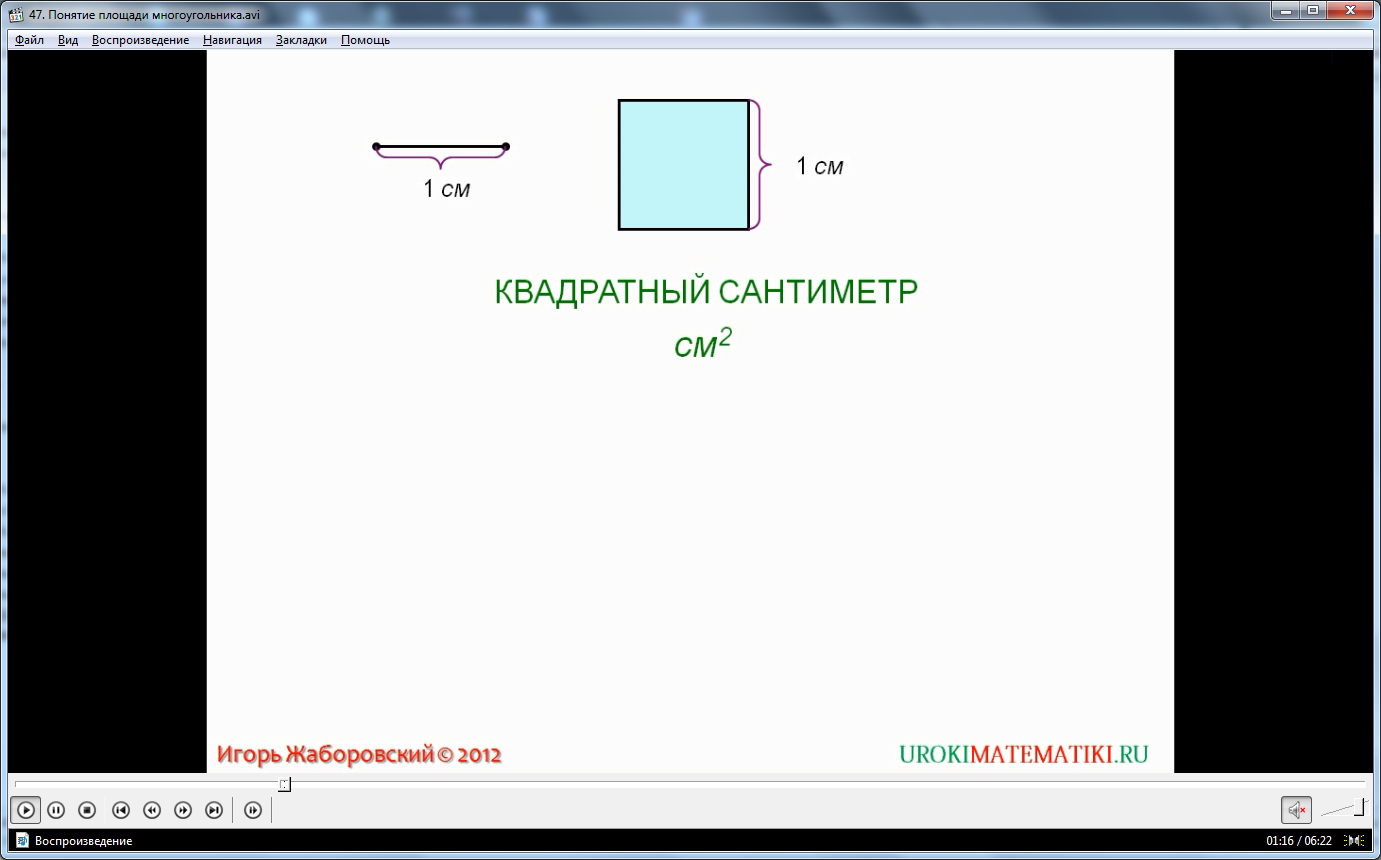
В предложенном видеоматериале единица измерения площади показана в виде квадрата со стороной, равной сантиметру. Эта мера называется квадратным сантиметром. В квадратных сантиметрах можно, например, выразить площадь многоугольника, построенного на тетрадном листе. Если сторона квадрата равна километру, то полученная единица измерения площади будет называться квадратным километром. В километрах квадратных выражают большие площади, например, площади стран и континентов. Квадрат, со стороной один миллиметр, называется квадратным миллиметром. В таких единицах измерения выражаются малые площади.
У, показанного на слайде этого видео урока, прямоугольника одна сторона равна двум сантиметрам, а, смежная с ней, сторона равна трем сантиметрам. Если на обеих сторонах прямоугольника от вершины отложить отрезки, равные одному сантиметру, и через точки деления провести прямые, как показано на слайде, то прямоугольник окажется разделенным на шесть квадратов, площадь каждого из которых равна одному квадратному сантиметру. Таким образом, площадь этого прямоугольника - шесть сантиметров квадратных.
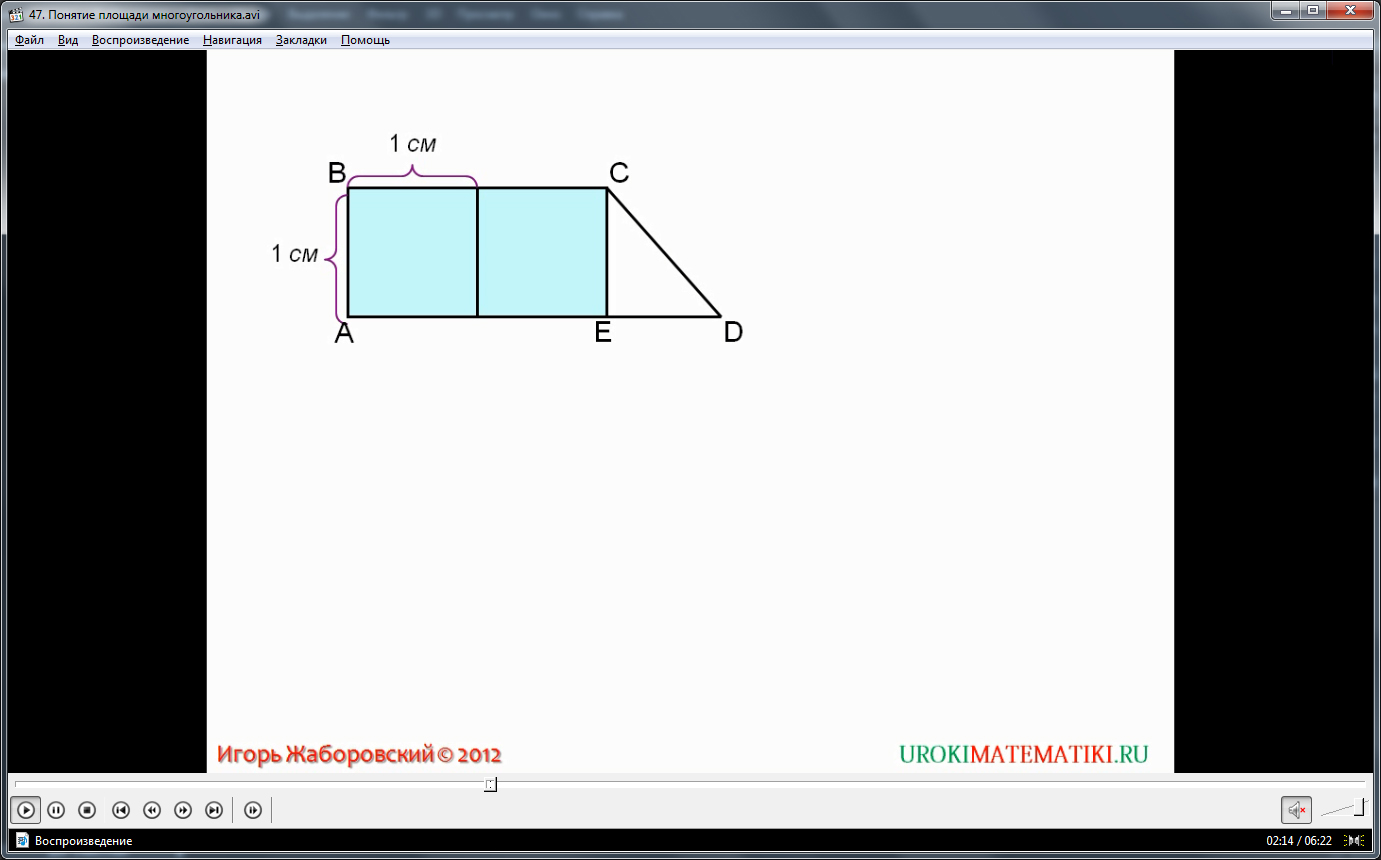
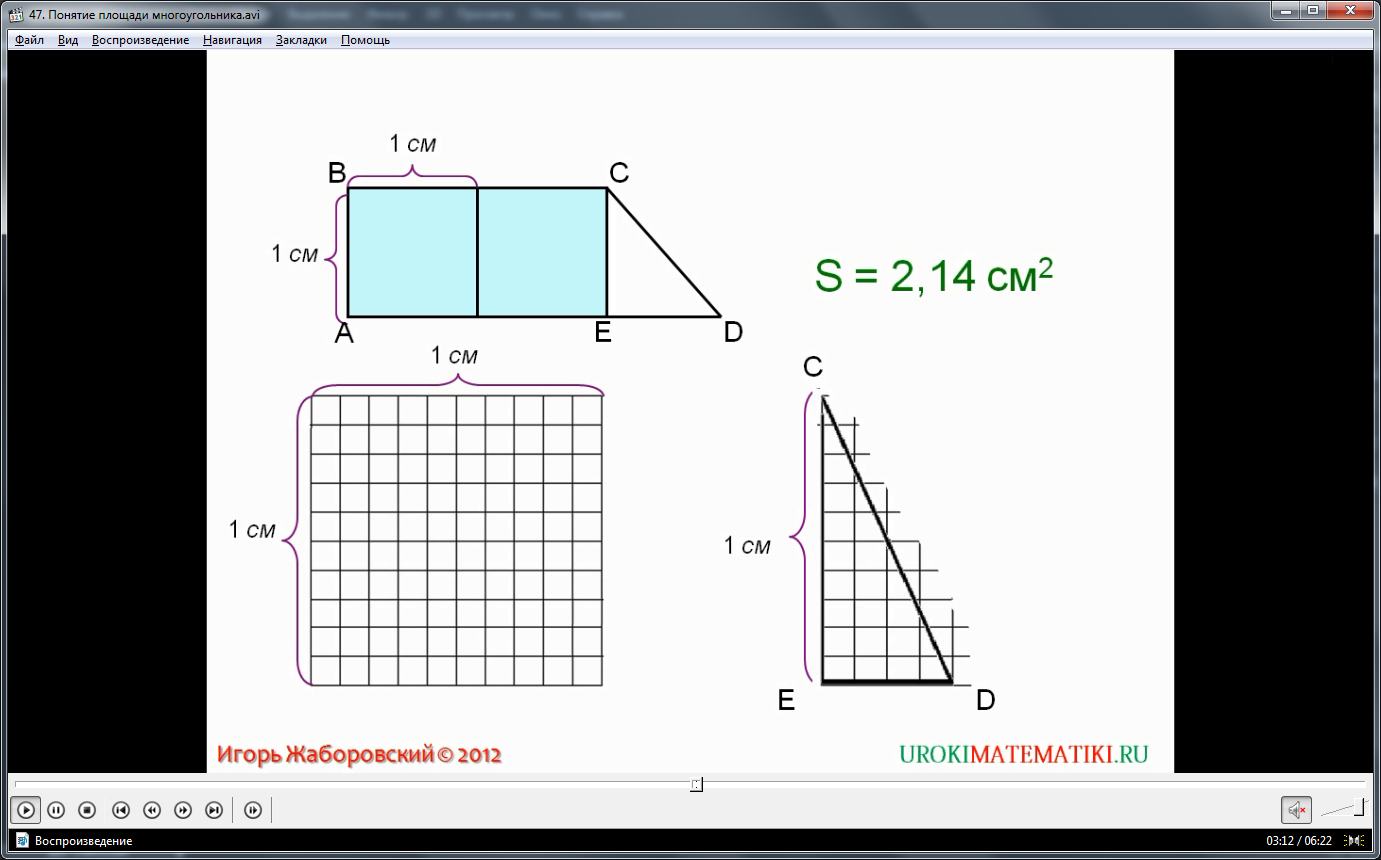
Следующая фигура, нахождение площади которой рассмотрено в видеоматериале, - трапеция. Как показано на слайде, трапецию можно представить состоящей из прямоугольника и треугольника. На прямоугольнике помещаются два квадрата, а значит его площадь - два сантиметра квадратных. Для определения площади треугольника нужно использовать более мелкие единицы. В видеоуроке квадрат разбит на сто частей – квадратов со стороной один миллиметр. На треугольнике помещаются четырнадцать целых таких частей. Таким образом, площадь показанной фигуры 2,14 сантиметров квадратных. Но на треугольнике помещаются еще и части мелких квадратов. Чтобы определить площадь треугольника более точно, нужно использовать еще более мелкие квадраты. На практике это неудобно, потому получены специальные формулы для определения площадей некоторых фигур.
При определении площадей многоугольников исходят из свойств их площадей.
Площадь - величина всегда положительная.
У равных многоугольников площади тоже равны.
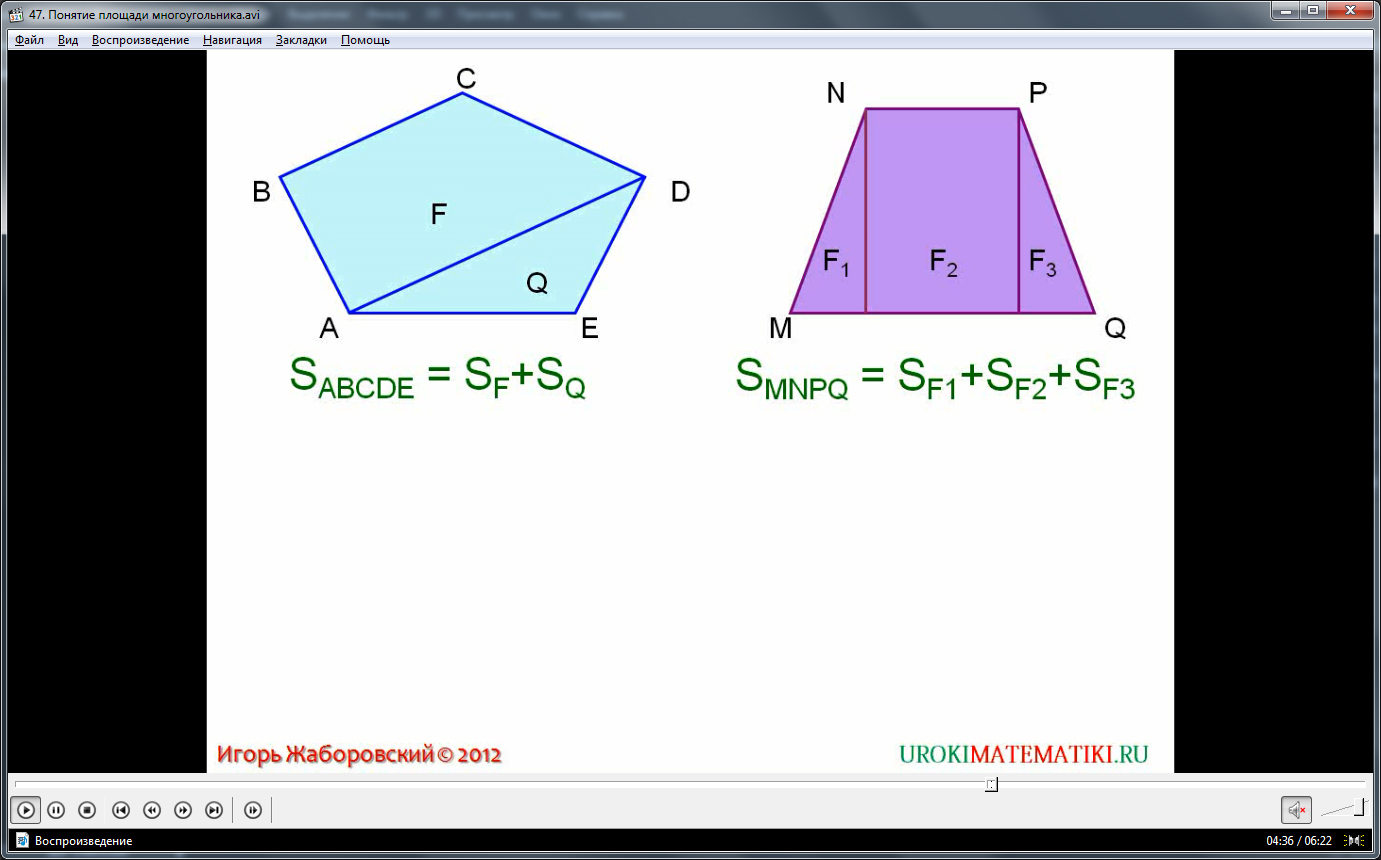
Любой сложный многоугольник можно представить составленным из более простых многоугольников. В этом случае его площадь равна сумме площадей, входящих многоугольников. Например, пятиугольник в видеоматериале состоит из четырехугольника (трапеции) и треугольника, а четырехугольник трапеция состоит из прямоугольника и двух треугольников. В обоих случаях, согласно только что приведенному свойству, площади многоугольников ABCDE и MNPQ равны сумме площадей фигур, из которых они состоят.
Следующее вполне очевидное положение состоит в том, что площадь квадрата равна квадрату его стороны. На слайде видеоурока показан квадрат, стороны которого равны 2,1 сантиметра. Его площадь равна 4,41 сантиметра квадратных, численно это квадрат числа 2,1.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 6144 |
| Номер материала | 585 |