
Презентация по алгебре на тему "Квадратичная функция" (9 класс)
















Описание презентации по отдельным слайдам:
Эпиграф к уроку: «Предмет математика настолько серьезен, что полезно не упустить случая сделать его немного занимательнее». Блез Паскаль
Укажите те функции, которые являются квадратичными: А) у = 5х+1; Б) у = 3х²-1; В) у = -2х²+х+3; Г) у = x³+7x-1; Д) у = 4х²; Е) у = -3х²+2х.
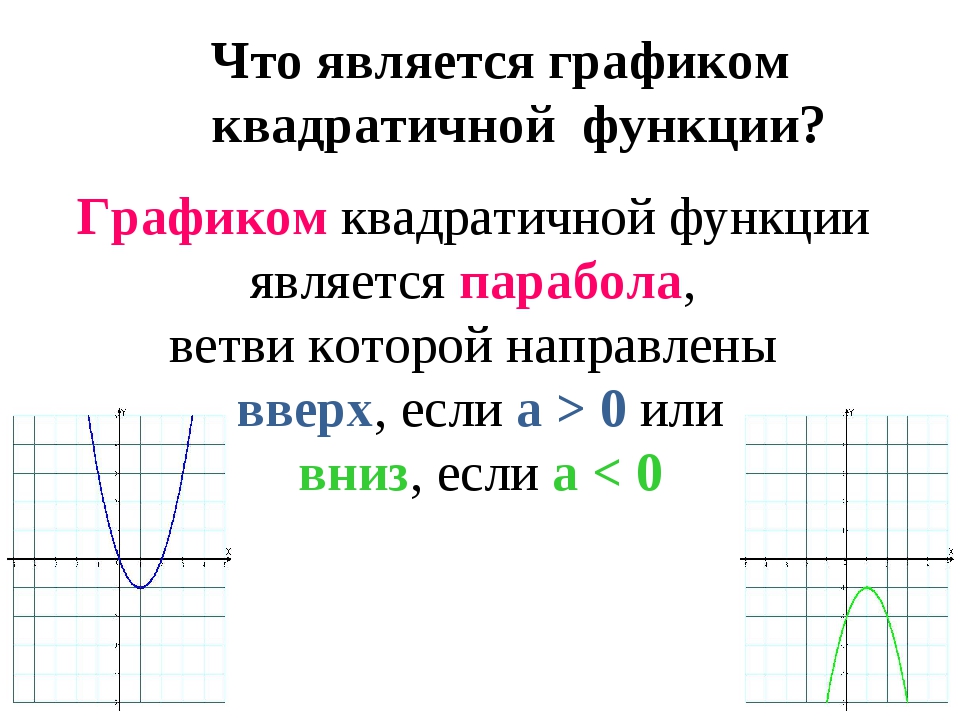
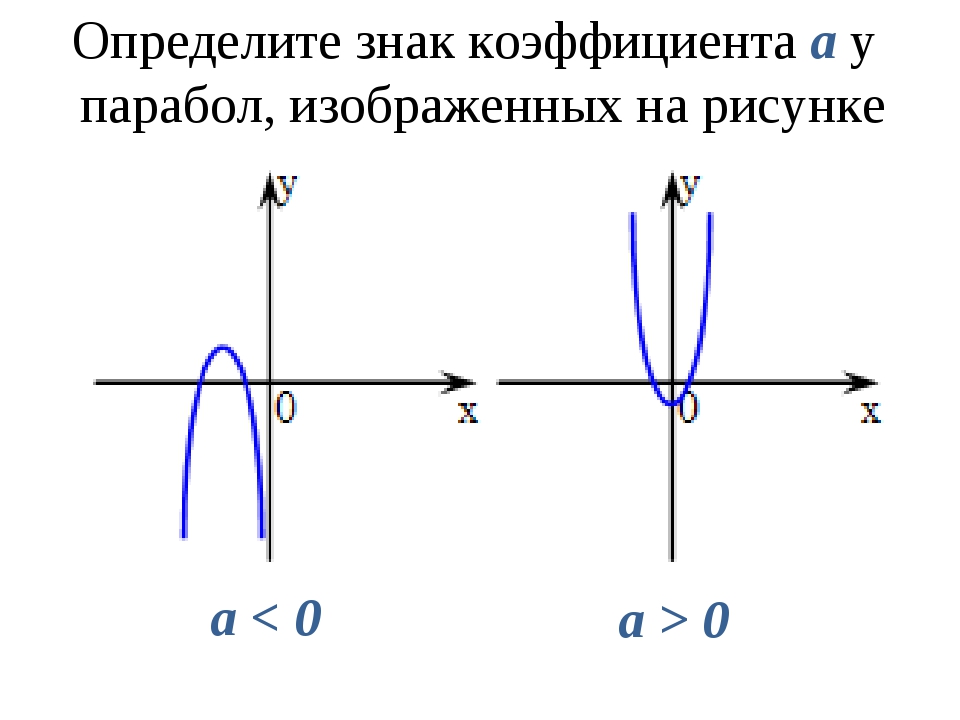
Графиком квадратичной функции является парабола, ветви которой направлены вверх, если а > 0 или вниз, если а < 0 Что является графиком квадратичной функции?
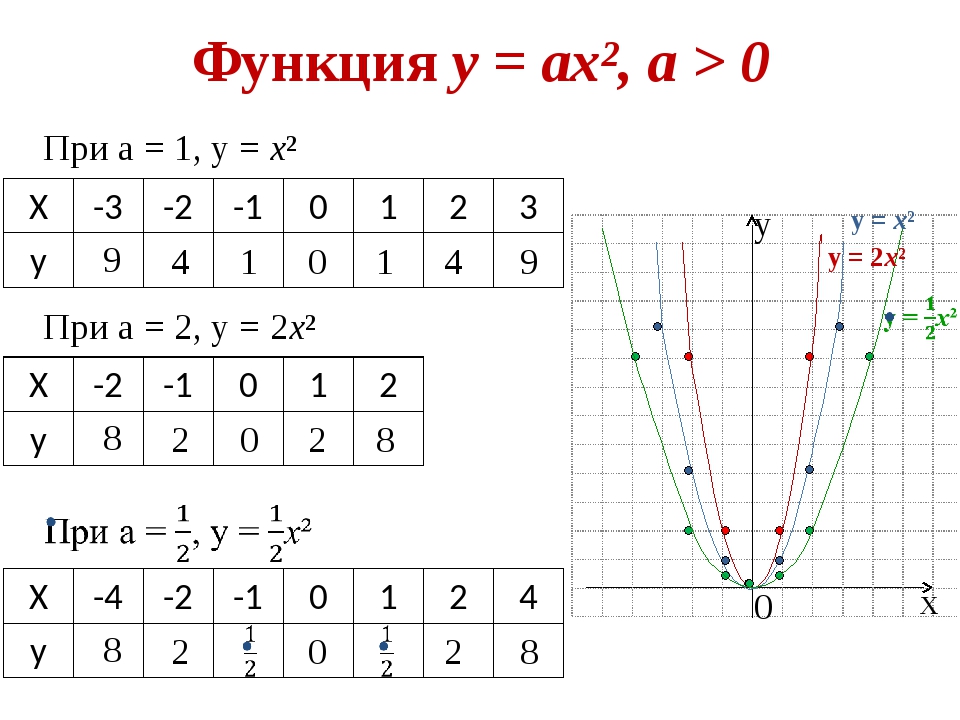
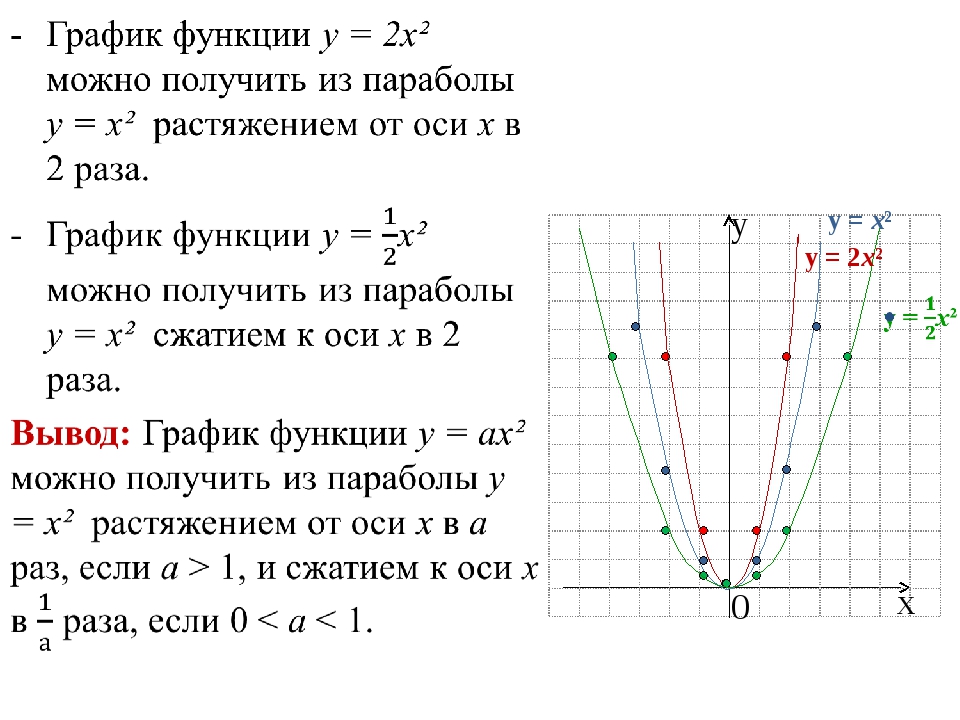
Функция у = ах², а > 0 При а = 1, у = х² х у 0 9 4 1 0 1 4 9 При а = 2, у = 2х² 8 2 0 2 8 8 2 0 2 8 у = х² у = 2х² Х -3 -2 -1 0 1 2 3 у Х -2 -1 0 1 2 у Х -4 -2 -1 0 1 2 4 у
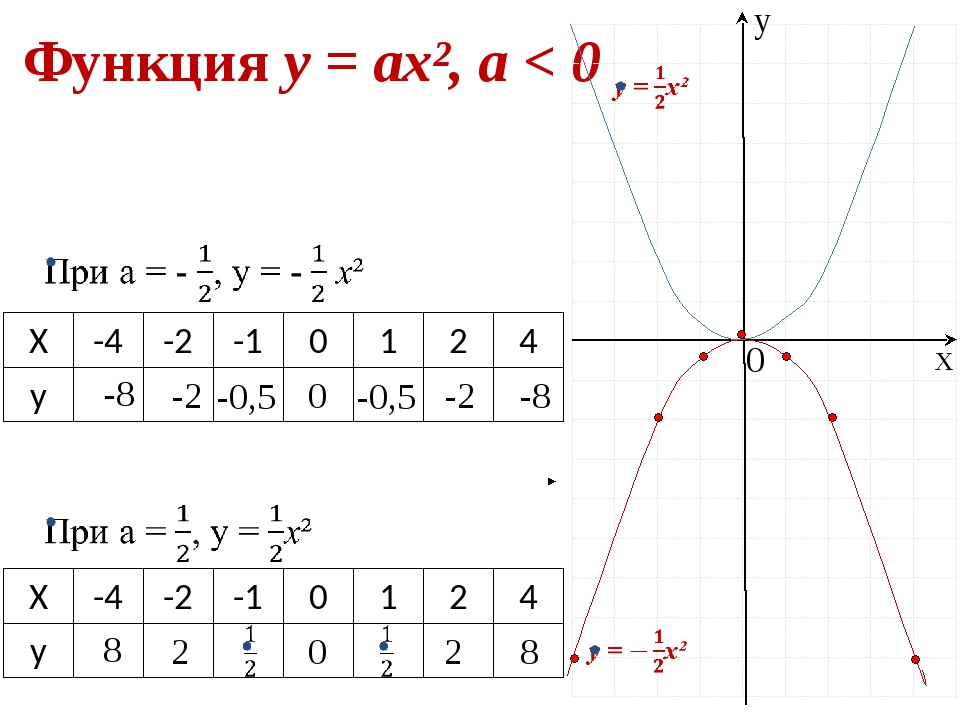
Функция у = ах², а < 0 -8 -2 0 -2 -8 -0,5 -0,5 х у 0 8 2 0 2 8 Х -4 -2 -1 0 1 2 4 у Х -4 -2 -1 0 1 2 4 у
График линейной функции Линейной называется функция, которая задаётся формулой вида у = кх + в, где х – независимая переменная, к и в – некоторые числа
y = 2x + 2 y = - x - 2 y = 2x - 6 y = 2x y = -2x + 3 1 2 3 4 5 6 y = 2x - 1 Сопоставьте номер графика и формулу
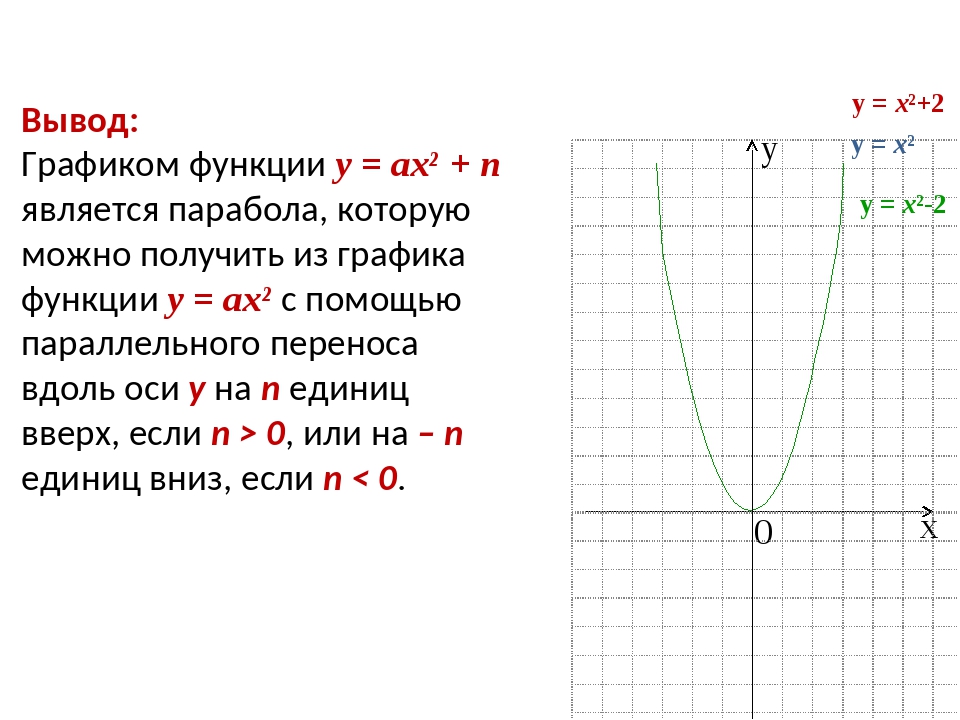
Функция у = ах² + n х у 0 у = х² При а = 1, у = х² 9 4 1 0 1 4 9 При а = 1, у = х² + 2 11 6 3 2 3 6 11 При а = 1, у = х² - 2 7 2 -1 -2 -1 2 7 у = х²+2 у = х²-2 Х -3 -2 -1 0 1 2 3 у Х -3 -2 -1 0 1 2 3 у Х -3 -2 -1 0 1 2 3 у
Вывод: Графиком функции у = ах² + n является парабола, которую можно получить из графика функции у = ах² с помощью параллельного переноса вдоль оси у на n единиц вверх, если n > 0, или на – n единиц вниз, если n < 0. х у 0 у = х² у = х²+2 у = х²-2
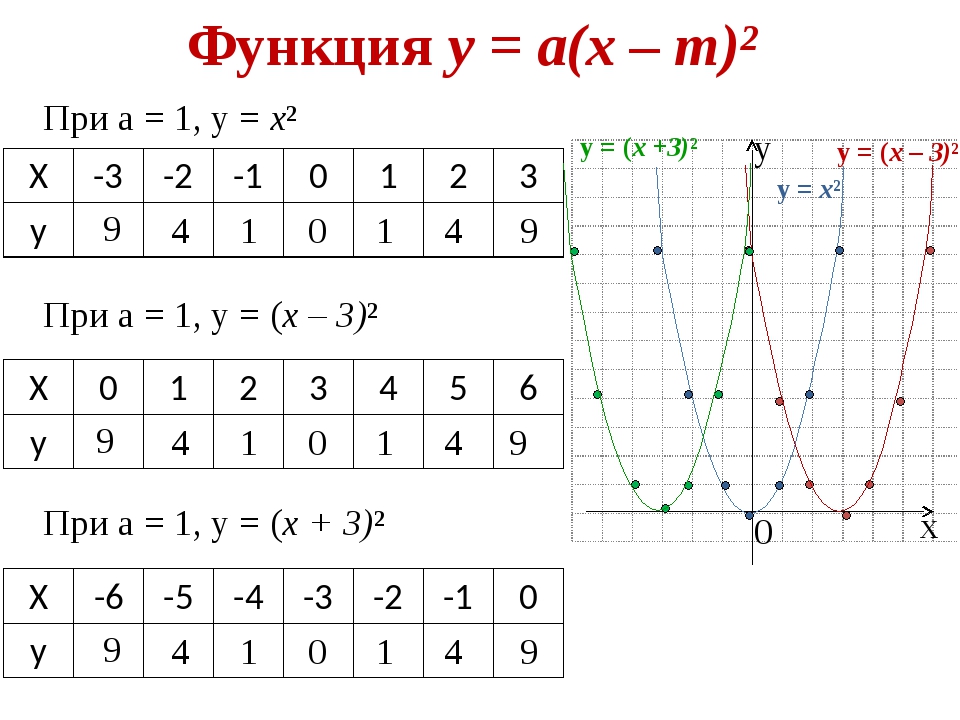
Функция у = а(х – m)² х у 0 у = х² При а = 1, у = х² 9 4 1 0 1 4 9 При а = 1, у = (х – 3)² 9 4 1 0 1 4 9 При а = 1, у = (х + 3)² 9 4 1 0 1 4 9 у = (х – 3)² у = (х +3)² Х -3 -2 -1 0 1 2 3 у Х 0 1 2 3 4 5 6 у Х -6 -5 -4 -3 -2 -1 0 у
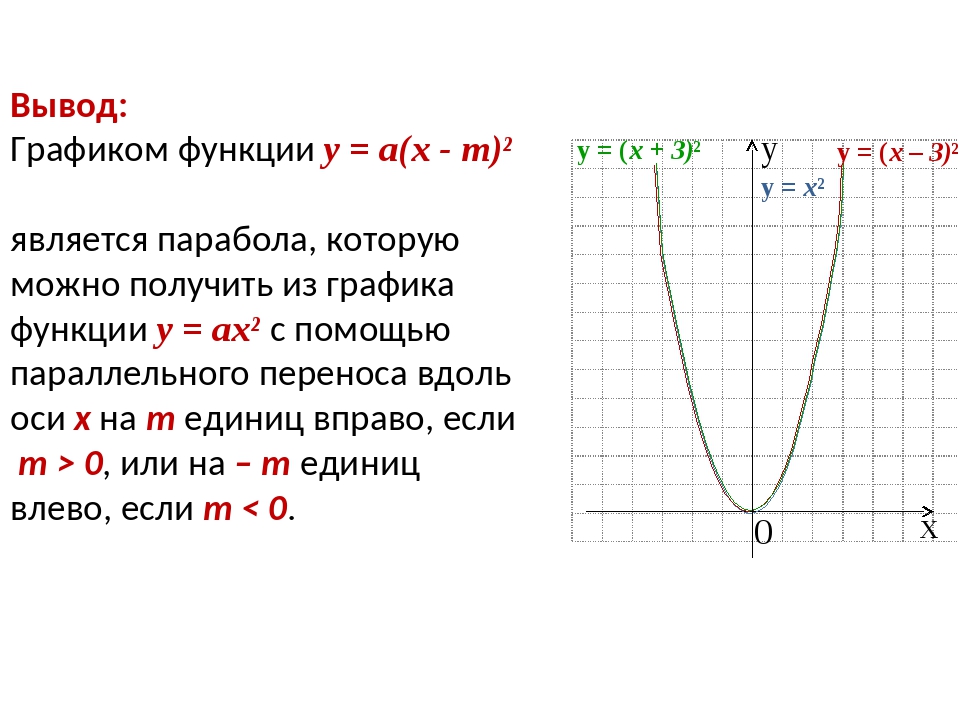
Вывод: Графиком функции у = а(х - m)² является парабола, которую можно получить из графика функции у = ах² с помощью параллельного переноса вдоль оси x на m единиц вправо, если m > 0, или на – m единиц влево, если m < 0. х у 0 у = х² у = (х – 3)² у = (х + 3)²
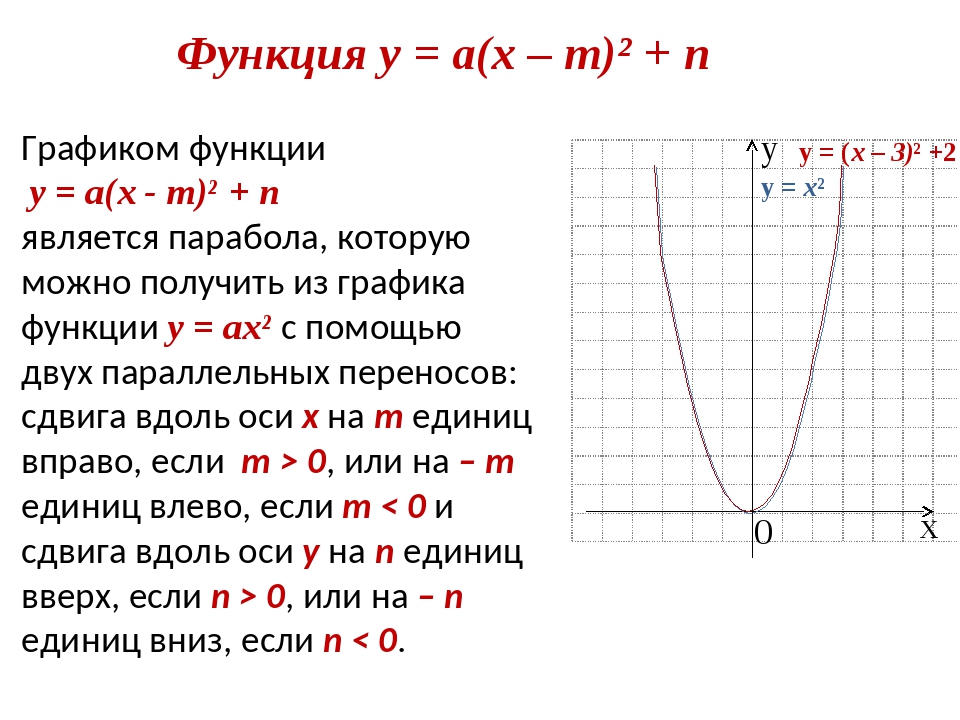
Функция у = а(х – m)² + n Графиком функции у = а(х - m)² + n является парабола, которую можно получить из графика функции у = ах² с помощью двух параллельных переносов: сдвига вдоль оси x на m единиц вправо, если m > 0, или на – m единиц влево, если m < 0 и сдвига вдоль оси у на n единиц вверх, если n > 0, или на – n единиц вниз, если n < 0. х у 0 у = х² у = (х – 3)² +2
Работа с учебником Упр. 106, 107, 110, 116 Домашняя работа: П. 5,6 – знать № 108, 112, 113

| Автор | |
|---|---|
| Дата добавления | 03.11.2018 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 3984 |
| Номер материала | 5901 |