
Презентация по математике Болдыревой Е.(11 "Б" класс) на тему " Задания для подготовки к ЕГЭ по математике (базовый уровень, задания №11-20)"


































































Описание презентации по отдельным слайдам:
Задания для подготовки к ЕГЭ по математике (базовый уровень 11-20 задание) Выполнила: ученица 11 «Б» класса Болдырева Елизавета
Задание: Четыре одинаковые рубашки дешевле куртки на 8%. На сколько процентов пять таких же рубашек дороже куртки?
Решение: Стоимость четырех рубашек составляет 92% стоимости куртки. Значит, стоимость одной рубашки составляет 23% стоимости куртки. Поэтому стоимость пяти рубашек составляет 115% стоимости куртки. Это превышает стоимость куртки на 15%. Ответ: 15.
Задание: Поезд, двигаясь равномерно со скоростью 60 км/ч, проезжает мимо лесополосы, длина которой равна 400 метрам, за 1 минуту. Найдите длину поезда в метрах.
Решение: Скорость поезда равна 60 км в час, значит, за 1 минуту поезд проезжает 1 км. За это время поезд проезжает мимо лесополосы, то есть проходит расстояние, равное сумме длин лесополосы и самого поезда. Поэтому длина поезда равна 1000-400=600 метров. Ответ: 600.
Задание: Дорога между пунктами А и В состоит из подъёма и спуска, а её длина равна 8 км. Путь из А в В занял у туриста 5 часов, из которых 1 час ушёл на спуск. Найдите скорость туриста на спуске, если она больше скорости на подъёме на 3 км/ч. Ответ дайте в км/ч.
Решение: Пусть скорость, с которой турист спускался, равна х км/час, тогда его скорость на подъёме равна х − 3 км/ч, длина спуска равна х км, длина подъёма равна 4(х − 3) км. Поскольку весь путь равен 8 км, имеем: х + 4(х − 3) = 8, откуда х = 4 км/ч. Ответ: 4.
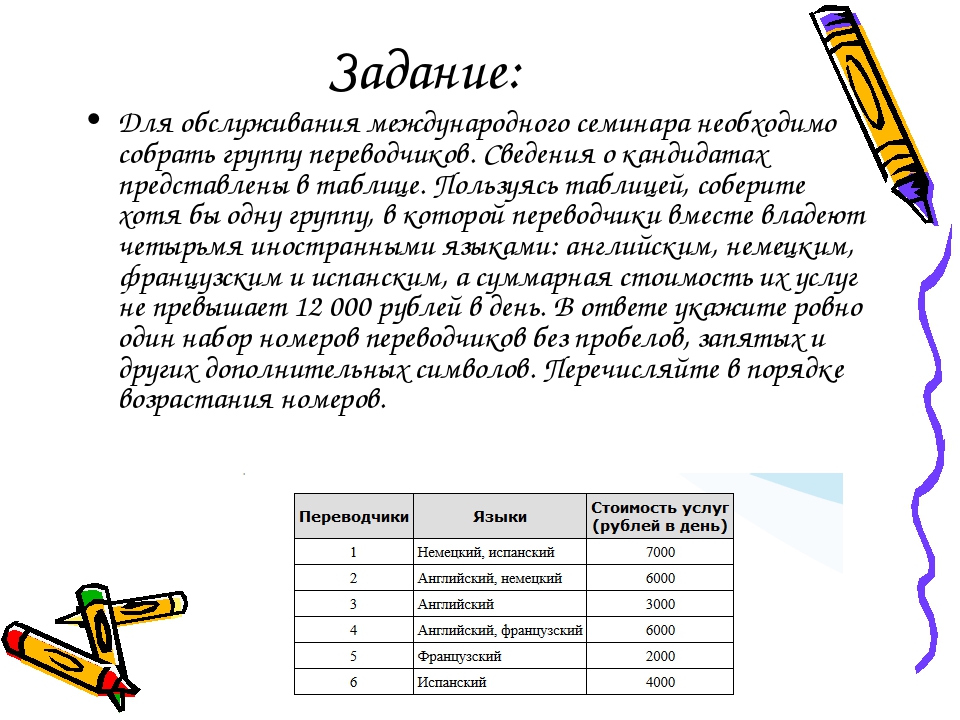
Задание: Для обслуживания международного семинара необходимо собрать группу переводчиков. Сведения о кандидатах представлены в таблице. Пользуясь таблицей, соберите хотя бы одну группу, в которой переводчики вместе владеют четырьмя иностранными языками: английским, немецким, французским и испанским, а суммарная стоимость их услуг не превышает 12 000 рублей в день. В ответе укажите ровно один набор номеров переводчиков без пробелов, запятых и других дополнительных символов. Перечисляйте в порядке возрастания номеров.
Ответ: Заметим, что стоимость услуг переводчиков, знающих только английский и французский языки меньше стоимости услуг переводчика, знающего одновременно английский и французский языки, поэтому при подборе вариантов четвёртого переводчика можно не учитывать. Переводчика, знающего только немецкий язык нет, поэтому в группу необходимо взять либо первого, либо второго переводчика. В первом случае необходимо включить в группу переводчиков, знающих английский и французский языки; дешевле выбрать переводчиков 3 и 5, тогда стоимость услуг составит 12 000 рублей в день. Остальные варианты дороже. Во втором случае необходимо включить в группу переводчиков, знающих французский и испанский языки; дешевле выбрать переводчиков 5 и 6, тогда стоимость услуг составит 12 000 рублей в день. Остальные варианты дороже. Таким образом, группа переводчиков, удовлетворяющая всем условиям, может быть собрана из переводчиков 1, 3 и 5 или из переводчиков 2, 5 и 6. Ответ: 135 или 256.
Ответ: Решение: Выберем варианты с рейтингом не ниже 4. Это магазины под номерами 1, 2, 3 и 6. Вычислим суммарную стоимость товара и доставки для оставшихся интернет-магазинов. 1-й магазин: 13 790+500 = 14290 рублей; 2-й магазин: 16 295+500 = 16795 рублей; 3-й магазин: 14 411+450 = 14861 рублей; 6-й магазин: 16 900+650 = 17 550 рублей. Выберем, исходя из полученных результатов, товар с наименьшей стоимостью. Из вычислений видно, что наименьшую цену предоставляет магазин под номером 1. Ответ: 1.
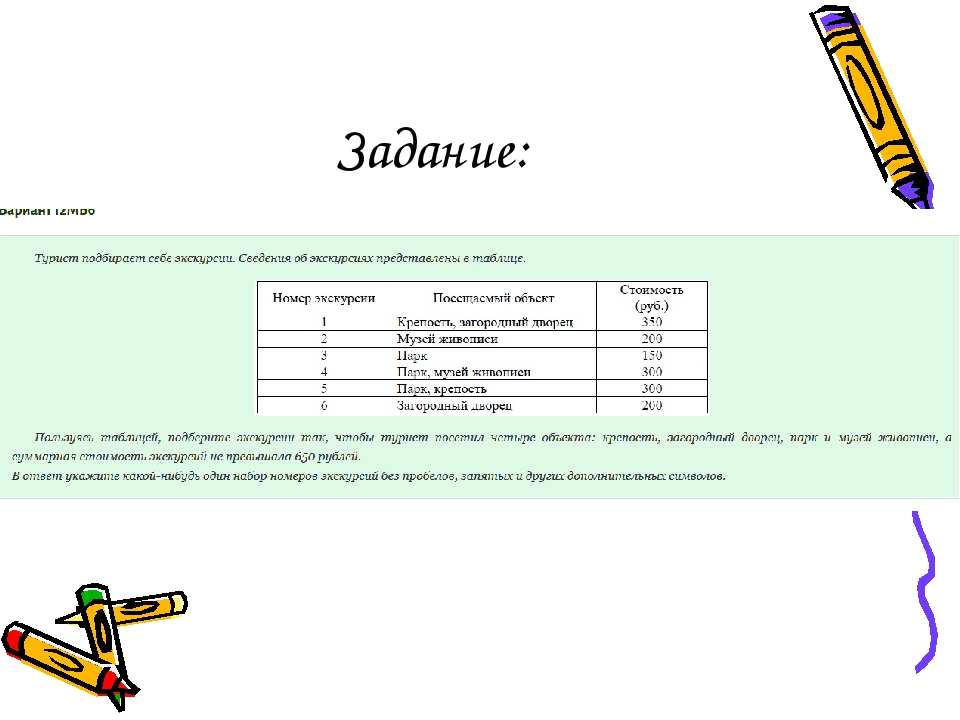
Ответ: Возьмем первую строчку — крепость и загородный дворец у нас есть и мы отдаем за них 350 рублей, нам осталось найти парк и музей живописи. Возьмем вторую и третью строчки — так мы потратим 200 и 150 рублей, а суммарно 700 рублей — это нам не подходит. Заметим четвертую строчку — нам предлагают посетить парк и музей живописи за 300 рублей. Итого с первой строчкой — 650 рублей — это нам подходит! Ответ: 14.
Задание: От деревянной правильной пятиугольной призмы отпилили все её вершины (см. рисунок). Сколько граней у получившегося многогранника (невидимые рёбра на рисунке не изображены)?
Ответ: Изначально у пятиугольной призмы 7 граней и 10 вершин. Когда от призмы отпилили все вершины количество граней стало равно 7 + 10 = 17. Ответ: 17.
Задание: Ящик, имеющий форму куба с ребром 10 см без одной грани, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.
Ответ: Площадь одной грани равна 10 · 10 = 100 см2. В кубе шесть граней, но нас просят найти только площадь пяти граней, следовательно, 100 · 5 = 500 см2. Ответ: 500.
Задание: В бак, имеющий форму правильной четырёхугольной призмы со стороной основания, равной 20 см, налита жидкость. Для того чтобы измерить объём детали сложной формы, её полностью погружают в эту жидкость. Найдите объём детали, если уровень жидкости в баке поднялся на 20 см. Ответ дайте в кубических сантиметрах.
Ответ: Объем вытесненной жидкости равен объему детали (закон Архимеда). Уровень жидкости поднялся на h=20 см, сторона основания a=20 см, значит, вытесненный объем будет равен Найденный объём является объёмом детали. Ответ: 8000.
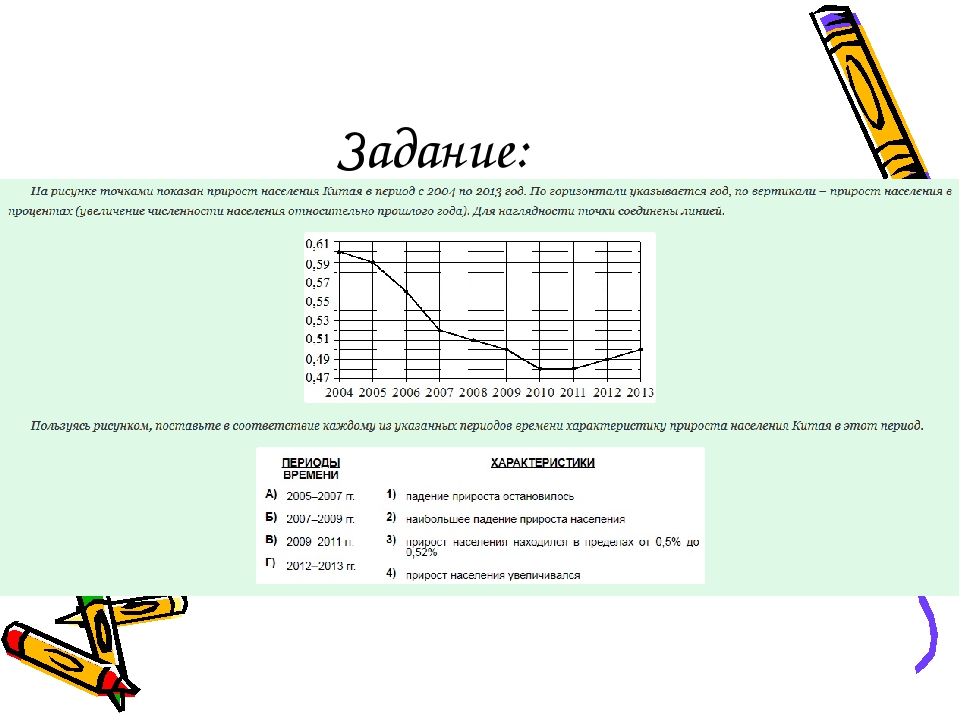
Ответ: Цена деления вертикальной шкалы составляет 0,01%. Падение прироста непрерывно продолжалось с 2004 по 2010 год. В 2010–2011 годах прирост был стабильно минимальным, и начиная с 2012 года оно начал увеличиваться. Т.е. остановка прироста произошла в 2010 году. Этот год находится в периоде 2009–2011 гг. Соответственно, имеем: В–1. Наибольшим падением прироста следует считать самую «круто» падающую линию графика на рисунке. Она приходится на период 2006–2007 гг. и составляет 0,04%, за год (0,59–0,56=0,04% в 2006 г. и 0,56–0,52=0,04% в 2007 г.). Отсюда получаем: А–2. Указанный в характеристике №3 прирост начался с 2007 года, продолжился в 2008 г. и завершился в 2009 году. Это соответствует периоду времени Б, т.е. имеем: Б–3. Прирост населения начал увеличиваться после 2011 г., т.е. в 2012–2013 гг. Поэтому получаем: Г–4.
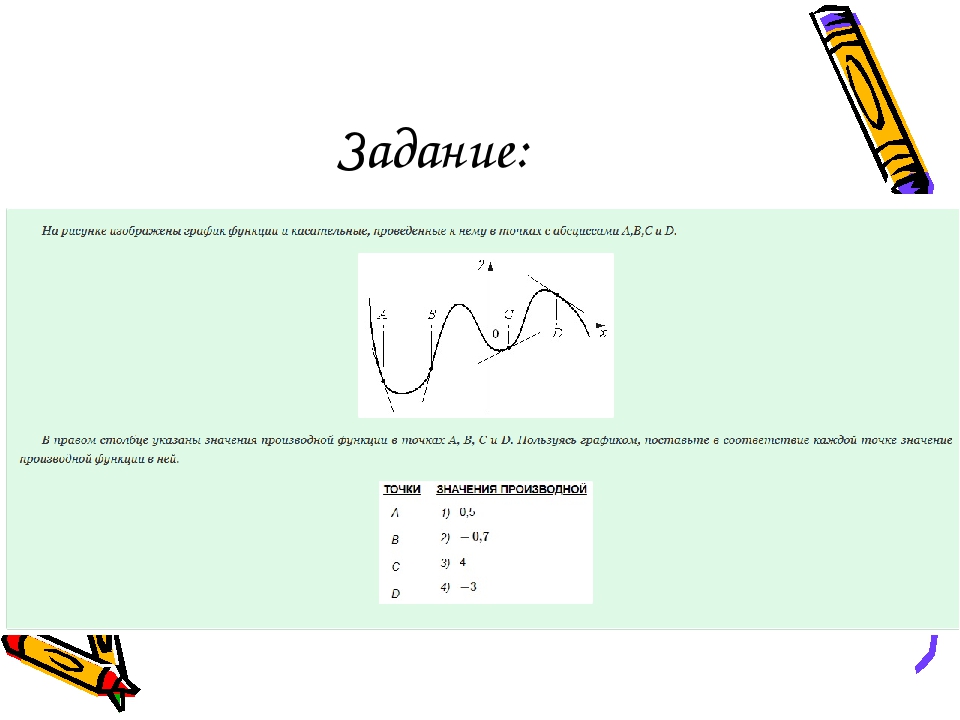
Решение: Острый угол с положит.направлением оси абсцисс образуют производные в т.В и т.С. Эти производные имеют положит.значения. Поэтому выбирать тут следует между значениями №№1 и 3. Применяя правило о том, что если угол меньше 450, то производная меньше 1, а если больше, то больше 1, делаем вывод: в т.В производная по модулю больше 1, в т.С – меньше 1. Это означает, что можно составить пары для ответа: В–3 и С–1. Производные в т.А и т.D образуют с положит.направлением оси абсцисс тупой угол. И тут применяем то же правило, немного перефразировав его: чем больше касательная в точке «прижата» к линии оси абсцисс (к отрицат. ее направлению), тем больше она по модулю. Тогда получаем: производная в т.А по модулю меньше, чем производная в т.D. Отсюда имеем пары для ответа: А–2 и D–4.
Задание: Боковая сторона равнобедренного треугольника равна 5, а основание равно 6. Найдите площадь этого треугольника.
Ответ: Площадь треугольника равна половине произведения его основания на высоту, опущенную на это основание. Высота в равнобедренном треугольнике, опущенная на основание, делит равнобедренный треугольник на два равных прямоугольных треугольника. По теореме Пифагора высота будет определяться соотношением h2 = 25 − 9 = 16, откуда h = 4. Поэтому S=1/2*6*4=12 Ответ: 12.
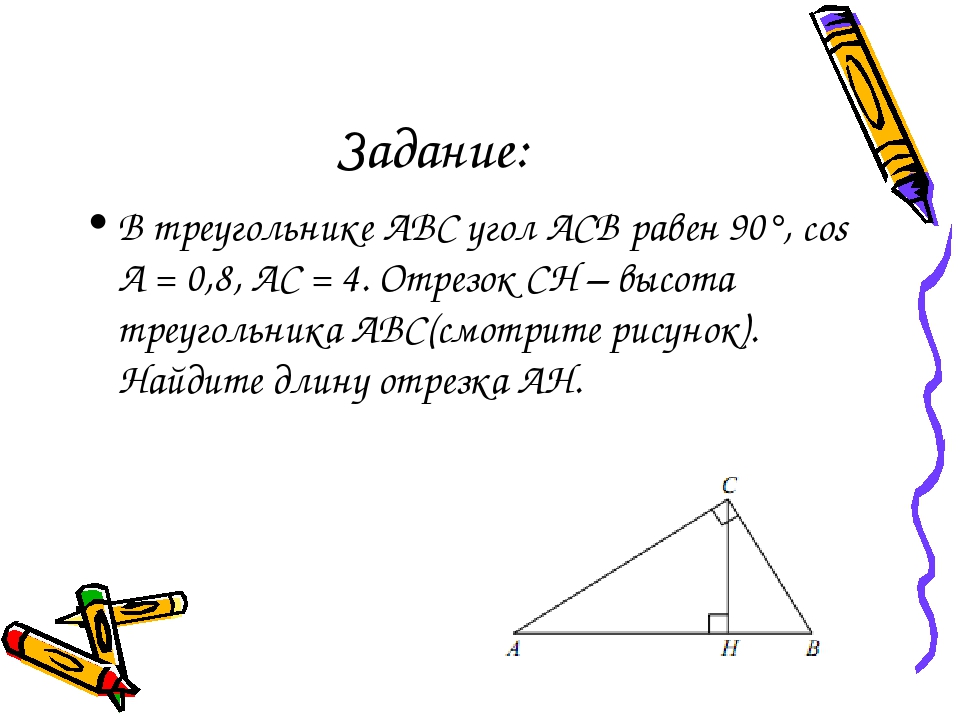
Задание: В треугольнике ABC угол ACB равен 90°, cos A = 0,8, AC = 4. Отрезок CH – высота треугольника ABC(смотрите рисунок). Найдите длину отрезка AH.
Ответ: Вспомним определение косинуса угла. Косинус – это тригонометрическая функция, которая в прямоугольном треугольнике обозначает отношение катета, прилежащего к острому углу, к гипотенузе. Запишем выражение для нахождения косинуса угла. Для этого рассмотрим треугольник ACH. Гипотенуза – это сторона прямоугольного треугольника, лежащая против угла 90°. В данном случае против угла H лежит сторона AC, то есть AC – гипотенуза. Прилежащий к углу А катет – АН. Получим cos A = АН/АС. Выразим неизвестную величину. АН = АС · cos A Вычислим. АН = АС · cos A = 4 · 0,8 = 3,2 Ответ: 3,2.
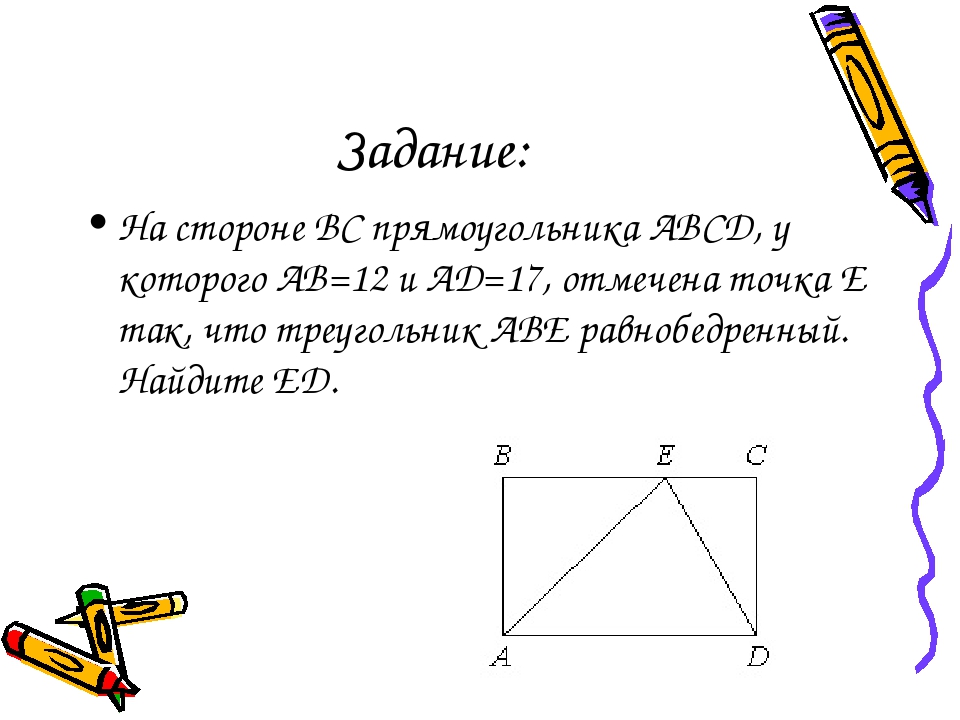
Задание: На стороне ВС прямоугольника АВСD, у которого АВ=12 и АD=17, отмечена точка Е так, что треугольник АВЕ равнобедренный. Найдите ЕD.
Решение: Т.к. по условию ∆АВЕ равнобедренный, то ВЕ=АВ=12. Т.к. АВСD прямоугольник, то ВС=АD=17, СD=АВ=12. ЕС=ВС–ВЕ=17–12=5. Рассмотрим ∆ЕСD. Т.к. АВСD прямоугольник, то угол С=900, и ∆ЕСD прямоугольный. Тогда по т.Пифагора ЕD2=ЕC2+СD2. Получаем:
Задание: В треугольной пирамиде АВСD ребра АВ, АС и АD взаимно перпендикулярны. Найдите объем этой пирамиды, если АВ=2, АС=15 и AD=11.
Ответ: Объем пирамиды: Т.к. в основании пирамиды лежит прямоугольный треугольник с катетами АВ и АС (по условию АВ перпендикулярно АС), то Sосн=АВ·АС/2. Получаем: Sосн=2·15/2=15. Т.к. AD перпендикулярно АВ и АС и пересекается с ними в одной точке, то (по признаку перпендикулярности прямой и плоскости) AD перпендикулярно плоскости основания пирамиды. Значит AD – высота пирамиды. Т.е. Н=AD=11. Отсюда имеем:
Задание: Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно √17.
Решение: Вспомним формулу площади правильной пирамиды — одна треть от произведения площади основания и высоты. Площадь основания рассчитываем по формуле площади квадрата — квадрат стороны: После этого перейдем к нахождению высоты. Для этого нам необходимо рассмотреть прямоугольный (так как основание перпендикулярно высоте) треугольник AMH. AH — половина диагонали квадрата, которая равна √2 его стороны, то есть в нашем случае диагональ равна 4√2, ну а половина — AH = 2√2. Зная гипотенузу и один из катетов, найдем высоту: После этого легко вычисляем объем: V = 1/3 • 16 •3 = 16 Ответ: 16
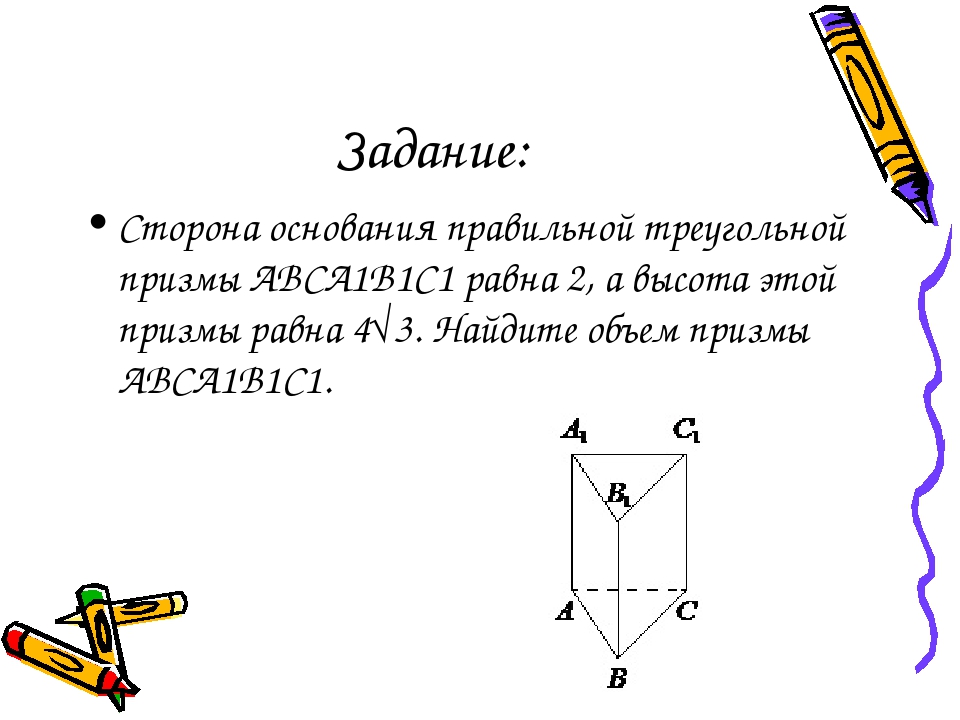
Задание: Сторона основания правильной треугольной призмы АВСА1В1С1 равна 2, а высота этой призмы равна 4√3. Найдите объем призмы АВСА1В1С1.
Ответ: Площадь правильного треугольника равна: Здесь а – сторона основания призмы. Вычислим площадь: Объем призмы: V=Sh, где h – высота призмы, S– площадь ее основания (в нашем случае – площадь правильного треугольника, лежащего в основании). Вычисляем объем: Ответ: 12
Ответ: Из рисунка видно, что число n немного меньше 0, а число m много больше отстоит от 1. Следовательно, их сумма m+n даст число в пределах [1; 2] – вариант ответа под номером 3. Число m>1, следовательно, при делении на 1 получим положительное число меньше 1. Добавляя небольшое отрицательное значение n останемся в диапазоне [0; 1]. Вариант ответа 2. Произведение mn положительного и отрицательного чисел дают отрицательное число. Подходит только один вариант [-1; 0] под номером 1. Г) Квадрат числа m много больше квадрата числа n, поэтому их разница будет положительной и принадлежать диапазону [2; 3] – вариант под номером 4. Ответ: 3214.
Ответ: Рассмотрим первое неравенство: 2x≥4 представим 4 как 22, тогда: 2x ≥ 22 x ≥ 2 Остальные неравенства решаются аналогичным образом, достаточно вспомнить, что 0,5 = ½ = 2-1: 2-x ≥ 4 2-x ≥ 22 -x ≥ 2 x≤-2 Ответ: А-4, Б-3, В-2, А-1.
Ответ: А. 2х ≥ 2 → 2х ≥ 21 → х ≥ 1. Имеем: А–1. Г. По аналогии с неравенством А получаем в ответе: х ≤ 1. Имеем: Г–2. Б. 0,5х ≥ 2 → (1/2)х ≥ 2 →2–х ≥ 21 х ≤ –1. Имеем: Б–3. В. По аналогии с неравенством Б получаем в ответе: х ≥ –1. Имеем: В–4.
Задание: В классе учится 20 человек, из них 13 человек посещают кружок истории, а 10 – кружок по математике. Выберите утверждения, которые верны при указанных условиях. 1. Каждый ученик класса посещает оба кружка. 2. Найдутся хотя бы двое из этого класса, кто посещает оба кружка. 3. Если ученик из этого класса ходит на кружок по истории, то он обязательно ходит на кружок по математике. 4. Не найдется 11 человек из этого класса, которые посещают оба кружка.
Ответ: 1. Самое очевидное верное суждение под номером 4. Не найдется 11 человек из этого класса, которые посещают оба кружка, так как кружок по математике посещают всего 10 человек, а не 11. 2. Очевидно неверное суждение под номером 1. Если бы каждый ученик класса посещал оба кружка, то каждый кружок посещали бы 20 человек. Но по условию это не так. 3. Очевидно неверное суждение под номером 3. Если бы ученик из этого класса, который ходит на кружок по истории, обязательно ходил бы на кружок по математике, то кружок по математике посещали бы 13 человек, а это противоречит условию. 4. Если ученик из этого класса ходит на кружок по истории, то он обязательно ходит на кружок по математике – верное утверждение. Всего в классе 20 человек, 10 посещают кружок по математике, остается еще 10 человек. А кружок по истории посещают 13 человек, то есть 3 точно посещают оба кружка. Ответ: 24
Задание: Кондитер испёк 40 печений, из них 10 штук он посыпал корицей, а 20 штук он собирается посыпать сахаром (кондитер может посыпать одно печенье и корицей, и сахаром, а может вообще ничем не посыпать). Выберите утверждения, которые будут выполнены при указанных условиях вне зависимости от того, какие печенья повар посыплет сахаром. 1. Найдётся 7 печений, которые ничем не посыпаны. 2. Найдётся 8 печений, посыпанных и сахаром, и корицей. 3. Если печенье посыпано корицей, то оно посыпано и сахаром. 4. Не может оказаться 12 печений, посыпанных и сахаром, и корицей.
1. Самое очевидное верное суждение под номером 1. Найдется 7 печений, которые ничем не посыпаны, так как из 40 печений 10 будут посыпаны корицей и, например, еще 20 будут посыпаны сахаром. Останется 40-10-20=10 печений, которые ничем не посыпаны. 2. Очевидно неверное суждение под номером 2. Не обязательно найдётся 8 печений, посыпанных и сахаром, и корицей, так как, кондитер может посыпать печенья, как показано в п. 1 и тогда не будет ни одного печенья посыпанного и корицей и сахаром. 3. Очевидно неверное суждение под номером 3. Не обязательно если печенье посыпано корицей, то оно посыпано и сахаром так, например, см. п. 1. 4. Не может оказаться 12 печений, посыпанных и сахаром, и корицей, так как печений посыпанных корицей всего 10. Ответ: 14
Задание: Часть сотрудников фирмы зимой ездили на курсы повышения квалификации на Кавказ. Весной было решено отправить нескольких сотрудников фирмы, не посетивших курсы на Кавказе, на стажировку в Волгоград. Выберите утверждения, которые будут выполнены при указанных условиях вне зависимости от того, кого начальство отправит на стажировку. 1. Найдётся сотрудник, который не ездил на курсы на Кавказ и не поедетна стажировку в Волгоград. 2. Среди сотрудников этой фирмы, которых не отправят на стажировку в Волгоград, есть хотя бы один, который посещал курсы на Кавказе. 3. Каждый сотрудник, который не был на курсах на Кавказе, поедет на стажировку в Волгоград. 4. Нет ни одного сотрудника этой фирмы, который посетил курсы на Кавказе и поедет на стажировку в Волгоград.
Ответ: 1. Очевидно неверное суждение под номером 1. Не всегда найдётся сотрудник, который не ездил на курсы на Кавказ и не поедет на стажировку в Волгоград, так как в Волгоград могут отправить всех оставшихся сотрудников, которые не ездили на Кавказ. 2. Самое очевидное верное суждение под номером 2. Среди сотрудников этой фирмы, которых не отправят на стажировку в Волгоград, есть хотя бы один, который посещал курсы на Кавказе, так как в Волгоград отправляют тех, кто не ездил на Кавказ, поэтому найдется хотя бы один, который посещал курсы на Кавказе. 3. Каждый сотрудник, который не был на курсах на Кавказе, поедет на стажировку в Волгоград — не верно, т.к. в Волгоград отправляют не всех оставшихся сотрудников. 4. Нет ни одного сотрудника этой фирмы, который посетил курсы на Кавказе и поедет на стажировку в Волгоград, так как те сотрудники, что ездили на Кавказ, уже не едут в Волгоград. Ответ: 24
Задание: Приведите пример трёхзначного числа, сумма цифр которого равна 20, а сумма квадратов цифр делится на 3, но не делится на 9.
Ответ: Разложим число 20 на слагаемые различными способами: 20 = 9 + 9 + 2 = 9 + 8 + 3 = 9 + 7 + 4 = 9 + 6 + 5 = 8 + 8 + 4 = 8 + 7 + 5 = 8 + 6 + 6 = 7 + 7 + 6. При разложении способами 1−4, 7 и 8 суммы квадратов чисел не кратны трём. При разложении пятым способом сумма квадратов кратна девяти. Разложение шестым способом удовлетворяет условиям задачи. Таким образом, условию задачи удовлетворяет любое число, записанное цифрами 5, 7 и 8, например, число 578.
Задание: Найдите четырёхзначное число, кратное 22, произведение цифр которого равно 24. В ответе укажите какое-нибудь одно такое число.
Ответ: Чтобы число abcd делилось на 22, оно должно делиться и на 2, и на 11. Произведение цифр 24 можно представить многими способами, основой которых являются произведения - . Признак делимости на 11: Число делится на 11, если сумма цифр, которые стоят на четных местах равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на 11. Таким образом, a+c=b+d или a+c=b+d+11 или a+c+11=b+d. Кроме того, раз число делится на 2, то оно должно быть четным. Согласно перечисленным признакам можно подобрать следующие числа: 4312, 2134, 1342, 3124
Задание: Найдите шестизначное натуральное число, которое записывается только цифрами 1 и 0 и делится на 24.
Ответ: Чтобы число делилось на 24 оно должно делится на 3 и на 8. Число делится на 8, если три его последние цифры образуют число, делящееся на 8. Искомое число записывается только нулями и единицами, значит, оно заканчивается на 000. Число делится на 3, если его сумма цифр числа делится на 3. Поскольку три последние цифры числа нули, первые три должны быть единицами. Таким образом, единственное число, удовлетворяющее условию задачи, это число 111 000. Ответ: 111 000.
Задание: На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям, получится 15 кусков, если по жёлтым — 5 кусков, а если по зелёным — 7 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?
Ответ: Если распилить палку по красным линиям, то получится 15 кусков, следовательно, линий — 14. Если распилить палку по желтым — 5 кусков, следовательно, линий — 4. Если распилить по зеленым — 7 кусков, линий — 6. Всего линий: 14 + 4 + 6 = 24 линии, следовательно, кусков будет 25.
Задание: В корзине лежит 40 грибов: рыжики и грузди. Известно, что среди любых 17 грибов имеется хотя бы один рыжик, а среди любых 25 грибов хотя бы один груздь. Сколько рыжиков в корзине?
Ответ: Груздей максимум 16 (иначе можно было бы взять 17 груздей и условие бы не выполнилось). Рыжиков максимум 24 (иначе можно было бы взять 25 груздей в нарушение условия). Известно, что в корзине всего 40 грибов. Поэтому груздей ровно 16, а рыжиков ровно 24. Ответ: 24.
Задание На поверхности глобуса фломастером проведены 12 параллелей и 22 меридиана. На сколько частей проведённые линии разделили поверхность глобуса? Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.
Решение: Двенадцать параллелей разделили глобус на 13 частей, следовательно, 13 · 22 = 286 — на столько частей разделят глобус 12 параллелей и 22 меридиана. Ответ: 286.

| Автор | |
|---|---|
| Дата добавления | 25.12.2019 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 2046 |
| Номер материала | 6510 |