
Презентация по математике на тему "Правильные многогранники"




Описание презентации по отдельным слайдам:
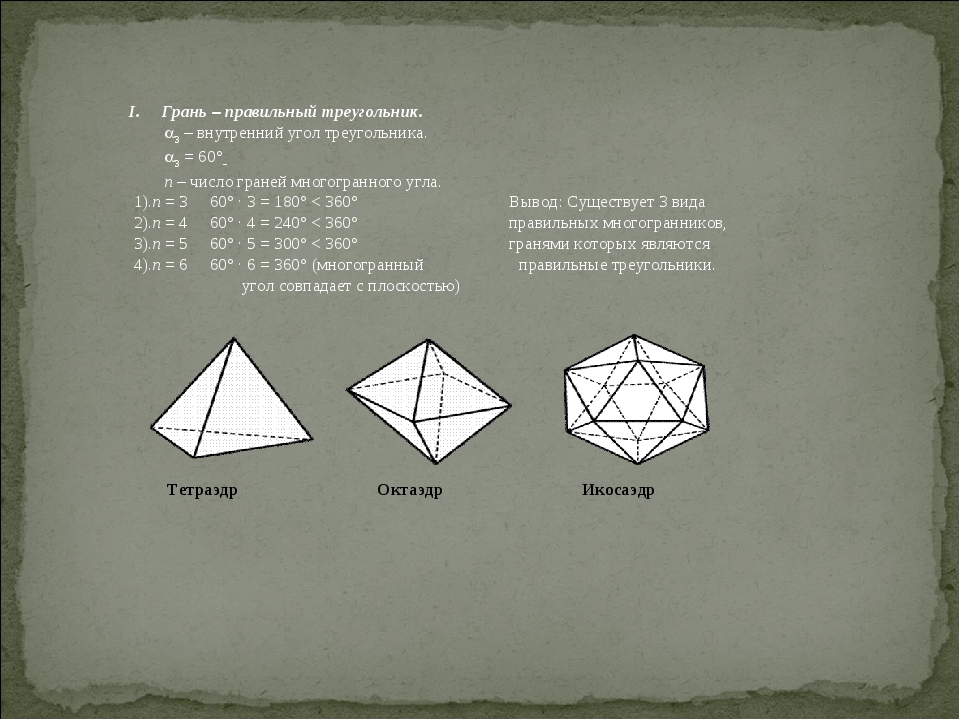
I. Грань – правильный треугольник. 3 – внутренний угол треугольника. 3 = 60° n – число граней многогранного угла. 1).n = 3 60° · 3 = 180° < 360° Вывод: Существует 3 вида 2).n = 4 60° · 4 = 240° < 360° правильных многогранников, 3).n = 5 60° · 5 = 300° < 360° гранями которых являются 4).n = 6 60° · 6 = 360° (многогранный правильные треугольники. угол совпадает с плоскостью) Тетраэдр Октаэдр Икосаэдр
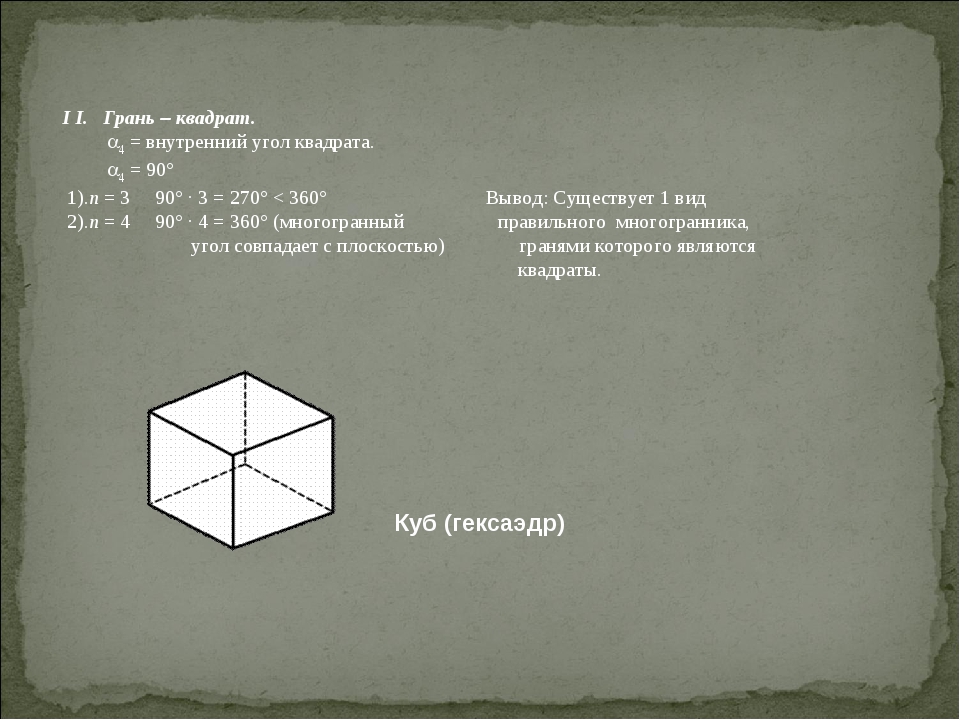
I I. Грань – квадрат. 4 = внутренний угол квадрата. 4 = 90° 1).n = 3 90° · 3 = 270° < 360° Вывод: Существует 1 вид 2).n = 4 90° · 4 = 360° (многогранный правильного многогранника, угол совпадает с плоскостью) гранями которого являются квадраты. Куб (гексаэдр)
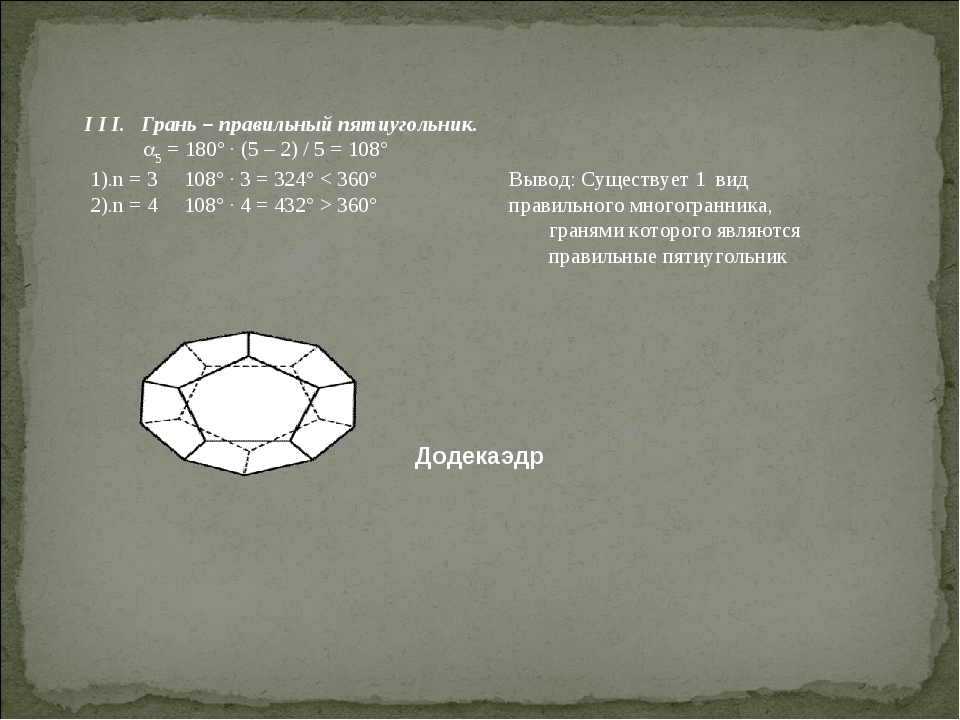
I I I. Грань – правильный пятиугольник. 5 = 180° · (5 – 2) / 5 = 108° 1).n = 3 108° · 3 = 324° < 360° Вывод: Существует 1 вид 2).n = 4 108° · 4 = 432° > 360° правильного многогранника, гранями которого являются правильные пятиугольник Додекаэдр
I V. Грань – правильный шестиугольник. 6 = 120° Вывод: правильный многогранник 1).n = 3 120° · 3 = 360° (многогранный гранями которого являются гол совпадает с плоскостью) правильные шестиугольники не существует. Вывод: существует 5 видов правильных многогранников. Почему правильные многогранники получили такие имена? Это связано с числом их граней. В переводе с греческого языка: эдрон – грань окто - восемь тетра - четыре додека - двенадцать гекса - шесть икоси - двадцать
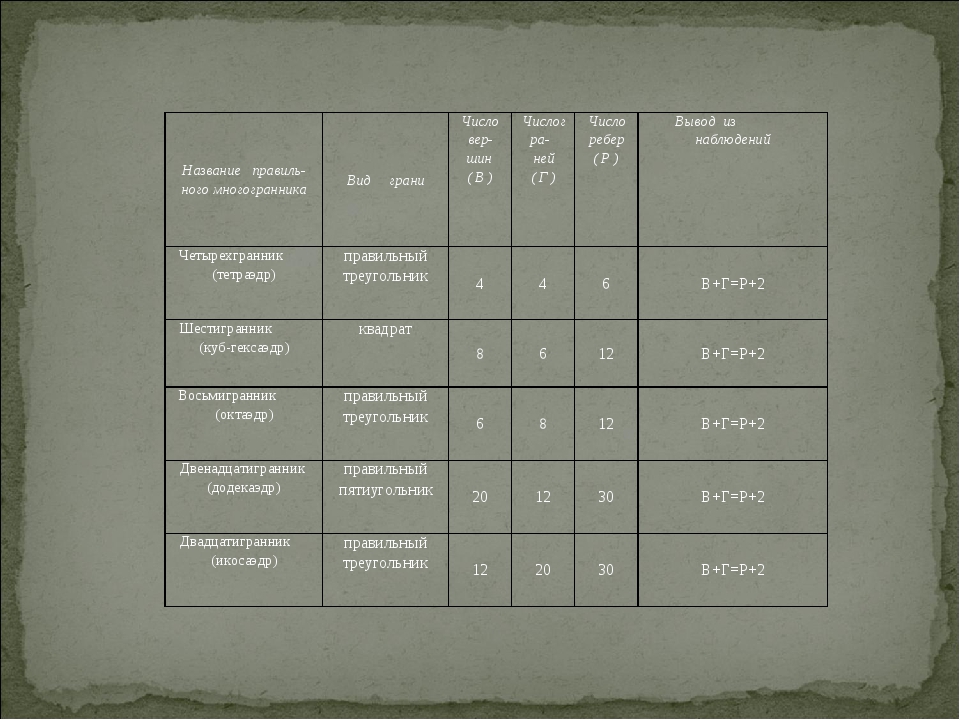
Название правиль-ного многогранника Вид грани Число вер-шин ( В ) Числогра- ней ( Г ) Число ребер ( Р ) Вывод из наблюдений Четырехгранник (тетраэдр) правильный треугольник 4 4 6 В+Г=Р+2 Шестигранник (куб-гексаэдр) квадрат 8 6 12 В+Г=Р+2 Восьмигранник (октаэдр) правильный треугольник 6 8 12 В+Г=Р+2 Двенадцатигранник (додекаэдр) правильный пятиугольник 20 12 30 В+Г=Р+2 Двадцатигранник (икосаэдр) правильный треугольник 12 20 30 В+Г=Р+2

| Автор | |
|---|---|
| Дата добавления | 20.10.2019 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 1214 |
| Номер материала | 6363 |