Презентация по математике на тему "Решение неравенств методом интервалов"

Решение иррациональных неравенств методом интервалов

«Если бы люди знали, как много я тружусь, чтобы добиться мастерства, они перестали бы считать меня таким уж талантливым» Микеланджело

Цель урока: Усвоить алгоритм решения иррациональных неравенств методом интервалов. Научиться решать иррациональные неравенства с применением алгоритма.

Иррациональными называют неравенства, в которых переменные входят под знак корня

Решим неравенства: 1. 2. 3.

Решение первого неравенства 1. равносильно Шаг 1. Рассмотрим иррациональную функцию и найдем область определения - область определения Шаг 2. Вычислим нули функции - нуль функции Шаг 3. Ответ

2. равносильно Шаг 1. Рассмотрим иррациональную функцию и найдем область ее определения - область определения Шаг 2. Вычислим нули функции - нуль функции Шаг 3. Ответ

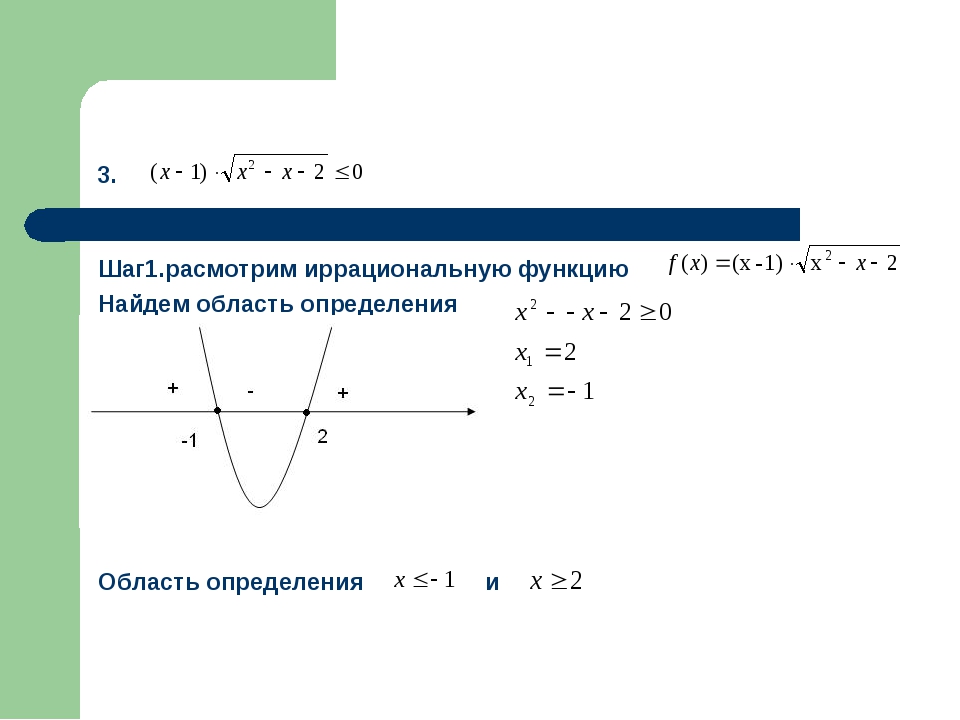
3. Шаг1.расмотрим иррациональную функцию Найдем область определения Область определения и

Шаг 2. Вычислим нули функции -1; 1; 2 - нули функции Шаг 3. Ответ: и

Алгоритм решения иррациональных неравенств: Введение иррациональной функции; нахождение области определения функции. Вычисление нулей функции. На координатной прямой: отмечаем нули функции, принадлежащие области определения; определяем знак функции на каждом промежутке; с учетом знака неравенства выписываем ответ.

Упражнения для самостоятельного решения: : 1. 2. 3. Для контроля используем лист самопроверки

Проверяем: Неравенство 1 шаг 2 шаг 3 шаг Неравенство 1 шаг и 2 шаг 3 шаг Неравенство 1 шаг 2 шаг и 3 шаг

Оценка: 5 баллов – задание выполнено полностью и верно. 4 балла – задание верно выполнено на первом и втором шаге. Допущена ошибка в вычислениях на третьем шаге. 3 балла - задание верно выполнено на первом шаге, вычислительная ошибка на втором шаге. В остальных случаях – 2 балла.

Домашняя работа обязательная: 1. 2. 3. ответ ответ ответ