
Презентация "Построение циркулем и линейкой"

Краткое описание документа:
В данном уроке речь пойдёт об основных способах построения различных фигур при помощи подручных инструментов: циркуль и линейка. Любое построение удобнее всего осуществлять именно с этими чертёжными помощниками. Циркулем можно проводить любые окружности. Что значит любые? Это значит, что можно выбрать любой центр, а также можно выбрать любой радиус окружности. С помощью линейки можно проводить любые линии, соединять точки, получать новые точки и так далее. Итак, мы имеем два чертёжных инструментов, которые используем для более-менее сложных задач на построение.

слайды 1-2 (Тема презентации "Построение циркулем и линейкой", пример)
Есть раздел геометрии, который именно этим занимается: евклидова геометрия. Евклидова геометрия является такой теорией, которая зависит от аксиом, выведенных ещё в античное время (в период третьего века до нашей эры). Сам математик составил ряд утверждений, часть которых была доказана в девятнадцатом веке, а другая часть – опровергнута.
Так вот Евклид говорил о возможности построить прямую линию от любой точки к другой. Во-вторых, он предлагал продолжать прямую от ограниченной. В-третьих, он утверждал возможность описания круга из любого центра. В-четвёртых, он утверждал равенство прямых углов. Напоследок, он говорил об образовании внутренних односторонних углов при пересечении одной прямой двух других. Более того, он говорил о том, что они вновь встретятся.
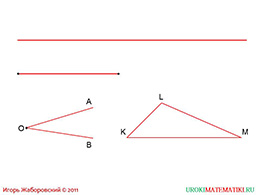
Представим, что у нас есть некоторая прямая, некоторый отрезок, некоторый угол «АОВ» и некоторый треугольник «KLM». Можем ли мы все эти элементы построить «от руки» или «на глаз»? Предложите одному из учащихся продемонстрировать это на доске, а потом проверьте результат с помощью линейки. Определите, насколько велика погрешность во всех случаях. Объясните, что математика, в нашем случае её раздел – геометрия, является точной наукой, поэтому ошибочные данные её не интересуют.

слайды 3-4 (примеры)
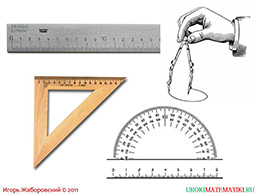
Какие подручные инструменты мы можем использовать, чтобы избежать погрешности при построении прямых, отрезков, углов и треугольников? Этими инструментами являются простая линейка, циркуль, линейка в форме треугольника, а также транспортир. Оба вида линейки помогут измерить отрезок и провести точную линию. Циркуль поможет работать с окружностями и находить точки пересечения, а транспортир поможет измерить необходимый угол.
Такой уникальный инструмент как транспортир делается из различных материалов: металл, дерево, пластик. Известно, что идентичный инструмент придумали и использовали ещё в Вавилоне. Сам Ломоносов отдавал должное данному инструменту при исследовании фундаментальных наук. Стоит показать транспортиры различного размера и спросить у учащихся, что они замечают, в чём их различие. В итоге объяснить, что размер инструмента прямо пропорционален его точности.
Теперь стоит подробнее остановиться на инструменте, который мы используем для того, чтобы начертить окружность и дугу. Состоящий изначально из металла циркуль содержит две части и соединяется шарниром. Особенность инструмента в том, что одна часть представляет собой иглу и помогает фиксировать циркуль в нужной точке. Вторая же часть пишущая и позволяет на необходимом расстоянии создать дугу. Наконечник второй части – обычно грифель, однако может содержать держатель, где будет фиксироваться карандаш. Оба варианта возможны, просто сравните ваш циркуль с циркулем соседа. Очень часто для черчения или навигации циркуль могут использовать только в измерительных целях. В таких случаях оба наконечника будут являться иглами. Например, это работа с топографической картой или же при перенесении данных с карты на бумагу. Футляр для циркуля называется готовальней. У кого из присутствующих он есть?


слайды 5-6 (примеры)
Что значит, построить точку с помощью циркуля и линейки? Изначально берётся база построения или некоторое количество точек (обычно, это точка нуль и точка один). Если повторять следующие действия, то можем получить ряд других точек. Поэтому стоит помнить, что:
- Через две точки мы всегда можем провести одну прямую (можно и через большее количество, но тогда они должны находиться на одной прямой);
- Используя эти же две точки можно провести одну окружность (никак ни при большем количестве);
- При пересечении прямых получим одну точку стыка, а при пересечении двух окружностей – две точки пересечения.
Инструмент, который поможет нам построить прямую через две точки – линейка. Работать с окружностями мы будем, используя циркуль. Теперь необходимо перейти к практической части и понять процесс построения фигуры. Поэтому перечислим этапы, из которых состоит задача по построению фигуры или других геометрических элементов.
Решение состоит из четырёх частей. Первая часть – анализ. Здесь имеется в виду анализ исходных данных и составление плана решения. После того, как план решения составлен, закончился первый этап задачи на построение. Осуществляется второй этап – собственно построение. Построение ведётся по уже намеченному плану. Третий этап – доказательство. Вот построили мы фигуру и нам необходимо доказать то, что построенная фигура удовлетворяет всем условиям задачи. Наконец, четвёртый этап – это исследование задачи. Вот мы видим нужную фигуру. Вопрос: а при любых ли значениях исходных возможно это построение? Одна ли только фигура удовлетворяет этим данным? Итак, есть четыре этапа, которые необходимо проиллюстрировать на примере, но изначально, ответим на вопрос: какого рода задачи можно решать при помощи перечисленных инструментов и используя данные этапы? Всё то, что связано с углами (построить, имея равный), прямыми (параллельные, перпендикулярные и т.д.), а также отрезками (проведение, пересечение, деление).
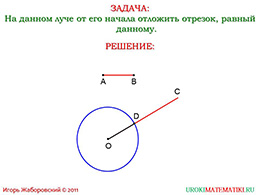
слайд 7 (пример)
Теперь необходимо применить полученные теоретические знания на практике. Посмотрим на наш пример, где дан луч, от начала которого необходимо отложить отрезок. Полученный отрезок должен быть равен изначальному отрезку «АВ». Задача вполне ясна! Возможно, кто-то предложить просто-напросто взять линейку, измерить отрезок и провести такой же отрезок, так же используя линейку. Идея прекрасная, но необходимо построить отрезок, не зная параметров изначального, ведь в изначальном условии это неизвестно. Поэтому имеем некоторый отрезок с абсолютно любой длинной и необходимо проиллюстрировать идентичного размера отрезок на луче. Всё это должно происходит в одной плоскости.
В данном случае лучшим инструментом будет циркуль, который поможет измерить расстояние «АВ» и круговым движением показать, где этот отрезок может находиться на некотором луче (длину точную не знаем, но известно, что луч имеет одну точку и идёт в бесконечность).
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6317 |
| Номер материала | 247 |