
Урок "Третий признак равенства треугольников"

Краткое описание документа:
Видеоурок «Третий признак равенства треугольников» содержит доказательство теоремы, представляющей собой признак равенства двух треугольников по трем сторонам. Данная теорема является важной частью геометрии. Она часто используется для решения практических задач. Ее доказательство базируется на известных уже ученикам признаках равенства треугольников.
Доказательство данной теоремы сложое, поэтому для улучшения качества обучения, формирования умения доказывать геометрические утверждения желательно использовать данное наглядное пособие, которое поможет сконцентрировать внимание учеников на изучаемом материале. Также оно при помощи анимации, наглядной демонстрации построений и доказательства дает возможность улучшить качество обучения.
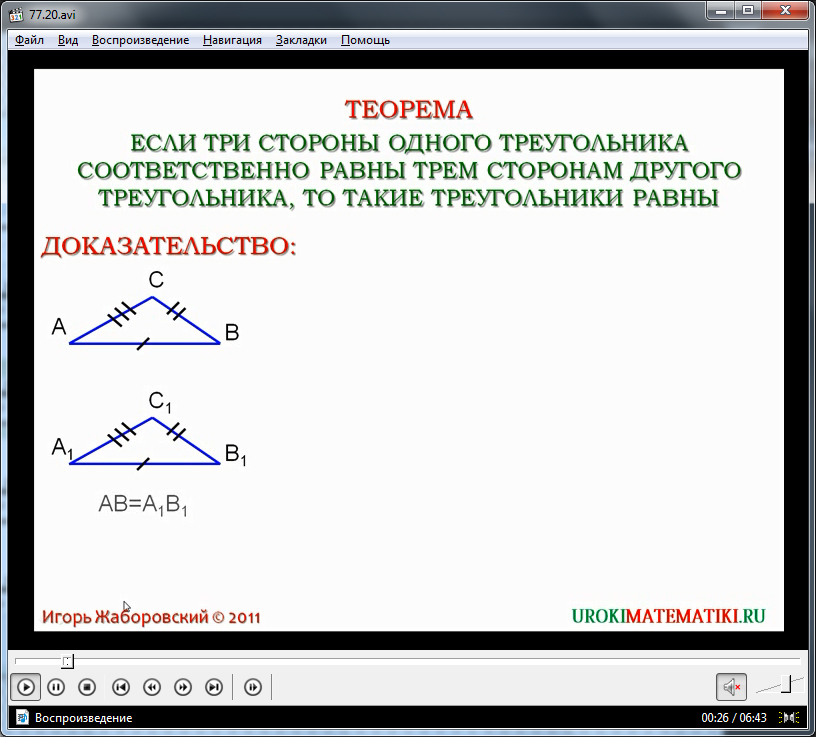
В начале урока демонстрируется название темы и формулируется теорема о том, что треугольники равны в случае, если все стороны одного треугольника попарно равны всем сторонам второго треугольника. Текст теоремы демонстрируется на экране и может быть записан учениками в тетрадь. Далее рассматривается доказательство данной теоремы.
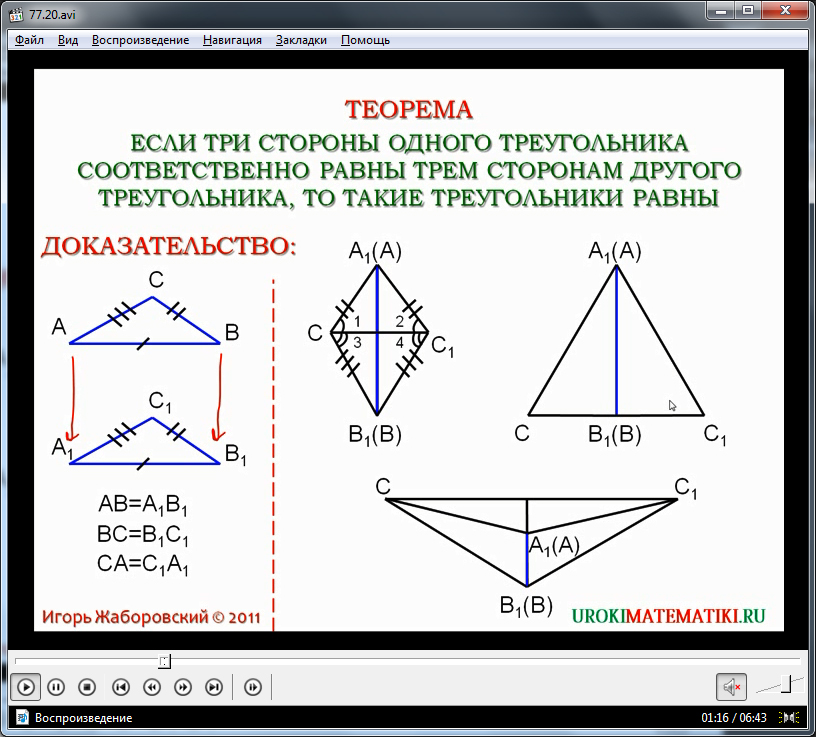
Для доказательства теоремы строятся треугольники ΔАВС и ΔА1В1С1. Из условия теоремы следует, что стороны попарно равны, то есть АВ=А1В1, ВС=В1С1 и АС=А1С1. В начале доказательства демонстрируется наложение треугольника ΔАВС на ΔА1В1С1 так, чтобы вершины А и А1, а также В и В1 данных треугольников совместились. При этом вершины С и С1 должны располагаться по разные стороны от наложенных сторон АВ и А1В1. При данном построении возможно несколько вариантов расположения элементов треугольников:
- Луч С1С лежит внутри угла ∠А1С1В1.
- Луч С1С совпадает с одной из сторон угла ∠А1С1В1.
- Луч С1С лежит вне угла ∠А1С1В1.
Каждый случай необходимо рассматривать отдельно, так как доказательство не может быть одинаковым для всех данных случаев. В первом случае рассматривается два треугольника, образованных в результате построения. Так как по условию в данных треугольниках стороны АС=А1С1, а ВС=В1С1, то получившиеся треугольники ΔВ1С1С и ΔА1С1Сравнобедренные. Используя изученное свойство равнобедренных треугольников, мы можем утверждать, что углы ∠1 и ∠2 равны между собой, а также ∠3 и ∠4 равны. Так как данные углы равны, то и в сумме ∠1 и ∠3, а также ∠2 и ∠4 также будут давать равные углы. Поэтому углы ∠С и ∠С1 равны. Доказав данный факт, мы можем заново рассмотреть треугольники ΔАВС и ΔА1В1С1, в которых стороны ВС=В1С1 и АС=А1С1 по условию теоремы, и доказано, что углы между ними ∠С и ∠С1 также равны. Соответственно, данные треугольники будут равны по первому признаку равенства треугольников, который уже известен ученикам.
Во втором случае при наложении треугольников точки С и С1 легли на одну прямую, проходящую через точку В(В1). В сумме двух треугольников ΔАВС и ΔА1В1С1 получился треугольник ΔСАС1, в котором две стороны АС=А1С1 по условию теоремы являются равными. Соответственно, данный треугольник является равнобедренным. В равнобедренном треугольнике при равных сторонах лежат равные углы, поэтому можно утверждать, что углы ∠С=∠С1. Также из условия теоремы следует, что стороны ВС и В1С1 равны между собой, поэтому ΔАВС и ΔА1В1С1 с учетом изложенных фактов равны между собой по первому признаку равенства треугольников.
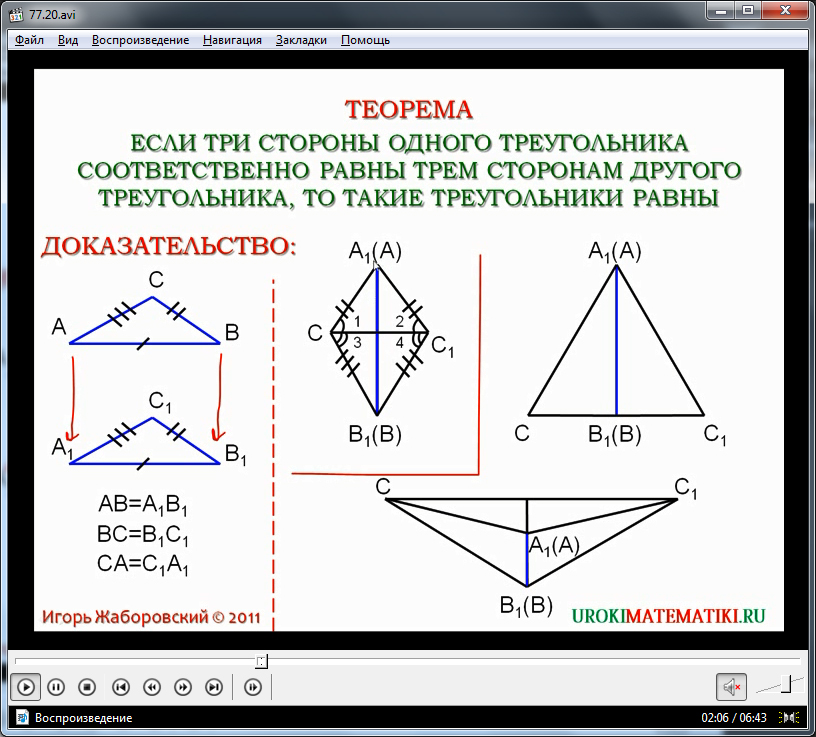
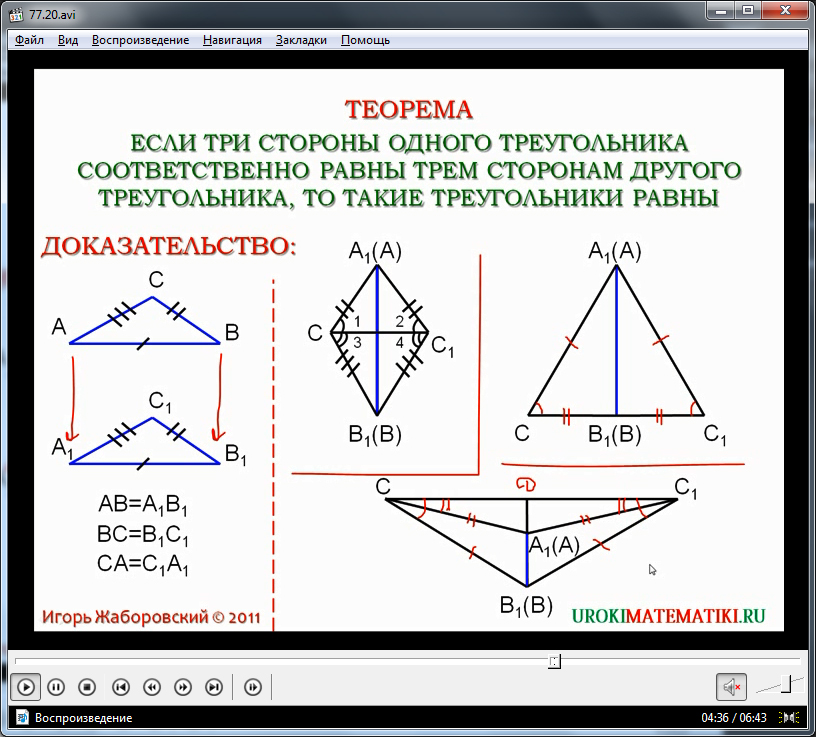
Доказательство в третьем случае, аналогично первым двум, использует первый признак равенства треугольников. Построенная наложением треугольников геометрическая фигура при соединении отрезком вершин С и С1 преобразуется в треугольник ΔВ1С1С. Данный треугольник является равнобедренным, так как его стороны В1С1 и В1С по условию равны. А при равных сторонах в равнобедренном треугольнике углы ∠С и ∠С1 также равны. Так как по условию теоремы равны стороны АС=А1С1, то углы при них в равнобедренном треугольнике ΔАСС1 также равны. С учетом того, что углы ∠С и ∠С1 равны, и углы ∠DCAи ∠DC1A равны между собой, то и углы ∠АСВ и ∠АС1В также равны. Учитывая данный факт, для доказательства равенства треугольников ΔАВС и ΔА1В1С1 можно использовать первый признак равенства треугольников, так как две стороны у данных треугольников равны по условия, а равенство углов между ними доказано в ходе рассуждений.
В конце видеоурока демонстрируется важное приложение третьего признака равенства треугольников – жесткость данной геометрической фигуры. На примере разъясняется, что значит данное утверждение. В качестве примера гибкой конструкции приводятся две рейки, соединенные гвоздем. Данные рейки могут быть раздвинуты и сдвинуты под любым углом. Если же к рейкам прикрепить еще одну, соединенную концами с имеющимися рейками, то мы получим жесткую конструкцию, в которой невозможно поменять угол между рейками. Получение треугольника с данными сторонами и другими углами невозможно. Это следствие теоремы имеет важное практическое значение. На экране изображаются инженерные конструкции, в которых применяется данное свойство треугольников.
Видеоурок «Третий признак равенства треугольников» облегчает учителю подачу нового материала на уроке геометрии по данной теме. Также видеоурок может с успехом использоваться для дистанционного обучения математике, поможет разобраться в сложностях доказательства ученикам самостоятельно.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 9332 |
| Номер материала | 507 |