
Урок "Свойства равнобедренного треугольника"

Краткое описание документа:
Видеоурок «Свойства равнобедренного треугольника» раскрывает понятие равнобедренного треугольника и его составляющих, описывает доказательства важных свойств равнобедренного треугольника. Задача данного видеоурока – сделать изучение данной темы интересным, а материал – легко запоминающимся. Это наглядное пособие, которое концентрирует внимание ученика на изучении новой темы и освобождает учителя для улучшения качества индивидуальной работы.
При помощи анимационных эффектов приведенные доказательства представляются в легко усваиваемой форме, понятны и хорошо запоминаются. Видеоурок полностью раскрывает тему, вполне заменяя учителя в части урока, которая требует объяснения нового материала.
Видеоурок начинается с объявления названия темы. В начале урока дается определение равнобедренного треугольника как треугольника, две стороны которого равны. Определение выведено на экран и выделено цветом для лучшего его запоминания. На рисунке, сопровождающем определение, изображен треугольник ΔАВС, две стороны которого равны АВ=ВС. Далее треугольник разбивается на элементы – две боковые стороны и основание. Названия сторон выделены красным цветом для лучшего запоминания. В данном треугольнике имеются боковые стороны АВ и ВС, которые равны между собой, поэтому треугольник наывается равнобедренным, а третья сторона АС называется основанием треугольника.
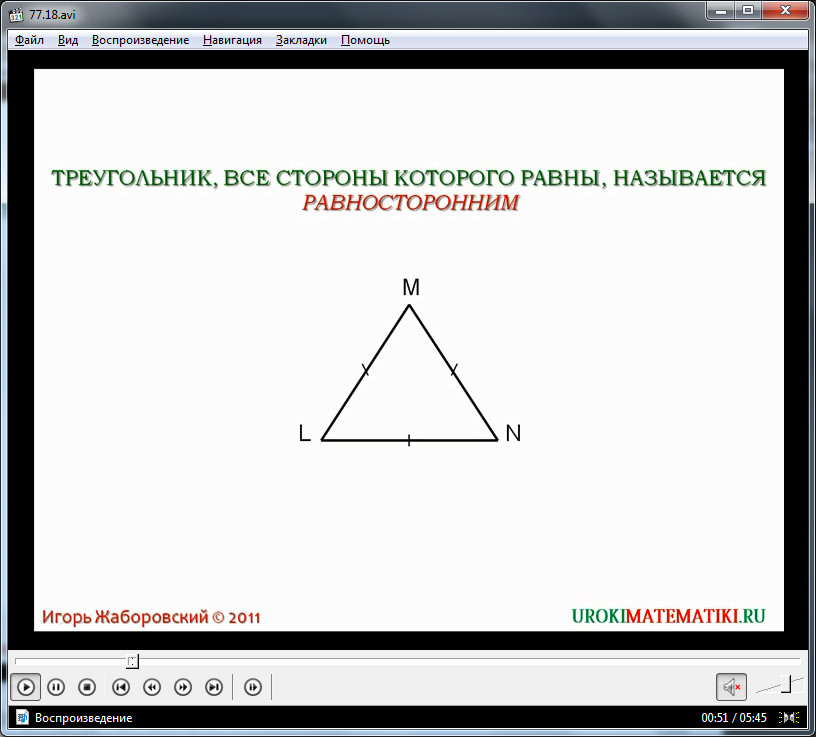
Вторым разбирается понятие равностороннего треугольника. Определение равностороннего треугольника как треугольника, все стороны которого равны, выведено на экран и выделено цветом для лучшего запоминания текста. В изображенном ниже определения треугольнике ΔLMN стороны LM, LN, MN равны между собой. Поэтому данный треугольник является равносторонним.
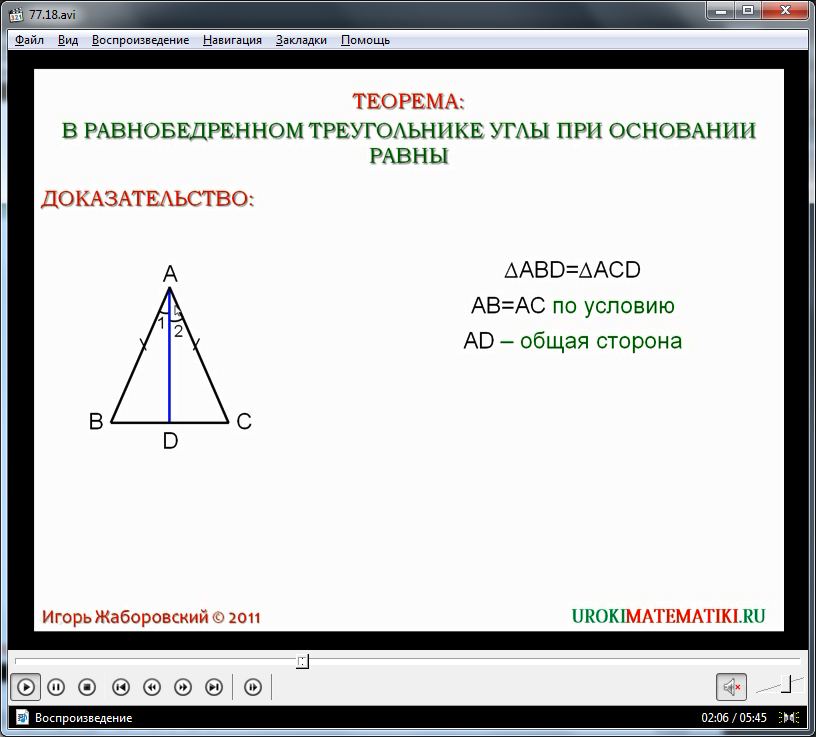
Далее разбирается доказательство теоремы о том, что в равнобедренном треугольнике расположенные при основании углы равны. Для доказательства данного утверждения изображается равнобедренный треугольник ΔАВС. В данном треугольнике стороны АВ и АС равны. ВС является основанием треугольника. Необходимо доказать, что в данном треугольнике угол ∠В равен углу ∠С. Для доказательства в данном треугольнике строится биссектриса угла ∠А - АD. Биссектриса делит угол ∠А пополам, образуя равные углы ∠1 и ∠2. Равенство треугольников ΔАВD и ΔАСD равны по первому признаку равенства треугольников. Действительно, по условия стороны АВ=АС, сторона ADявляется общей стороной двух треугольников, а углы ∠1=2, так как АD – биссектриса. Данные факты являются достаточным набором свойств данных треугольников для утверждения, что они между собой равны по первому признаку равенства треугольников. Далее пользуемся уже известным ученикам утверждением, что напротив равных сторон в равных треугольниках располагаются равные углы. Поэтому отмечается, что в данны треугольниках напротив стороны AD в первом треугольнике лежит угол ∠В, а во втором треугольнике напротив нее – угол ∠С. И эти углы равны между собой. Данная теорема полностью доказана.
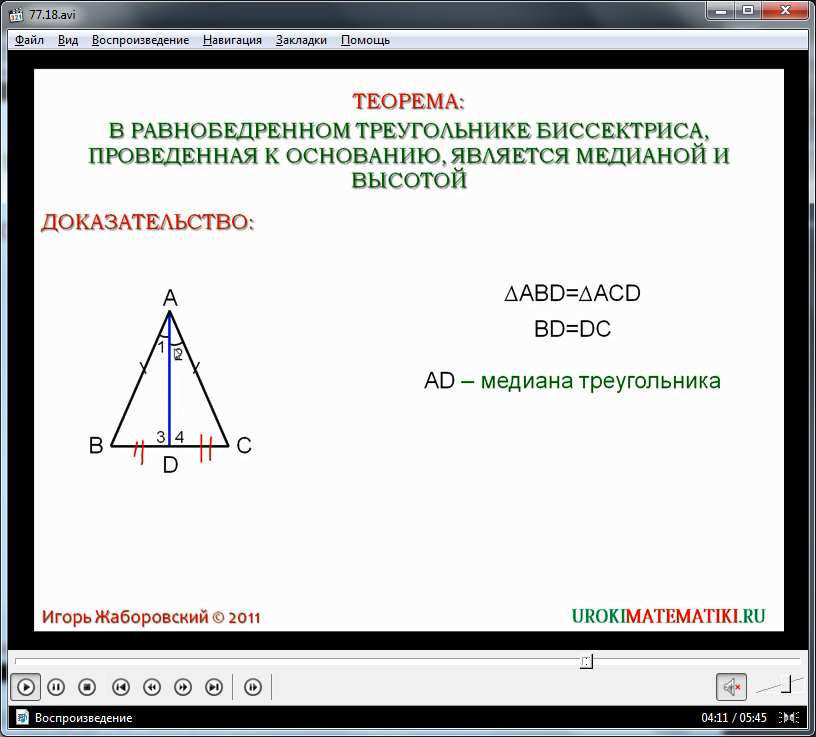
В следующей части видеоурока рассматривается теорема о том, что биссектриса, направленная к основанию треугольника, это и медиана, и высота данного треугольника. Для доказательства данной теоремы на экран выведен треугольник, построенный при доказательстве первой теоремы. Мы уже доказали, что его биссектриса делит на два равных треугольника ΔАВD и ΔАСD. Из этого равенства следует, что стороны BDи DC также будут между собой равны. Соответственно, отрезок ADпроведен к середине стороны ВС. А это значит, что AD является медианой треугольника ΔАВС, проведенной из вершины А. Первая часть теоремы – о том, что биссектриса, направленная к основанию - это медиана равнобедренного треугольника, доказана.
Также из равенства треугольников ΔАВD=ΔАСD следует, что и углы ∠3 и ∠4 равны между собой. При этом они являются смежными углами, а как известно, сумма смежных углов равна 180°. Следовательно, их градусная мера будет равна 90°, то есть углы ∠3 и ∠4 – прямые. Мы видим, что отрезок AD, опущенный из вершины А на сторону ВС является перпендикуляром к прямой, содержащей ВС – соответственно, этот отрезок является и высотой данного треугольника. Данная теорема доказана.
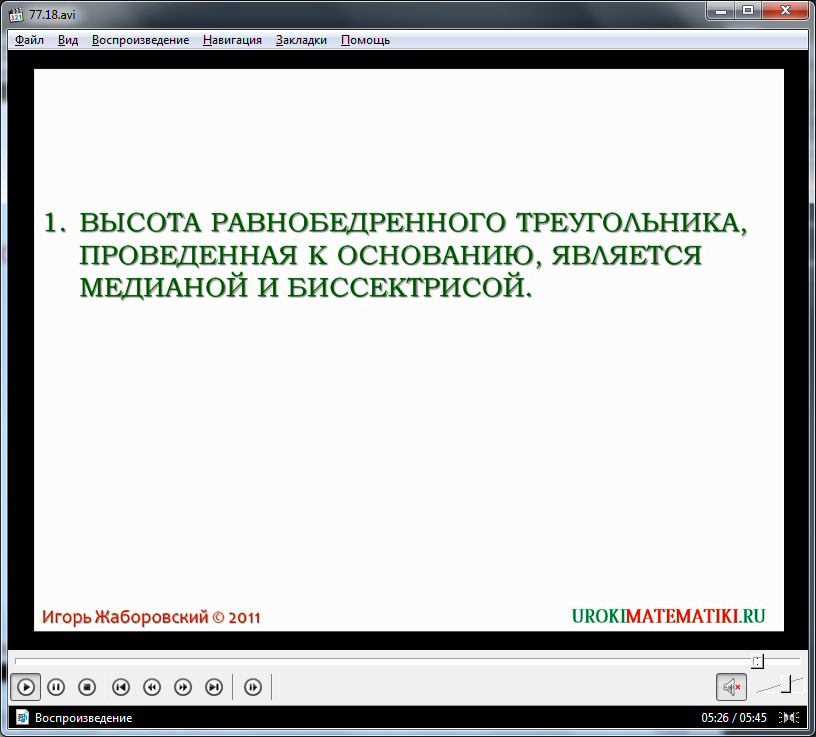
Следствием из доказанной теоремы будет утверждение о том, что медиана, проведенная к основанию равнобедренного треугольника, является биссектрисой и высотой треугольника. Также справедливым будет следствие, что высота, проведенная к основанию треугольника, является также биссектрисой и медианой. Следствия выведены на экран для лучшего запоминания. Также они могут быть предложены ученикам на запись в тетрадь.
Видеоурок «Свойства равнобедренного треугольника» может быть использован в качестве наглядного пособия на обычном уроке в школе во время изучения данной темы. Также видеурок может помочь освоить материал ученикам при самостоятельном изучении геометрии. Наглядное доказательство теорем при помощи данного пособия станет незаменимым и при дистанционном обучении.
| Автор | |
|---|---|
| Дата добавления | 02.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 6497 |
| Номер материала | 505 |