
Презентация "Правильная пирамида"

Краткое описание документа:
Презентация «Правильная пирамида» представляет учебный материал по данной теме в наглядном виде. В большинстве задач, в которых решается пирамида, имеется в виду правильная пирамида. С помощью данной презентации учитель может сформировать умение учеников решать задачи, в которых необходимо знать свойства правильной пирамиды. В ходе презентации ученикам представляются свойства правильной пирамиды, демонстрируется решение задач по данной теме.
Особенностью наглядного материала для раздела геометрии является необходимость представить на плоскости изображения объемных тел, свойства которых рассматриваются, в которых нужно выполнять построения для решения задач. В презентации данные построения легче продемонстрировать, так как средствами компьютерной техники могут быть сделаны четкие понятные построения, а с помощью анимационных средств они перестраиваются, преобразуются. Способствует пониманию материала и лучшему его запоминанию и возможность выделения текста и деталей рисунка разными цветами.
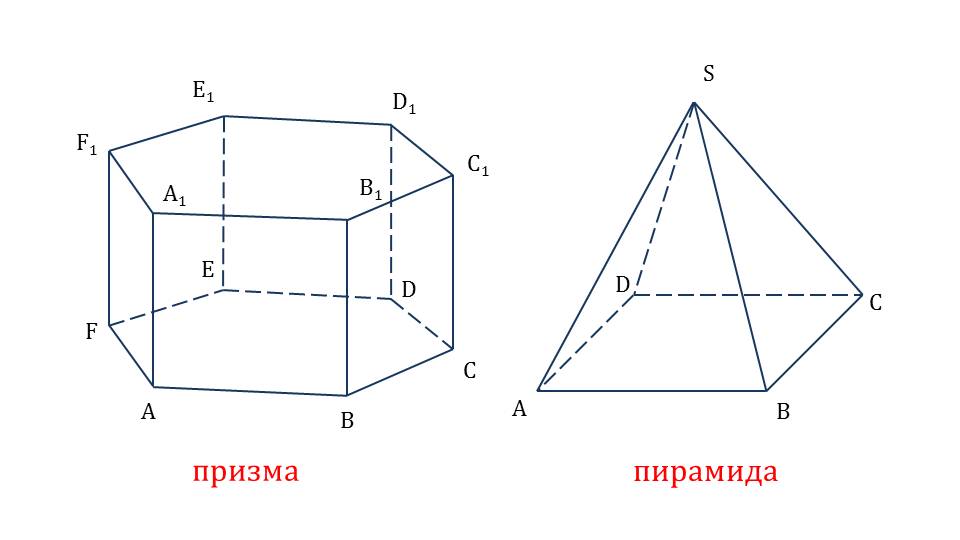
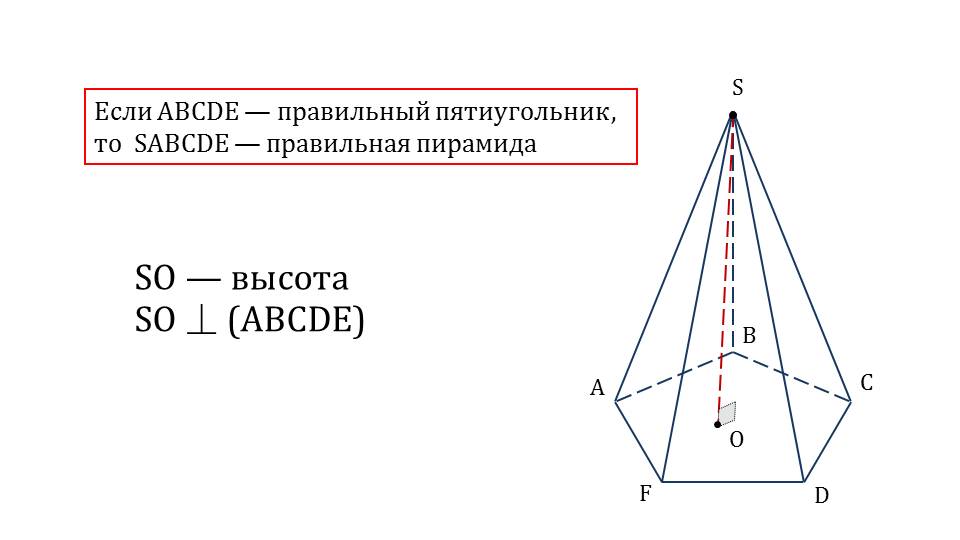
Демонстрация начинается с построения призмы ABCDEFA1B1C1D1E1F1, и пирамиды ABCDS. Оба многогранника называются правильными, если в из основе лежит правильный многоугольник. На следующем слайде правильная пирамида рассматривается более подробно. На рисунке изображена пирамида ABCDFS, в основе которой лежит правильный пятиугольник ABCDF, поэтому пирамида ABCDFS является правильной. Из вершины S на основание пирамиды опускается высота SО. Отмечается, что она является перпендикуляром к основанию пирамиды.
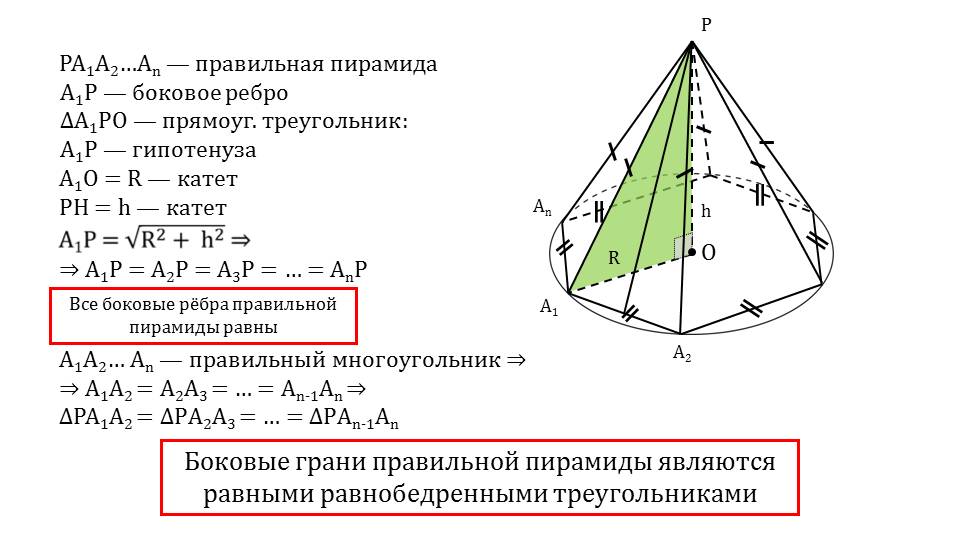
На слайде 4 рассматриваются свойства правильной пирамиды PA1A2…An, в основе которой лежит произвольный правильный многоугольник A1A2…An. На рисунке изображена пирамида с данным основанием, боковое ребро которой А1Р. Из вершины Р на основание опускается перпендикуляр РО, который с ребром РА1 и отрезком, что соединяет основание высоты и вершину А1, образует треугольник ΔА1РО. Данный треугольник - прямоугольный, у которого РА1 является гипотенузой, а А1О=R – катет и РН – катет. Очевидно, если многоугольник основания правильный, то расстояния от центра О многоугольника до его вершин будет одинаковым А1Р=√(R2+h2), поэтому все его ребра А1Р= А2О= А3О=…= АnО. Из этого следует, что боковые ребра правильной пирамиды являются равными. Также из равенства сторон многоугольника, лежащего в основании пирамиды, следует равенство боковых граней пирамиды. Этот вывод также выведен на слайде 4 для запоминания. Параллельно ходу рассуждения о свойствах пирамиды на рисунке добавляются и выделяются необходимые элементы.
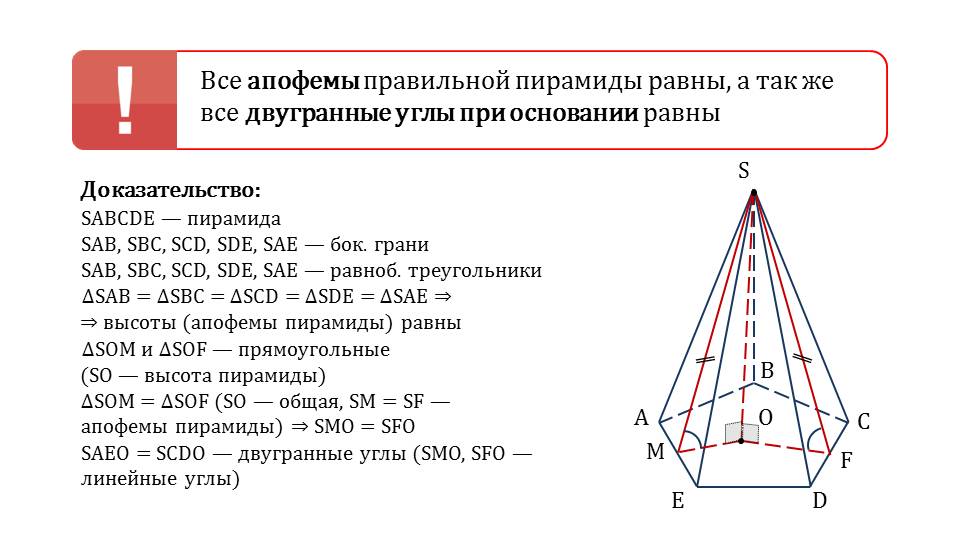
Далее рассматривается утверждение о том, что в правильной пирамиде апофемы равны и двугранные углы, образованные при основании. Доказательство теоремы сопровождается рисунком, на котором изображена правильная пирамида ABCDES. К ребрам основания проводятся опущенные из вершины S апофемы. В начале доказательства отмечается, что в правильной пирамиде каждая грань представляет собой равнобедренный треугольник. Из равенства этих треугольников следует, что высоты данных треугольников также равны. Треугольники, образованные апофемой, высотой, проведенной из вершины S к основанию пирамиды, и отрезком соединения основания апофемы с центром основания, равны по общей стороне, апофемам, отрезкам основания. Из равенства треугольников следует равенство их углов при основании. Следовательно, двугранные углы правильной пирамиды также равны.
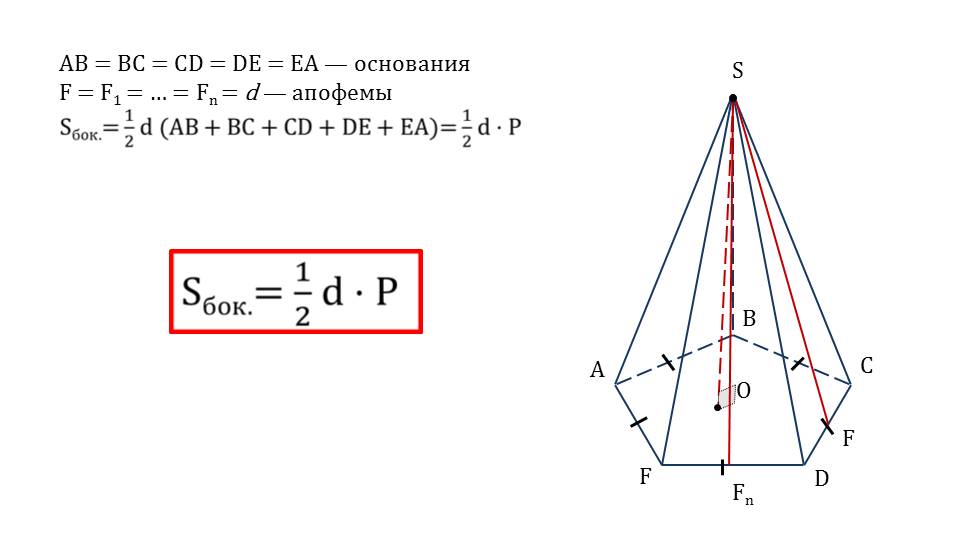
На слайде 6 рассматривается площадь боковой поверхности некоторой правильной пирамиды. Отмечается, что зная равенство ребер многоугольника, лежащего в основании, можно утверждать и о равенстве апофем правильной пирамиды. Применяя формулу для нахождения площади треугольника с учетом количества граней пирамиды, определяем Sбок.=(1/2)d(AB+BC+CD+DE+EA)=(1/2)d·P. Таким образом, формула для вычисления площади боковой поверхности Sбок.=(1/2)d·P. Формула выделена в рамку и рекомендована для запоминания.
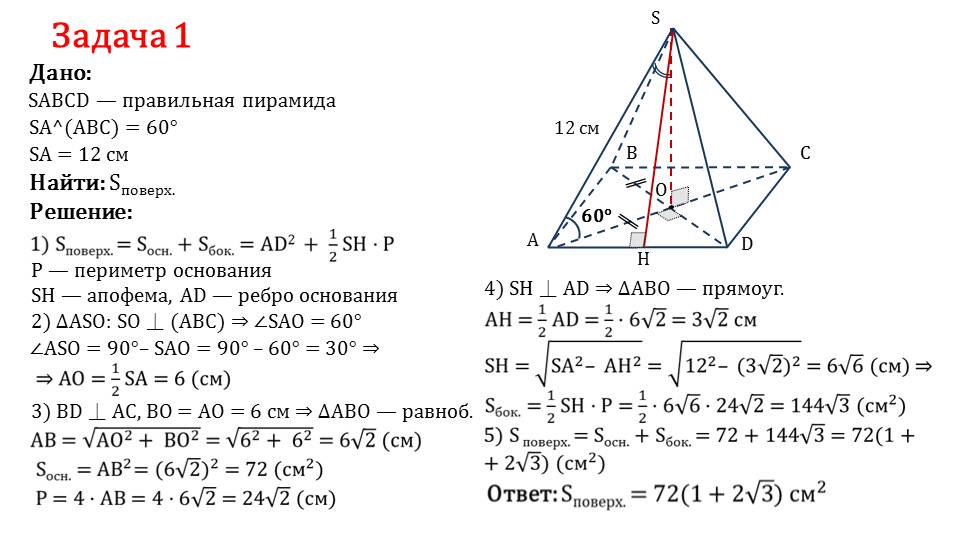
Описывается решение задачи 1, в которой дана правильная пирамида SABCD, в которой известен угол, образуемый ребром SA с основанием пирамиды SA^(ABC)=60°. Длина ребра SA=12 см. Необходимо найти площадь поверхности пирамиды. Для решения задачи потребуется найти сумму площади боковой поверхности пирамиды и площади ее основания. При этом площадь основания-квадрата определяется как AD2, а площадь боковой поверхности (1/2)SH·P, в которой Р – периметр основания, SH – апофема, AD – ребро основания. Рассматривая образованный ребром AS, высотой и полудиагональю основания прямоугольного треугольник ΔASO, и используя теорему о сумме углов треугольника, отмечаем, что угол ∠SAO=60°, а угол ∠ASO=30°. Поэтому АО=(1/2) SA=6 см. также отмечается, что треугольник, образованный половинами диагоналей основания и ребром, равнобедренный, поэтому АВ=√(АО2+ВО2)=6√2. Отсюда площадь основания Sосн.=АВ2=72 см2, а периметр Р=4·АВ=24√2 см. Из треугольника ΔSAH находим апофему SH=√(SA2-АН2)=6√6 см. Подставляя найденные значения , получаем площадь поверхности Sбок.=144√3 см2. Сложив площади боковой поверхности и основания, получаем, что полная площадь поверхности Sповерх.=72(1+2√3) см2.
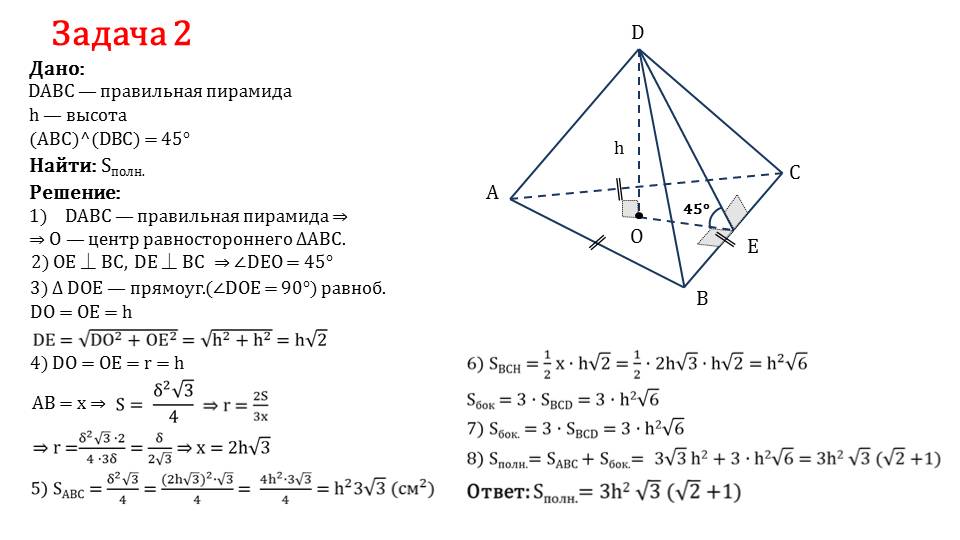
На последнем слайде представлено описание решения задачи 2, в которой дана правильная пирамида DABC, в которой высота h, а угол между основанием и боковой гранью (ABC)^(DBC)=45°. Необходимо найти полную площадь поверхности фигуры. Решение сопровождается рисунком, на котором представлена пирамида, отмечена ее высота, апофема, отрезок соединения основания высоты и апофемы. Также обозначены равные стороны, образованные прямые углы. Доказательство начинается с того, что отмечается точка О как центр равностороннего треугольника ΔАВС – основания пирамиды. Перпендикулярность к ребру ВС апофемы DE и отрезка ОЕ означает, что ∠DEO=45°. Так как треугольник ΔDEO является прямоугольным и равнобедренным, то DE=√(DO2+OE2)=h√2. Используя равенство сторон многоугольника основания, равенство катетов треугольника ΔDEO и формулу вписанной окружности, находим, что сторона треугольника основания равна 2h√3. Отсюда площадь основания SABC=h23√3 см2. Зная длину стороны основания, находим площадь поверхности Sбок.=3· SCBD=3· h2√6 Полная площадь поверхности равняется Sполн.= 3h2√3(√2+1). Задача решена.
Презентация «Правильная пирамида» может использоваться на уроке геометрии как наглядное пособие, повышающее эффективность традиционного урока. Как средств наглядности, презентация может послужить учителю, осуществляющему дистанционное обучение. Можно рекомендовать пособие ученикам для самостоятельного рассмотрения, если они требуют дополнительных занятий или осваивают тему самостоятельно.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 7971 |
| Номер материала | 902 |