
Презентация "Призма"

Краткое описание документа:
Презентация «Призма» представляет учебный материал по теме на уроке геометрии. Призма изучается более углубленно в курсе 10 класса, чем в предыдущих классах. В ходе демонстрации представляется понятие призмы, отмечаются ее элементы, определяется, каким образом вычисляется площадь боковой поверхности, описывается решение задач с применением знаний о свойствах призмы. С помощью данного пособия учителю легче решить задачи урока, сформировать представление о призме, научить решать задачи с применением изученных свойств призмы.
Презентация является одной из наиболее эффективных форм наглядности представления учебного материала по данной теме. Стереометрические тела имеют объем, из-за чего их тяжелее изображать на плоскости, чем плоские фигуры. С помощью презентации за счет анимационных эффектов и возможности делать четкие понятные построения, демонстрировать иллюстрации, легче продемонстрировать свойства объемных фигур. Возможность использовать различные цвета дает возможность выделять детали построения или понятия в формулировках, что способствует запоминанию материала.
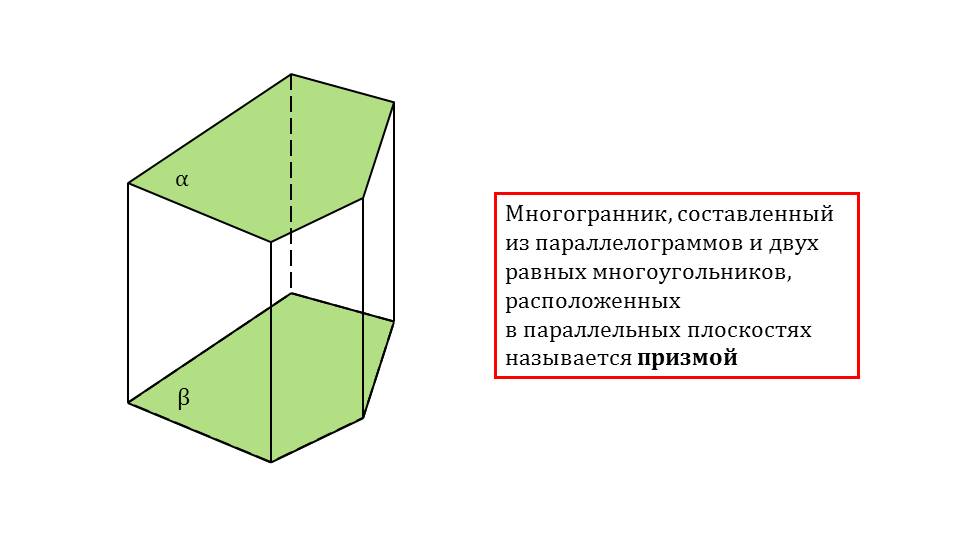
Демонстрация начинается с представления тетраэдра как одного из видов многогранника, изученного ранее. Далее напоминается понятие призмы. На рисунке изображается призма, основание которой составляют неправильные пятиугольники, очерченные на плоскостях α и β, а ее соответствующие вершины соединены отрезками. Рядом с рисунком дано определение призмы как многогранника, составленного из параллелограммов, а также двух многоугольников, что расположены в параллельных плоскостях. Данное определение выделено и заключено в рамку.
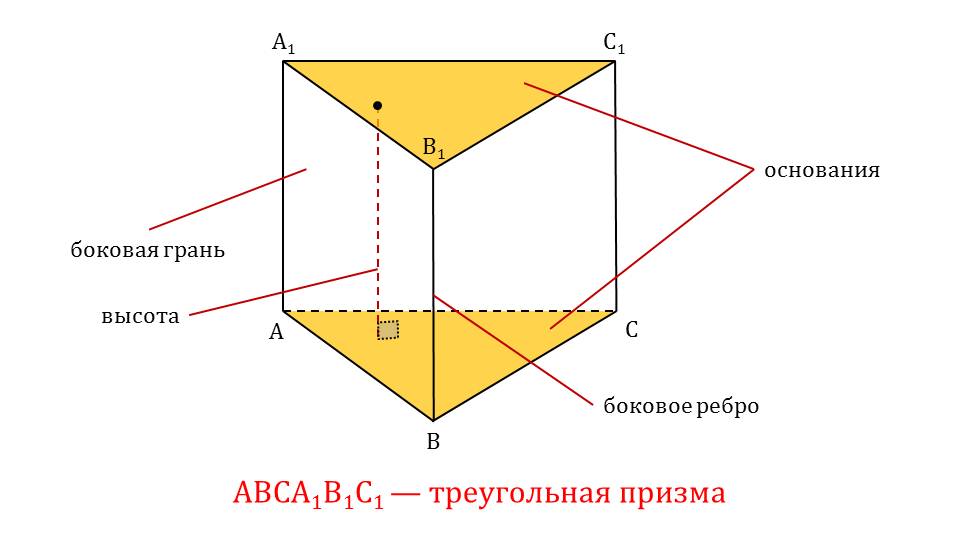
На слайде 3 представлена призма ABCDA1B1C1D1, основания которой являются двумя равными треугольниками, соответствующие вершины которых соединены отрезками. Рисунок подписан, отмечая, что ABCDA1B1C1D1 - треугольная призма. В многограннике отмечены его элементы. С помощью указателей выведены названия элементов – боковая грань, ребро, высота, два основания ΔАВС и ΔА1В1С1. На основании А1В1С1 отмечена точка, от которой опущен перпендикуляр на основание ΔАВС, формируя проекцию точки.
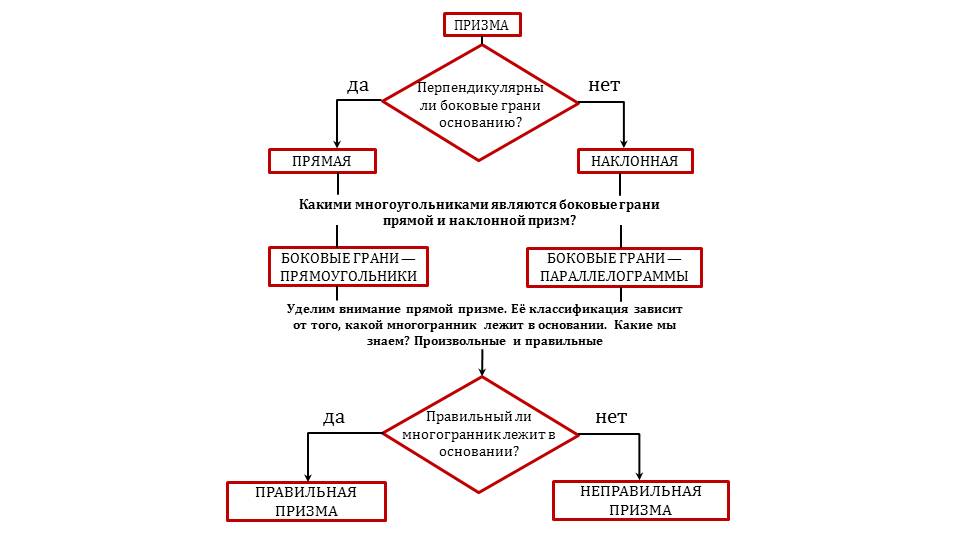
Далее представляется алгоритм, по которому определяется вид призмы. В алгоритме предусматривается проверка двух условий, по которым определяется вид призмы. Сначала проверяется перпендикулярность боковых граней, по которым определяется, призма является прямой или наклонной. Если боковые грани перпендикулярны основанию, призма прямая, иначе – наклонная. Если рассматриваемая призма прямая, то боковые ее грани являются прямоугольниками, в противном случае - параллелограммами. Далее в прямой призме проверяется условие, является ли многоугольник основания правильным. Если этот многоугольник правильный, то призма является правильной, иначе – неправильной.
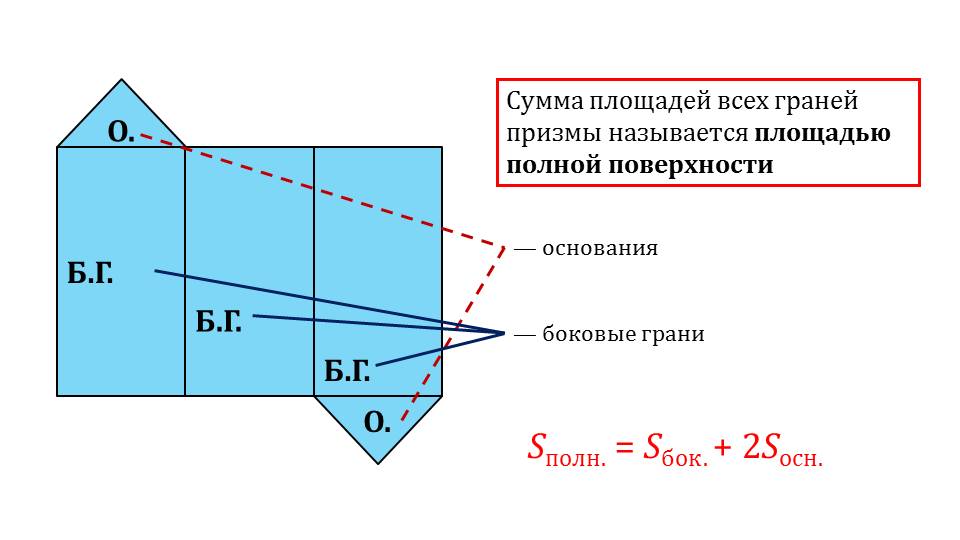
На пятом слайде представляется развертка треугольной призмы, которая состоит из двух треугольников и трех прямоугольников. Рядом с разверткой дается определение площади поверхности треугольной призмы как суммы площадей ее граней. На рисунке с помощью указателей выведены названия элементов развертки – боковые грани, основания. Также демонстрируется формула для нахождения полной площади ее поверхности как сумма площади боковой поверхности и 2-х оснований призмы Sполн.=Sбок.+2Sосн.

На слайде 6 представлена теорема, представляющая формулу для вычисления площади боковой поверхности и ее доказательство. В начале слайде сформулирована теорема о том, что площадь боковой поверхности некоторой прямой призмы равняется произведению высоты на периметр основания. Теорема выделена в рамку и рекомендована для запоминания. Под теоремой изображена призма, основанием которй служит треугольник со сторонами а1, а2 и а3, а также стороной h. Рассматривается, как находится площадь боковой поверхности призмы. Зная, что площадь прямоугольника вычисляется произведением двух измерений, подставив их, получаем Sбок.= а1·h+ а2·h+ а3·h+… аn·h. Вынеся общий множитель за скобки, получаем произведение периметра призмы на высоту. В результате преобразований получили формулу для вычисления площади боковой поверхности Sбок.= Pосн.·h. Формула выделена в рамку и рекомендована для запоминания.
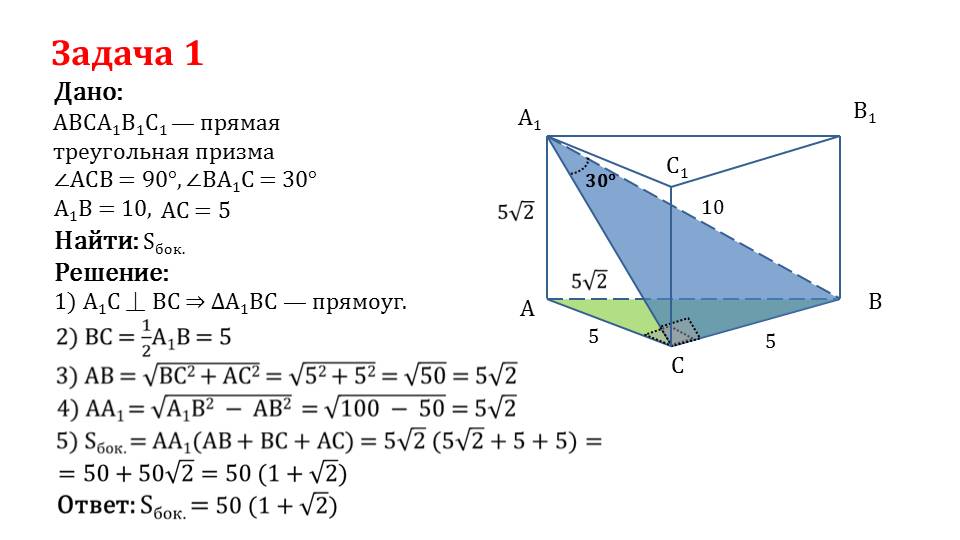
Далее описано решение задачи, в которой необходимо найти площадь боковой поверхности треугольной прямой призмы. В задаче дана прямая треугольная призма ABCDA1B1C1D1, основанием которой есть прямоугольный треугольник, в котором ∠АСВ=90°, ∠ВА1С=30°, А1В=10 и АС=5. Перпендикулярность диагонали грани А1В к стороне основания ВС означает, что треугольник Δ А1ВС является прямоугольным. При этом ВС=(1/2) А1В=5. Из прямоугольного треугольника следует АВ=√(ВС2+АС2)=5√2, а АА1=√(А1В2-АВ2)=5√2. Имея значение всех необходимых элементов, можем найти площадь боковой поверхности Sбок.= АА1(АВ+В+АС)=5√2(5√2+5+5)=50(1+√2). Задача решена.
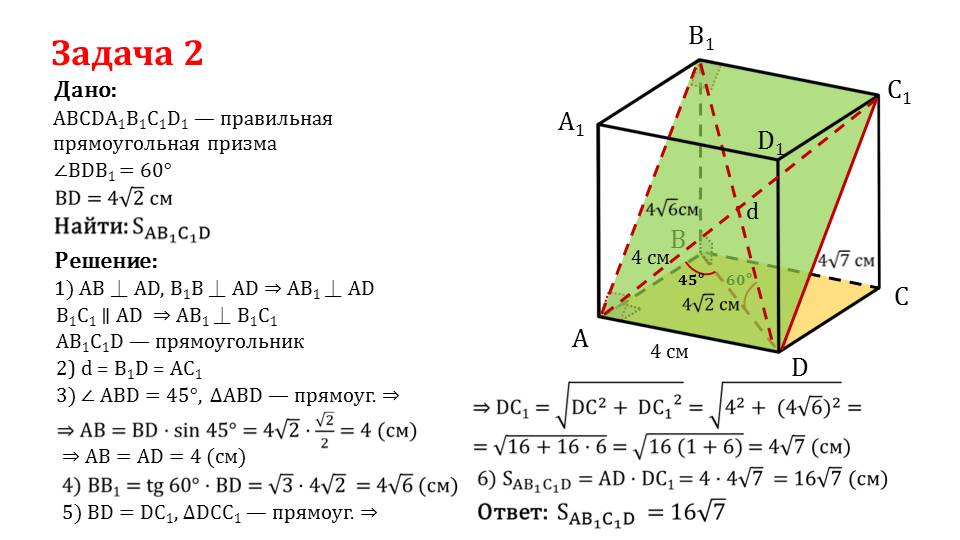
В последнем слайде описывается решение задачи, где необходимо найти площадь диагональной грани правильной прямоугольной призмы ABCDA1B1C1D1, при том, образованный диагональю угол ∠BDB1=60°, а длина диагонали BD=4√ см. Решение задачи сопровождается рисунком, на котором изображена призма ABCDA1B1C1D1, пунктирной линией отмечены ее диагонали боковых граней и самой призмы. Из перпендикулярности ребер основания и боковых ребер к ребрам основания следует перпендикулярность диагонали АВ1 к ребру основания AD. А из параллельности ребер верхнего и нижнего оснований В1С1 и AD следует перпендикулярность диагонали АВ1 к ребру верхнего основания В1С1. Отмечается, что четырехугольник AB1C1D является прямоугольником, а B1Dи АС1 – его диагонали. Из этого следует, что ∠ABD=45°, а из прямоугольного треугольника ΔABD можно найти АВ=BD·sin45°=4 см. Следовательно, АВ=AD=4 см. Боковое ребро призмы ВВ1=tg60°·BD=4√6 см. А из прямоугольного треугольника ΔDCC1 можно найти DC1=√(DC2+DC12)=4√7. Теперь можно найти площадь прямоугольника SAB1C1D=AD·DC1=16√7.
Презентация «Призма» может применяться для повышения эффективности традиционного урока в школе по данной теме. Также наглядное пособие может пригодиться учителю, осуществляющему дистанционное обучение. Наглядный материал может быть рекомендован ученикам, которые требуют дополнительных занятий для более глубокого понимания темы или изучают предмет самостоятельно.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 23617 |
| Номер материала | 900 |