
Презентация "Признак перпендикулярности двух плоскостей"

Краткое описание документа:
Презентация «Признак перпендикулярности двух плоскостей» является наглядным пособием для представления учебного материала по теме. В ходе презентации ученикам демонстрируются примеры практического использования изучаемого материала в жизни, рассматриваются свойства двугранного угла, перпендикулярность плоскостей, доказывается важная теорема по теме, описывается решение задачи с использованием изученных теоретических сведений. Презентация помогает учителю удержать внимание учеников на изучении предмета, представляет в более удобном для понимания виде учебный материал. Таким образом, учителю легче формировать умение решать задачи по геометрии.
С помощью анимации в демонстрируемых построениях лучше видны важные детали рисунка, есть возможность сопровождать ход доказательства построением необходимых элементов. В презентации широко применяется выделение цветом, благодаря которому выделенные понятия легче запоминаются. Использование комплекса приемов помогает учителю повысить эффективность урока геометрии, быстрее достичь учебных целей.


Прежде чем представить признак перпендикулярности плоскостей, ученикам напоминается понятие плоскости. На примере обычного обеденного стола представлена плоскость. Далее представлены две пересекающиеся плоскости, место пересечения которых отмечено прямой. В данном случае это перпендикулярно расположенные плоскости. Примером перпендикулярно расположенных плоскостей могут служить открытая дверь, изображенная на рисунке, или ноутбук с открытой крышкой.

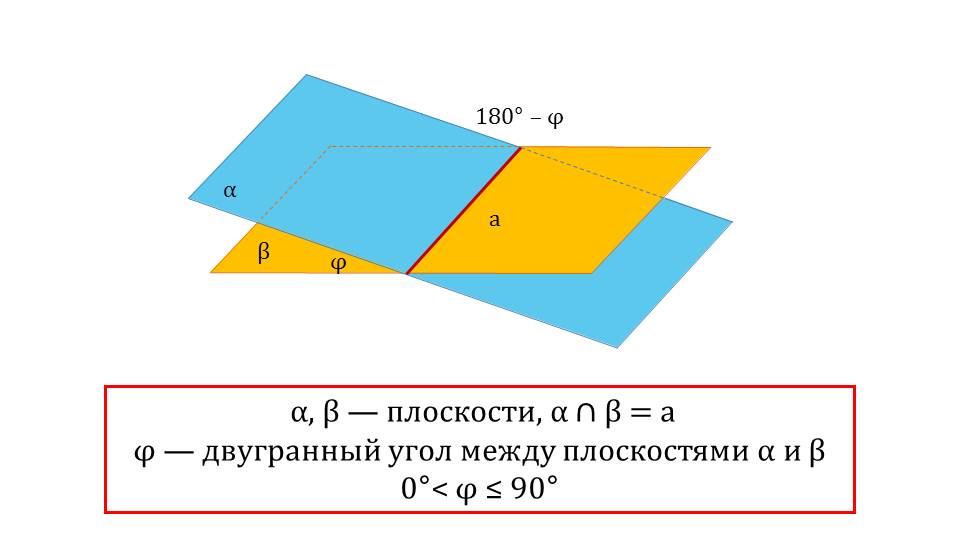
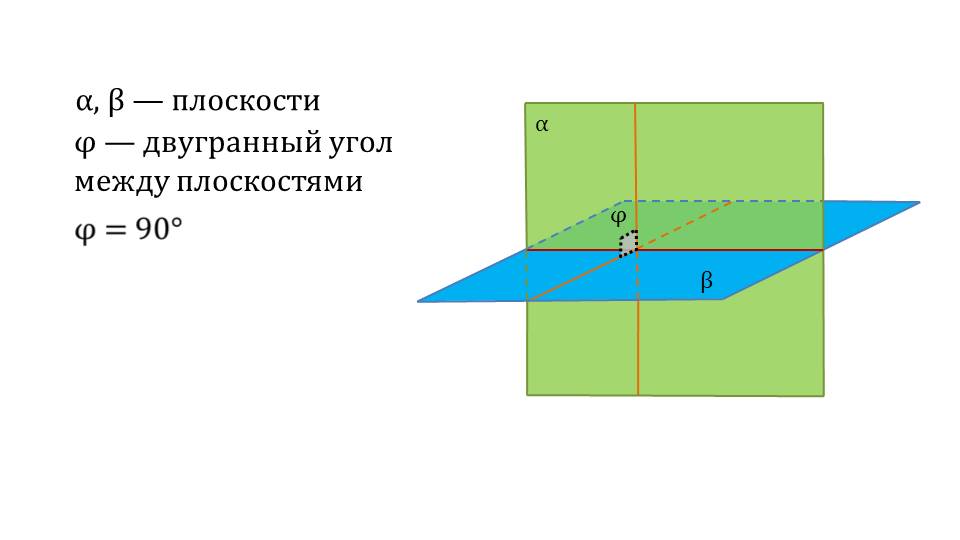
На следующем слайде изображены две плоскости α и β, место пересечения которых представляет собой прямую а. Плоскости образуют между собой 4 угла, которые попарно равны. Один из углов отмечен как φ, а величина второго угла 180°-φ. Ниже рисунка отмечается, что при пересечении по прямой а плоскостей α и β образуется двугранный угол φ, величина которого более 0° и менее или равна 90°. Далее представляется пересечение плоскостей α и β, которые образуют угол 90°, то есть перпендикулярны между собой. После введения понятия дается определение перпендикулярности двух плоскостей, если величина двугранного угла, образованного двумя плоскостями, 90°. Определение сопровождается рисунком пересечения плоскостей φ и ε, которые перпендикулярны между собой. Представляется фото, демонстрирующее перпендикулярно расположенные плоскости, которые встречаются в нашей жизни, на примере стен квартиры.
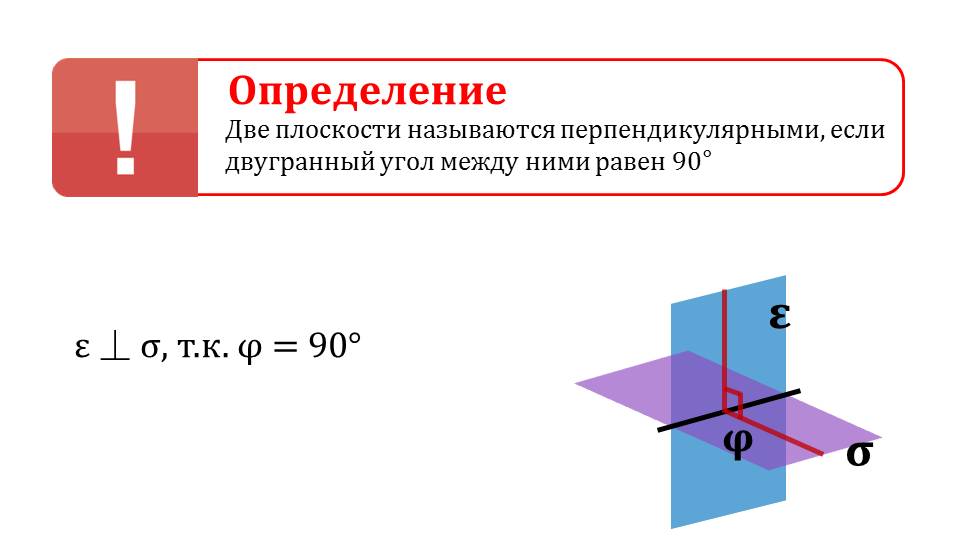
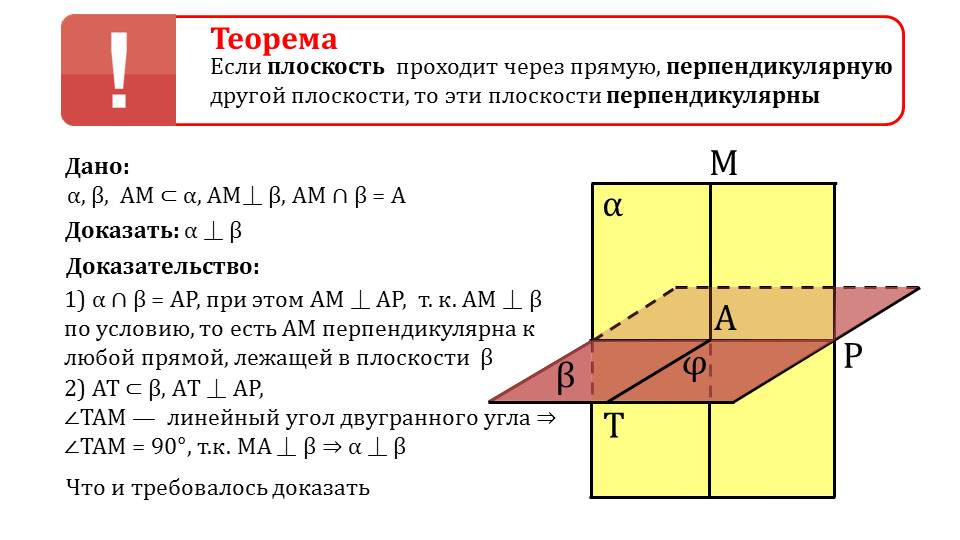
Описывается доказательство теоремы о перпендикулярности плоскостей, одна из которых проходит через прямую, перпендикулярную второй прямой. Формулировка теоремы выделена в рамку и рекомендована для запоминания. Доказательство теоремы сопровождается рисунком. На нем изображены две плоскости α и β. На плоскости α изображена прямая АМ, при этом известно, что АМ перпендикулярна β, и АМ пересекает плоскость β в точке А. Необходимо доказать перпендикулярность плоскостей α и β. Сначала отмечается, что плоскости пересекаются по прямой АР, при этом АМ перпендикулярна АР, так как АМ перпендикулярна плоскости β. АТ, принадлежащая плоскости β, перпендикулярна прямой пересечения плоскостей АР. Угол ∠ТАМ является линейным углом двугранного Так как АМ перпендикулярна плоскости β, то ∠ТАМ=90°. Теорема доказана.

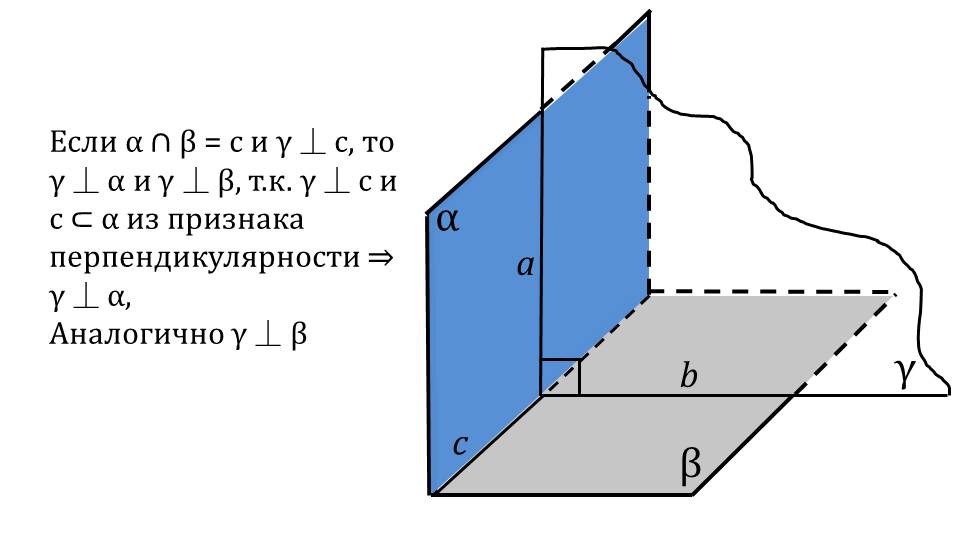
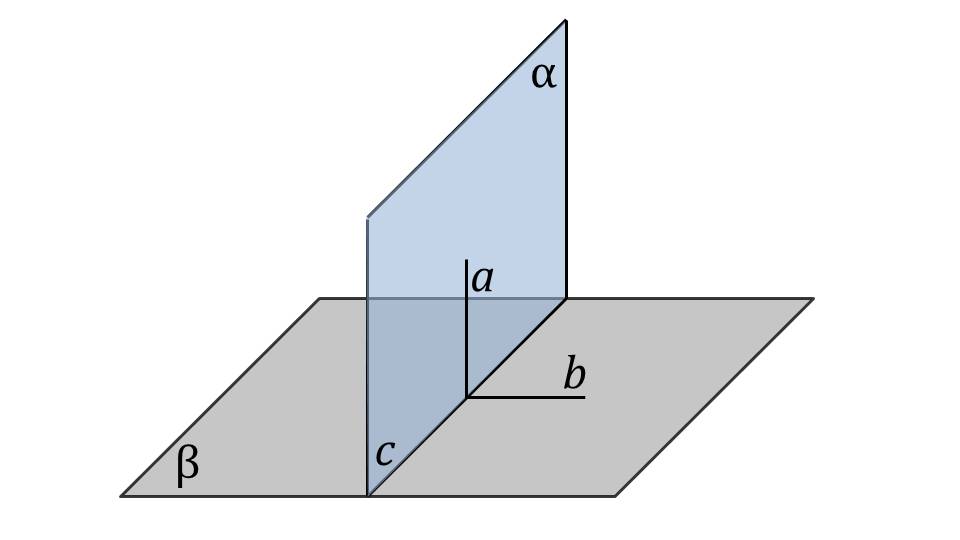
На следующем слайде изображены перпендикулярно расположенные плоскости α и β, а также пересекающая их плоскость γ. Отмечается, что если плоскости α и β пересекаются в некоторой прямой с, и эта прямая перпендикулярна плоскости γ, данная плоскость γ перпендикулярна плоскостям α и β. В доказательстве утверждения используется признак перпендикулярности, так как плоскость γ перпендикулярна с, а с принадлежит α. Отмечается, что аналогично доказывается перпендикулярность γ и β. Далее демонстрируется рисунок, на котором изображены плоскости α и β, построенные в плоскостях прямые a и b, перпендикулярные к прямой с и между собой.
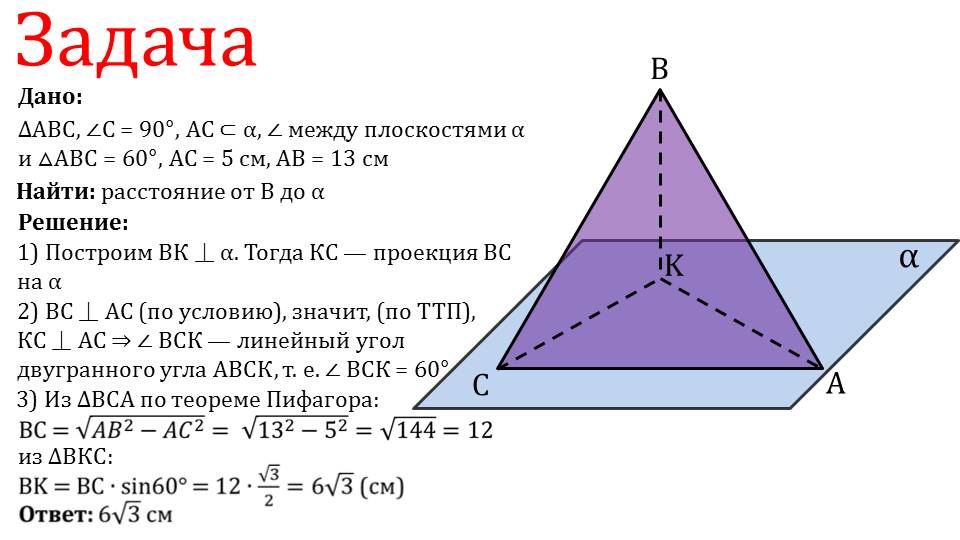
Описывается решение задачи, в которой дан треугольник ΔАВС, одна сторона которого АС расположена на плоскости α. Известно, что угол треугольника ∠С=90°, стороны АС=5 см, АВ=13 см. При этом угол между плоскостями ΔАВС и α равен 60°. Необходимо узнать расстояние от вершины треугольника В до плоскости α. Для решения задачи достраивается перпендикуляр ВК, опущенный на плоскость α. Проекцией на плоскость α наклонной ВС является отрезок КС. По условию, стороны треугольника АС и ВС перпендикулярны, поэтому КС перпендикулярна АС, следовательно, ∠ВСК является линейным углом двугранного угла АВСК. Этот угол ∠ВСК=60°. Так как треугольник ΔВСА прямоугольный, по теореме Пифагора, ВС=√(АВ2-АС2)=√(132-52)=12. Теперь находим искомое расстояние ВК=ВС·sin 60°=12·√3/2=6√3. Задача решена.
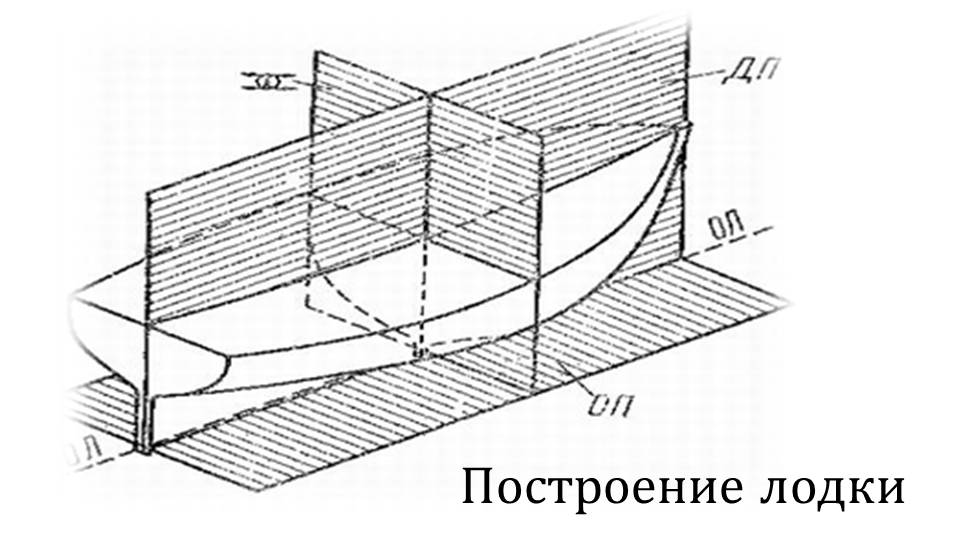
Далее демонстрируется использование перпендикулярных плоскостей в жизни. Примером служит схема строительства лодки. Перпендикулярные плоскости составляют основу, вокруг которой возводятся остальные элементы. Также полученные теоретические знания применяются в строительстве мостов. На фото представлен мост, конструкция которого предполагает использование свойств перпендикулярных плоскостей. Также степени представляют собой сооружение, удобство в эксплуатации которого обусловлено перпендикулярным расположением плоскостей.


Презентация «Признак перпендикулярности двух плоскостей» предназначена для проведения урока геометрии в школе. Также пособие, наглядно представляющее учебный материал, можно использовать учителю, осуществляющему дистанционное обучение. Пособие можно рекомендовать ученикам, которым требуются дополнительные занятия для более глубокого понимания изучаемой темы.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 18206 |
| Номер материала | 895 |