
Презентация "Признак перпендикулярности прямой и плоскости"

Краткое описание документа:
Презентация «Признак перпендикулярности прямой и плоскости» представляет наглядный материал для освоения темы на уроке геометрии. С помощью презентации учитель дает представление о перпендикулярности прямой плоскости, формирует умение решать задачи с применением теоретических знаний о перпендикулярности плоскости и прямой. В ходе презентации на примере раскрывается понятие перпендикулярности плоскости и прямой, формулируется определение плоскости и прямой, доказывается важная теорема о перпендикулярности двух параллельных прямых плоскости и обратная к ней, описывается решение двух задач с использованием теоретических знаний о перпендикулярности прямой и плоскости.
Представление материала в форме презентации имеет преимущество по сравнению с другими способами. В ходе демонстрации применяются анимационные эффекты, позволяющие структурировать подачу информации, более понятно преподнести объяснение процессов и преобразований при построении геометрических фигур, сделать объяснение решения задач более доступным. Текст определения или теоремы легче запоминать, если он на экране выделен цветом, к нему приложены иллюстрации или схемы. Все эти приемы предоставляют возможность более эффективного воздействия на мыслительные процессы учеников, запоминание и понимание материала.
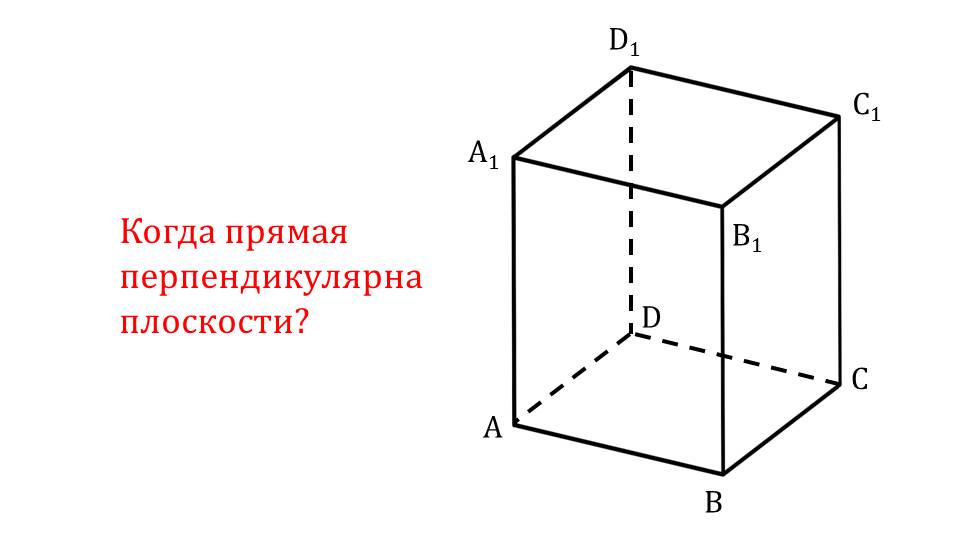
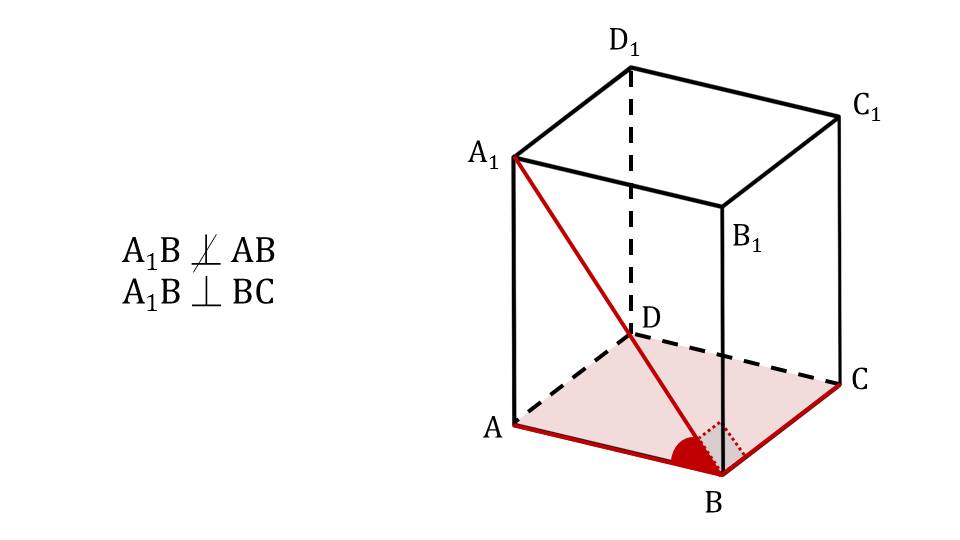
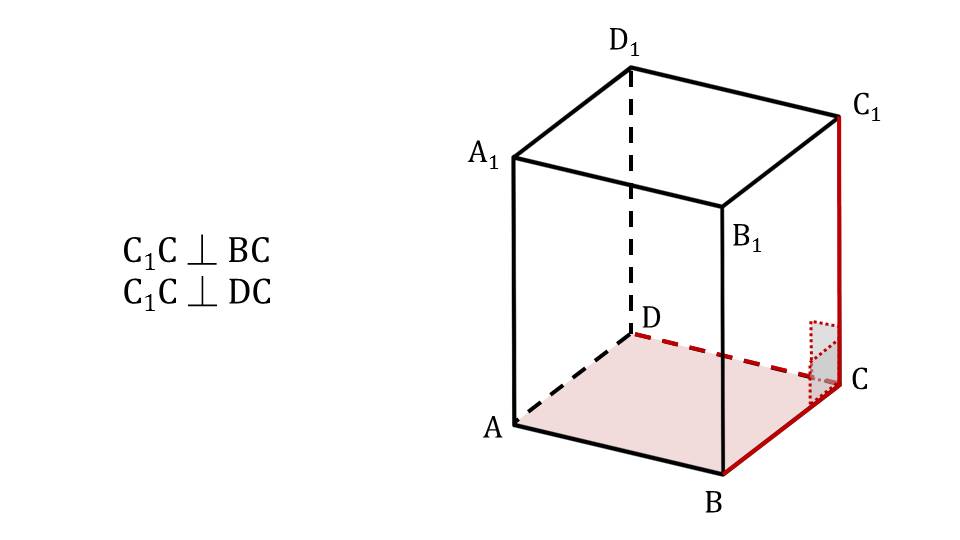
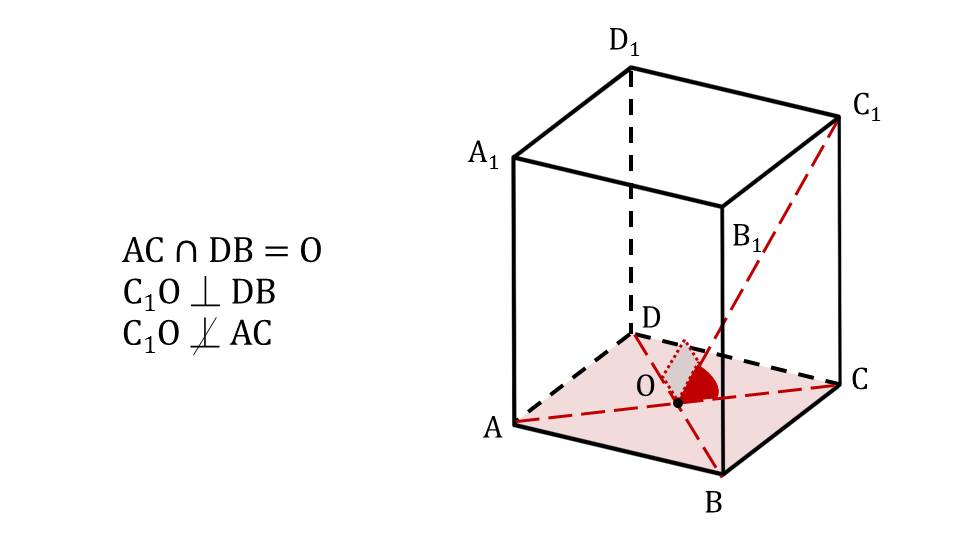
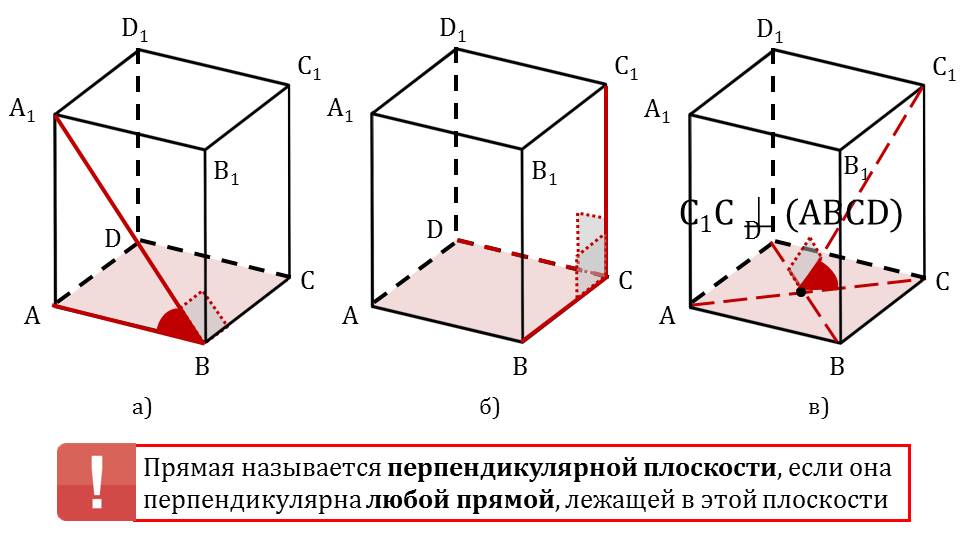
Презентация начинается с демонстрации параллелепипеда как объемной геометрической фигуры, с помощью которой можно демонстрировать свойства объектов в пространстве. На рисунке изображен прямоугольный параллелепипед ABCDA1B1C1D1. На экране отображается вопрос, на который отвечает данный учебный материал – когда прямая перпендикулярна плоскости? В данном параллелепипеде строится отрезок А1В, который является диагональю одной из граней АВA1B1. По отношению к прямой АВ построенный отрезок не является перпендикулярным. С прямой, содержащей отрезок ВС, диагональ A1B составляет угол 90°, поэтому является к ней перпендикулярной. На рисунке построенная диагональ и рассматриваемые ребра основания параллелепипеда выделены красным цветом, рядом с рисунком демонстрируется обозначение взаимного расположения рассматриваемых ребер. На следующем слайде выделено боковое ребро СС1 и ребра основания ВС и CD. Обозначен прямой угол, образуемый между каждым ребром основания и боковым ребром. Это дает основания утверждать, что боковое ребро перпендикулярно к ребрам основания. Рядом с рисунком этот факт обозначен выражениями СС1﬩ ВС и СС1﬩ CD. На слайде 4 рассматривается взаимное положение диагоналей основания АС и BD и прямой, проведенной из вершины С1 к точке пересечения диагоналей основания О. На рисунке обозначено, что С1О с диагональю АС составляет некоторый угол, отличный от прямого. В то же время к диагонали DB прямая С1О расположена под углом 90°. Рядом с рисунком указано взаимное расположение прямых АС﬩ С1О и DB﬩ С1О при том, что О – точка пересечения АС и DB.
На слайде 5 демонстрируется анализ взаимного положения прямых и плоскостей в прямоугольном параллелепипеде на основании анализа, который сделан был при рассмотрении взаимного положения ребер. Отмечается, что на первом рисунке прямая А1В является перпендикулярна только к одному ребру основания, на втором боковое ребро перпендикулярно к ребрам основания, и на третьем - С1О перпендикулярно к одной диагонали основания и не перпендикулярно к другой. Ниже рассмотренный случаев отображается определение перпендикулярности прямой и плоскости. Отмечается, что прямая будет перпендикулярна плоскости в случае, когда она перпендикулярна всякой прямой рассматриваемой плоскости. На следующем слайде выделены боковые ребра параллелепипеда, каждое из которых перпендикулярно основанию ABCD.
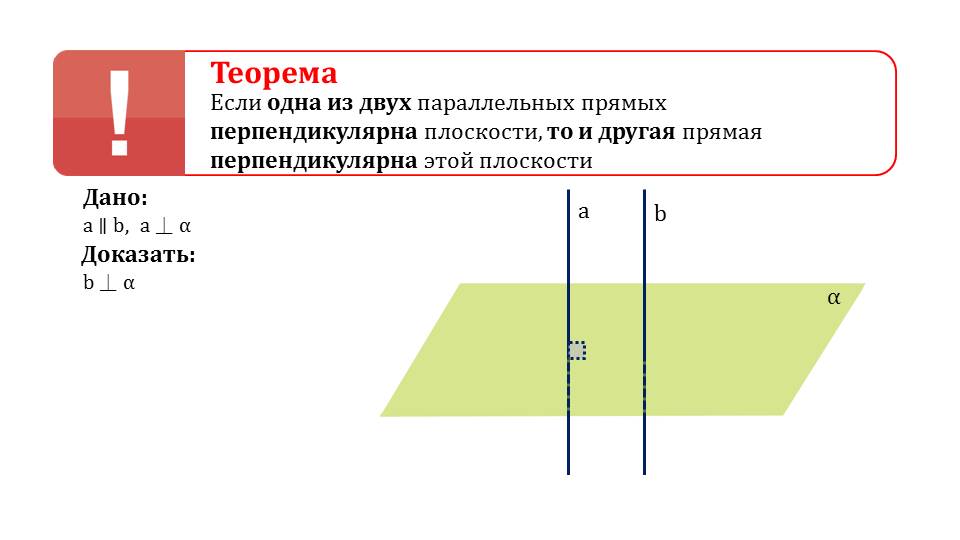
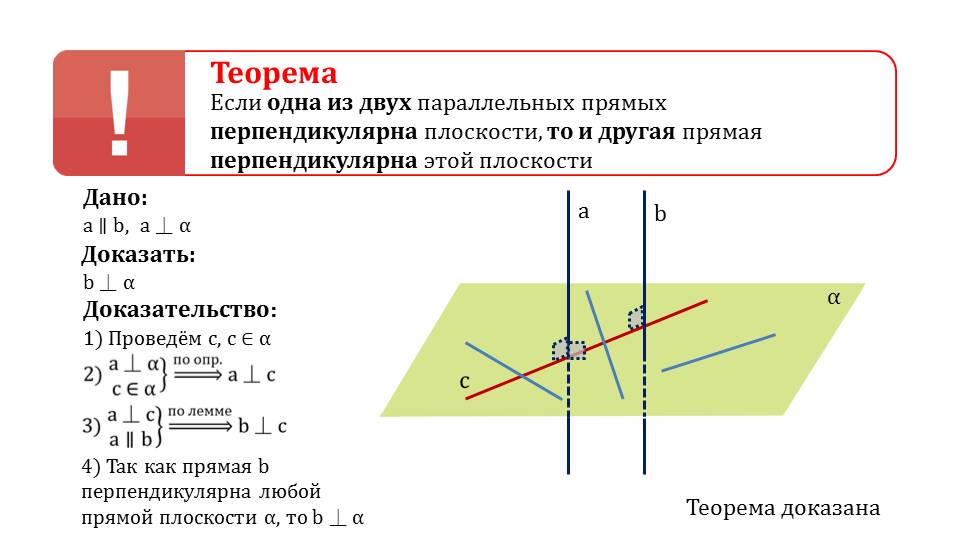
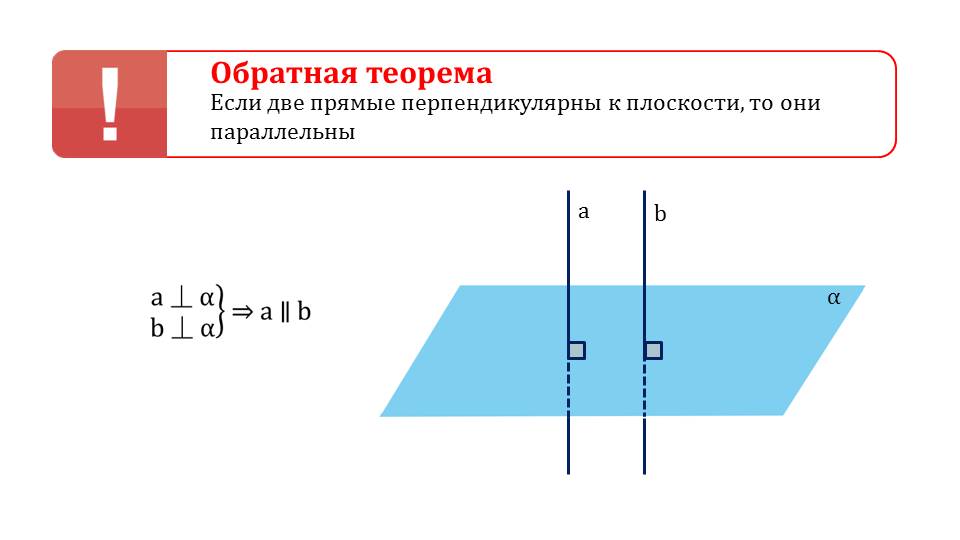
Далее демонстрируется формулировка теоремы, утверждающей о перпендикулярности некоторой плоскостей обеих параллельных прямых, если одна из них перпендикулярна этой плоскости. Доказательство начинается с построения двух параллельных прямых a и b, проходящих через плоскость α. При этом обозначено, что прямая a составляет с плоскостью α прямой угол. Необходимо доказать b﬩α. Для этого проводится вспомогательная прямая с, принадлежащая плоскости α. По определению перпендикулярности прямой и плоскости ясно, что а﬩с. Из того, что а﬩с и a‖b, с использованием изученной леммы, следует b﬩c. А так как прямая bперпендикулярна всякой прямой α, то b﬩а. утверждение доказано. Затем указано, что также можно доказать обратную теорему, которая утверждает о параллельности прямых, каждая из которых перпендикулярна к плоскости.

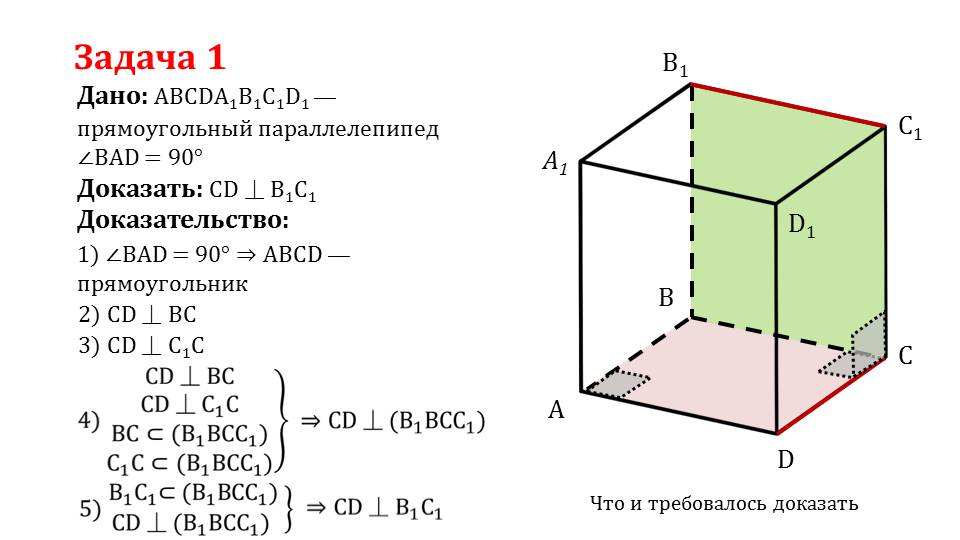
На слайде 11 описывается решение задачи, в которой дан прямоугольный параллелепипед ABCDA1B1C1D1, и где нужно доказать перпендикулярность CD и B1C1. Решение задачи демонстрируется на рисунке, где построен прямоугольный параллелепипед ABCDA1B1C1D1, в котором обозначены прямые углы ∠BAD, ∠C1CD, ∠BCD. Отмечается, что из равенства ∠BAD=90° следует, что ABCD – прямоугольник. Перпендикулярность ребра основания CD параллелепипеда ABCD к ребрам C1C и ВС означает, что данное ребро перпендикулярно плоскости СВB1C1. Перпендикулярность CD к плоскости СВB1C1 означает также, что CD перпендикулярна и к B1C1. Задача решена.
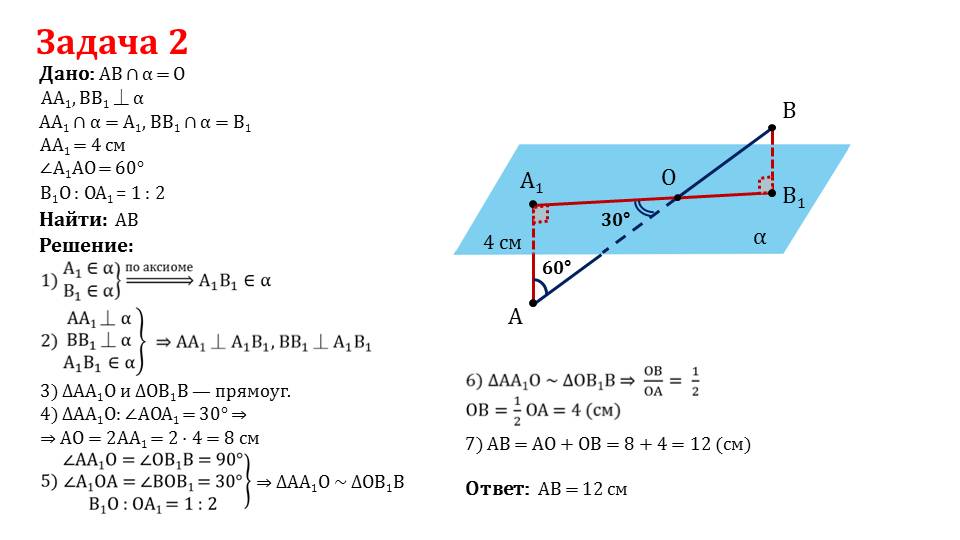
На последнем слайде описано решение задачи, в которой нужно найти расстояние между точками в пространстве А и В, которые являются концами отрезка АВ, проходящего через плоскость. На рисунке демонстрируется условие задачи – изображена плоскость α, точки А и В, соединенные отрезком. Из этих точек на плоскость опущены перпендикуляры AA1 и BB1. Длина перпендикуляра AA1=4 см, образованный угол ∠A1AО=60°. Соотношение отрезков В1О: ОA1=1:2. Так как точки A1 и B1 лежат на плоскости α, то и отрезок A1B1 также лежит на плоскости α. Из этого следует перпендикулярность опущенных на плоскость перпендикуляров AA1 и BB1 к отрезку A1B1. Полученные данные свидетельствуют о том, что треугольники ΔAA1О и ΔОBB1 являются прямоугольными. Для треугольника ΔAA1О, так как угол ∠AОA1=30°, то АО=2AA1=2·4=8 см. Равенства ∠AA1О=∠ ΔОB1B=90°, ∠A1ОA=∠ ΔBОB1=30° и соотношение В1О: ОA1=1:2 свидетельствуют о подобии треугольников ΔAA1О и ΔОB1B. Из подобия треугольников следует ОВ=(1/2)ОА=4 см. Поэтому АВ=АО+ОВ=8+4=12 см.
Презентация «Признак перпендикулярности прямой и плоскости» может применяться на уроке геометрии для повышения эффективности обучения. Также материал может стать полезным инструментом в дистанционном обучении. При необходимости презентация может рекомендоваться ученикам для самостоятельного рассмотрения темы.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 6091 |
| Номер материала | 888 |