
Презентация "Признак перпендикулярности прямой и плоскости"

Краткое описание документа:
Презентация «Признак перпендикулярности прямой и плоскости» представляет собой наглядное пособие для объяснения учебного материала по данной теме на уроке геометрии в 10 классе. В ходе презентации дается представление о практическом приложении теоретических сведений о перпендикулярности плоскости и прямой в пространстве, доказываются теоремы, необходимые для решения задач о перпендикулярности прямых и плоскости, описываются примеры решения задач, в которых применяются знания предмета. С помощью презентации учитель имеет возможность представить материал в более понятной форме для учеников, сделать наглядными построения и преобразования геометрических объектов.
Подача материала в форме презентации разнообразит ведение урока, удерживая внимание учеников на предмете изучения. В таком наглядном пособии с помощью анимационных эффектов можно представить процесс построения рисунков более живым, детальным, с выделением важных частей, особенностей, со всеми обозначениями. Также в презентации используется выделение цветом и с помощью рамки важных определений, понятий. Это способствует лучшему запоминанию теоретического материала. Использование презентации повышает эффективность обучения.

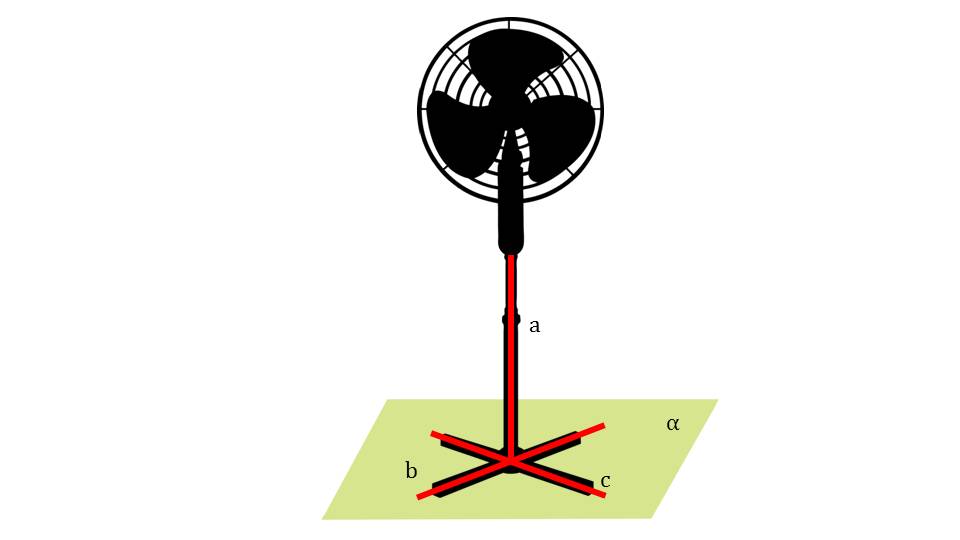
Демонстрация начинается с представления практического приложения изучаемого предмета. Ученикам рассказывается о труде инженера, которому необходимо решить задачи равновесия сил, надежной опоры предметов и множество других задач, в которых применяются свойства геометрических фигур. На следующем слайде приведен пример применения свойств перпендикулярных отрезков. В данном случае это опора вентилятора, которая решает задачу устойчивости прибора. Такая опора представляет собой модель двух пересекающихся прямых и перпендикулярной к ним обеим прямой.
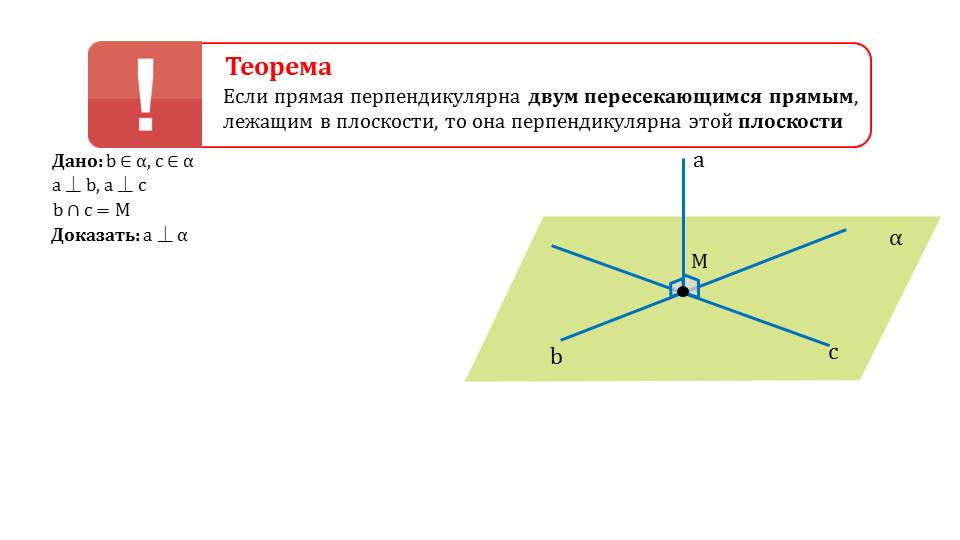
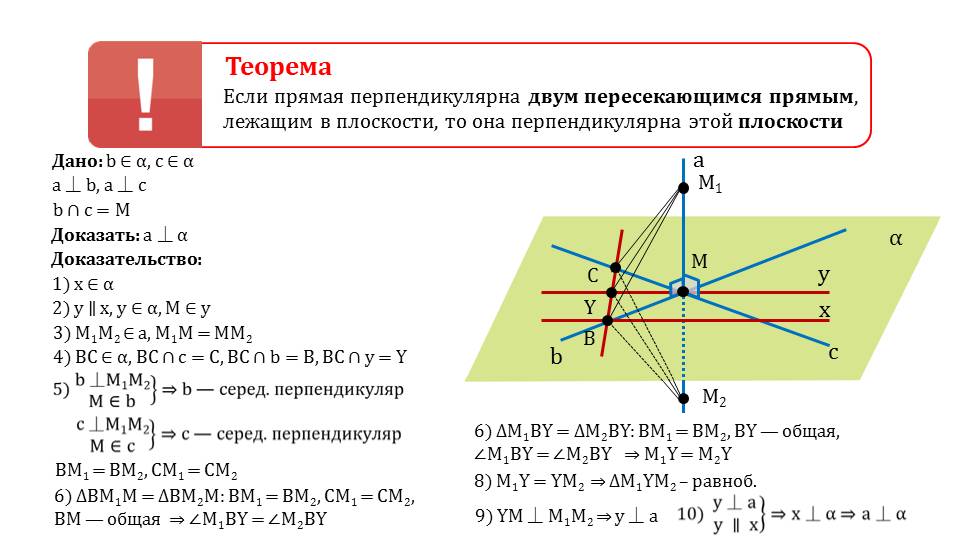
На экране демонстрируется формулировка теоремы, в которой сказано, что перпендикулярность прямой двум пересекающимся прямым означает ее перпендикулярность плоскости, содержащей их. К теореме дается изображение плоскости α и двух пересекающихся на ней прямых b и c. Из точки пересечения М данных прямых поднят перпендикуляр а. На рисунке обозначены прямые углы, которые составляет прямая а с каждой и прямых плоскости - b и c. Необходимо доказать перпендикулярность прямой а и плоскости α. Для доказательства достраивается вспомогательная прямая х, принадлежащая плоскости, и параллельная ей прямая у, проходящая через точку М. На прямой а отмечается точка М1 вверх от точки М и точка М2 на таком же расстоянии вниз от точки М. Если провести прямую ВС, пересекающую прямую b в точке В, а прямую c в точке С, а также проведенную через М прямую у в точке Y, то отмечая, что b и с являются серединными перпендикулярами, можно утверждать, что ВМ1=ВМ2, СМ1=СМ2. При этом треугольники ΔВМ1М=ΔВМ2М равны, так как соответствующие стороны ВМ1=ВМ2 равны, а Вм является общей стороной. Из этого следует и равенство углов ∠М1ВY=∠М2ВY. Таким же образом доказывается равенство треугольников ΔM1BY=ΔM2BY по равным сторонам M1B=M2B, так как BY – общая, а углы ∠М1ВY=∠М2ВY. Из равенства треугольников следует равенство расстояний М1Y=М2Y. Из равенства данных расстояний следует, что треугольник ΔM1YM2 равнобедренный. А из перпендикулярности YM и М1М2 следует перпендикулярность у и а. Так как у┴а, и у║а, то х┴α, следовательно а┴α.
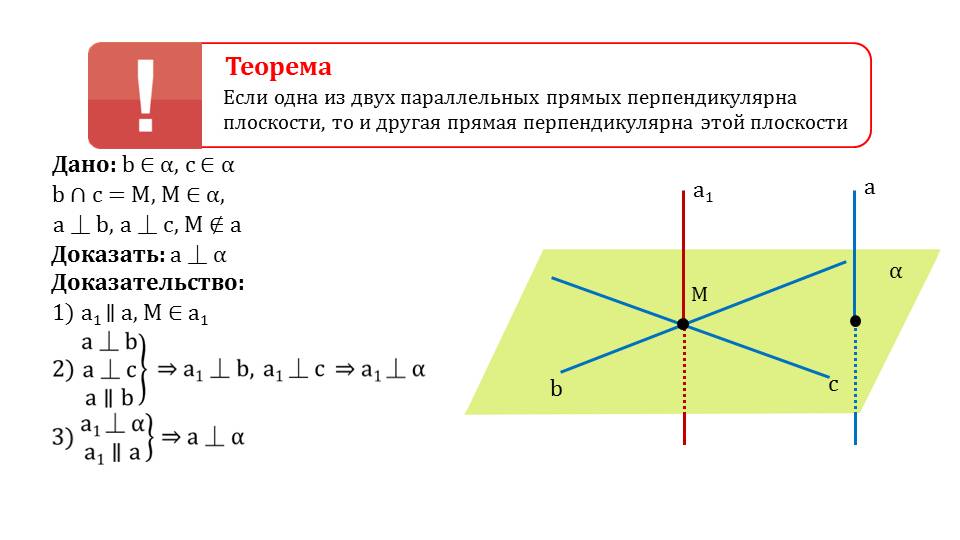
Далее доказывается теорема, в которой утверждается о перпендикулярности плоскости одной из параллельных прямых, вторая из которых перпендикулярна этой плоскости. Доказательство сопровождается рисунком, на котором изображается плоскость α с построенными на ней прямыми b и c, пересекающимися в точке М. Известно, что а перпендикулярна b и а перпендикулярна с. Нужно доказать, что прямая а перпендикулярна плоскости α. Для доказательства строится вспомогательная а1, параллельная а, но которая проходит через точку М. Так как а перпендикулярна b и с, то а1 перпендикулярна b и с, а следовательно и перпендикулярна плоскости α. К тому же если а1 перпендикулярна плоскости α и параллельна а, то а будет перпендикулярна α. Утверждение доказано.
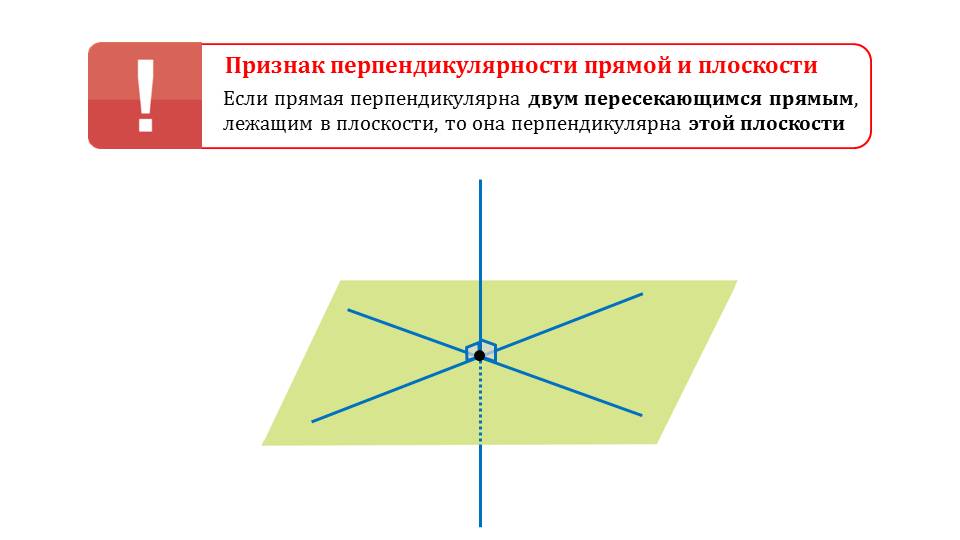
На следующем слайде представлен признак перпендикулярности прямой к плоскости, который утверждает, что прямая перпендикулярна плоскости, если она перпендикулярна пересекающимся прямым, принадлежащим данной плоскости. Теорема сопровождается рисунком, на котором изображена плоскость, на которой расположены две пересекающиеся прямые, перпендикулярные третьей прямой.
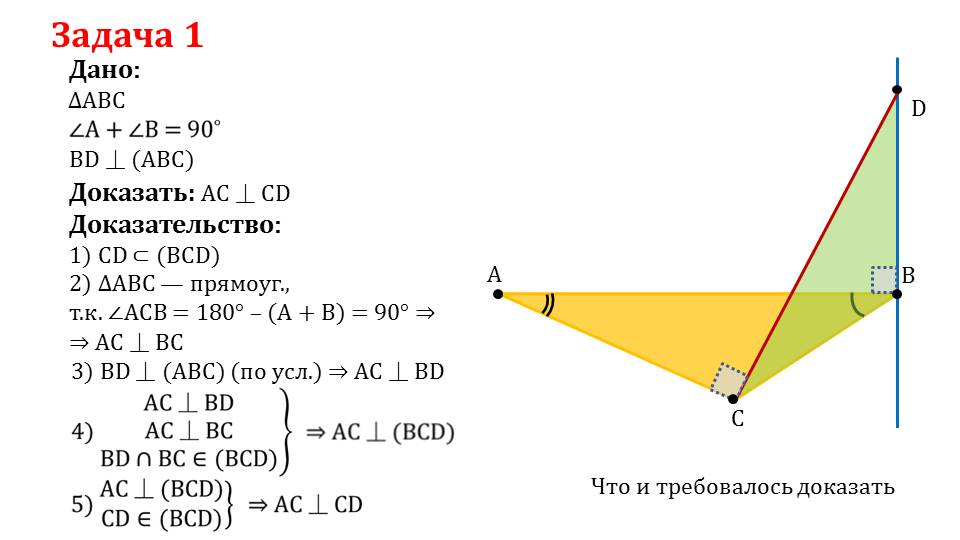
На слайде 7 представлено описание решения задачи , в которой дан некоторый треугольник ΔАВС с углами ∠А+∠В=90°, а BD перпендикулярна плоскости, содержащей треугольник ΔАВС. Необходимо доказать перпендикулярность АС и CD. Чтобы доказать справедливость утверждения, сначала отмечается, что CD принадлежит плоскости, содержащей треугольник ΔBCD.При этом ΔАВС является прямоугольным. По условию задачи BD┴(АВС), следовательно, АС┴ BD. Перпендикулярность прямой АС пересекающимся прямым BD и ВС означает что АС перпендикулярна плоскости, включающей данные прямые. Из этого факта и того, что СD также принадлежит данной плоскости следует, что СD перпендикулярна АС. Утверждение справедливо.
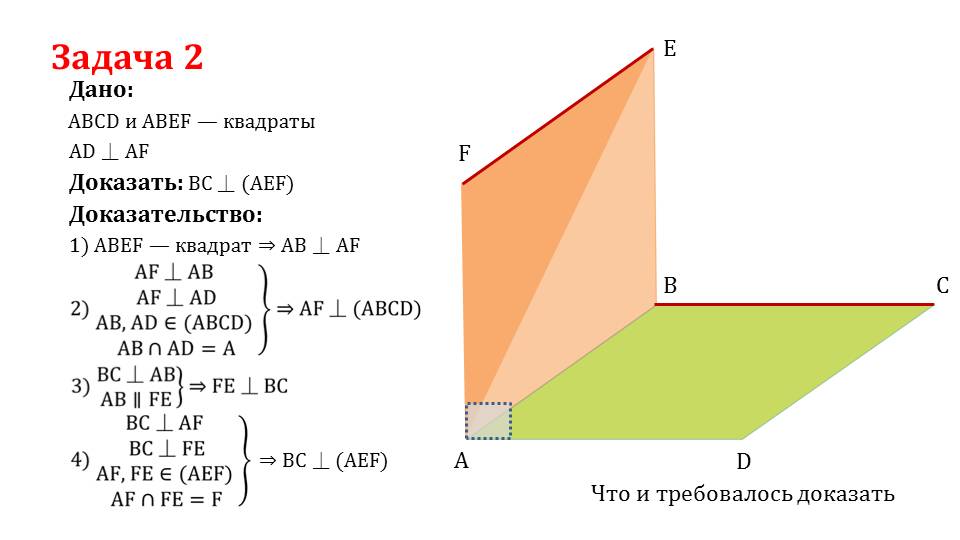
На последнем слайде доказывается перпендикулярность прямой плоскости. Условием даны квадраты ABCD и ABEF, стороны которых AD и AF находятся под углом 90° друг к другу. Необходимо доказать перпендикулярность стороны ВС к плоскости (AEF). Так как ABEF – квадрат, то стороны АВ и AF перпендикулярны. Также перпендикулярными между собой являются AF и AD. При этом АВ и AD принадлежат плоскости ABCD. Из этого следует перпендикулярность AF и плоскости (ABCD). Из перпендикулярности АВ и ВС и параллельности АВ и EF следует перпендикулярность Вс и FE. А так как ВС перпендикулярна AF и FE, принадлежащие плоскости (AEF), то ВС также будет перпендикулярна плоскости (AEF). Утверждение доказано.
Презентация «Признак перпендикулярности прямой и плоскости» может использоваться на уроке геометрии в качестве наглядного пособия. Также материал рекомендуется применять в ходе дистанционного обучения для повышения наглядности учебного материала. Презентация может быть рекомендована ученикам, изучающим предмет самостоятельно или требующим дополнительных занятий для более глубокого понимания предмета.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 8945 |
| Номер материала | 889 |