
Презентация "Прямоугольный параллелепипед"

Краткое описание документа:
Презентация «Прямоугольный параллелепипед» является наглядным пособием для проведения урока геометрии по данной теме. С помощью презентации можно углубить понятие о прямоугольном параллелепипеде, сформировать умение решать задачи, в которых применяются знания о свойствах прямоугольного параллелепипеда. В ходе презентации детально рассматривается прямоугольный параллелепипед, его виды, свойства его элементов, приводятся примеры прямоугольных параллелепипедов, встречающихся в жизни.
В презентации можно воспользоваться возможностью вставки иллюстраций, построения чертежей. Анимационные эффекты, используемые в составлении слайдов, дают возможность представить учебный материал в виде, наиболее удобном для понимания учеников. При построениях можно выделить с помощью цвета отдельные детали построения. Также цветом могут быть выделены определения, которые нужно запомнить. Использование всех этих приемов дает возможность акцентировать внимание учеников на изучении предмета, повысить эффективность обучения.

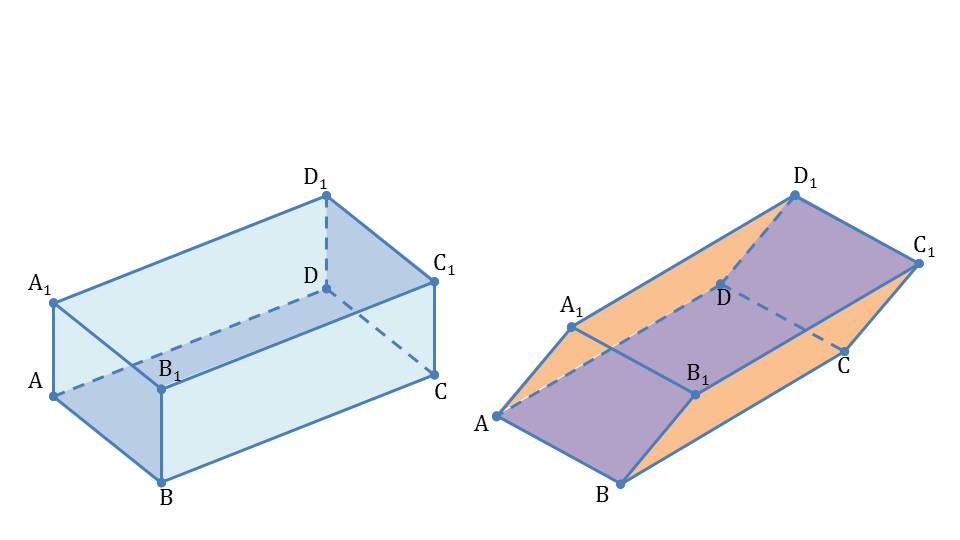
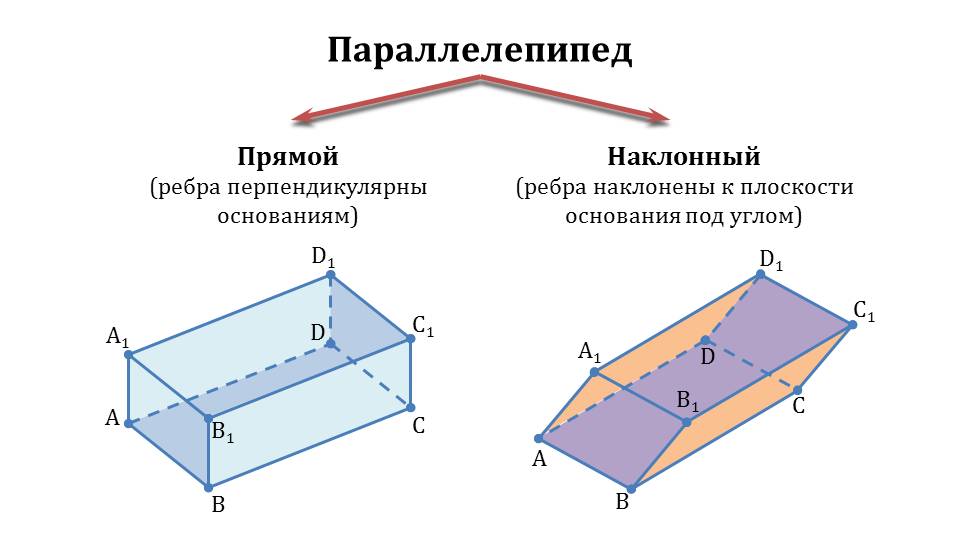
Демонстрация начинается с представления предметов, которые своей формой повторяют прямоугольный параллелепипед. На слайде представлены фото ластика, один из которого – в форме прямоугольного параллелепипеда, а второй является непрямоугольным параллелепипедом. На следующем слайде изображены геометрические тела, повторяющие форму представленных на фото ластиков – прямоугольный параллелепипед ABCDA1B1C1D1 и наклонного параллелепипеда ABCDA1B1C1D1.
К представленным параллелепипедам добавлены названия их видов – прямоугольный параллелепипед, в котором ребра перпендикулярны основаниям, и наклонный параллелепипед, в котором ребра являются наклоненными под углом к основанию. При этом отмечается, что прямоугольный параллелепипед – это прямой параллелепипед, основание которого – прямоугольник. Примерами прямоугольных параллелепипедов являются встречающиеся в жизни предметы, форма которых повторяет прямоугольный параллелепипед – системный блок компьютера, книги, микроволновая печь.
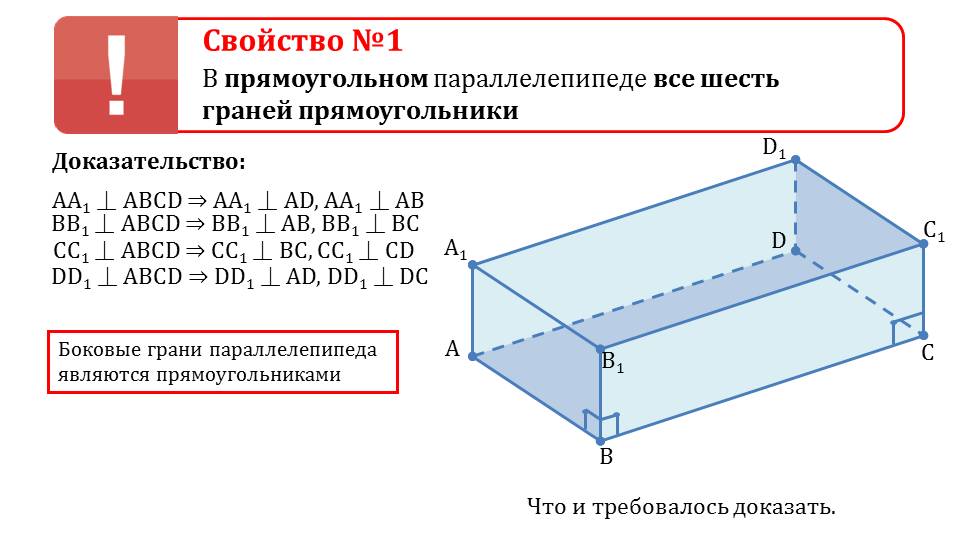
Представлено доказательство теоремы о том, что всеми шестью гранями прямоугольного параллелепипеда являются прямоугольники. Данная теорема представлена как свойство параллелепипеда. Формулировка теоремы выделена в рамку и рекомендована для запоминания. Доказательство теоремы сопровождается рисунком, на котором изображен прямоугольный параллелепипед ABCDA1B1C1D1. Перпендикулярность бокового ребра AA1 к основанию ABCD означает перпендикулярность этого ребра ребрам основания AD и AB. Перпендикулярность бокового ребра ВВ1 к основанию ABCD означает перпендикулярность ребра ребрам основания АВ и ВС. Также перпендикулярность бокового ребра СС1 к основанию ABCD означает перпендикулярность этого ребра ребрам основания СD и ВС. Аналогично доказывается перпендикулярность DD1 к ребрам основания AD и DC. Таким образом, боковые грани параллелепипеда – прямоугольники.

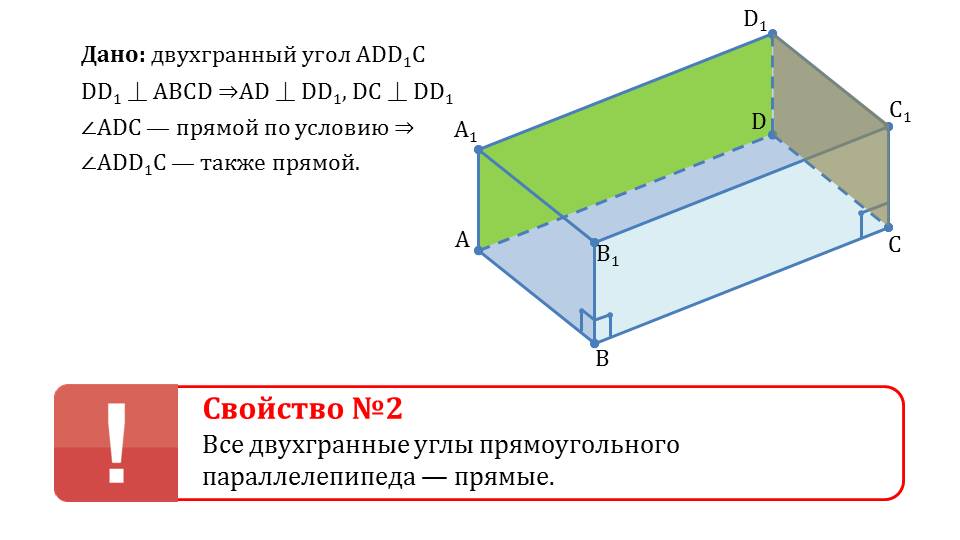
Далее представлено второе свойство, утверждающее о том, что двухгранные углы прямоугольного параллелепипеда являются прямыми. Формулировка свойства заключена в рамку и выделена для запоминания. Рядом с теоремой демонстрируется рисунок, на котором изображен прямоугольный параллелепипед ABCDA1B1C1D1. Прежде чем доказывать теорему, на примере построения описывается условие теоремы – дан двугранный угол ADD1C, боковые грани параллелепипеда перпендикулярны основанию ABCD. Угол ∠ADC является прямым по условию. Из этого следует, что угол ∠ ADD1C также является прямым. Теорема доказана.
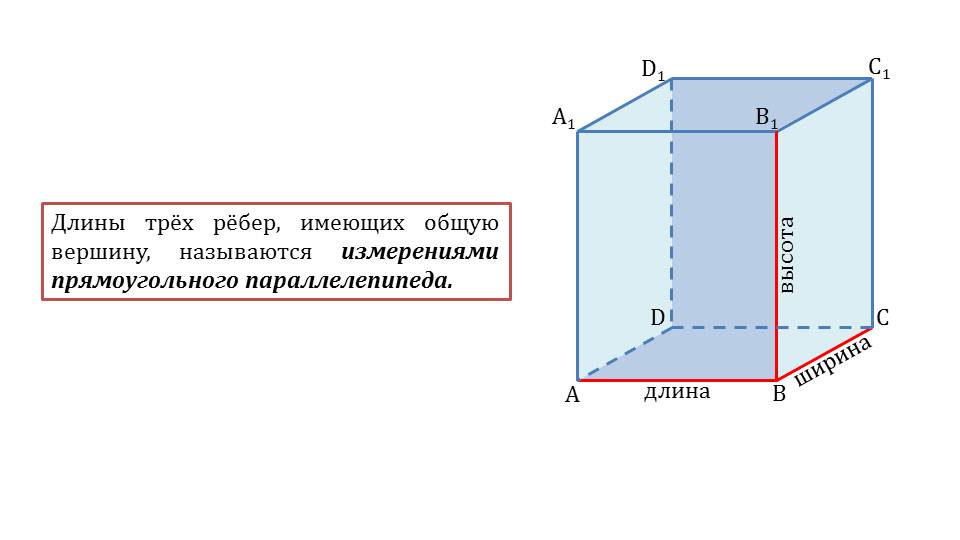
Рассматриваются элементы прямоугольного параллелепипеда. В рамке выделено определение измерений прямоугольного параллелепипеда – трех ребер с общей вершиной. Рядом с текстом определения изображен параллелепипед ABCDA1B1C1D1. На рисунке выделены красным цветом три ребра с общей вершиной – АВ, ВВ1, ВС.
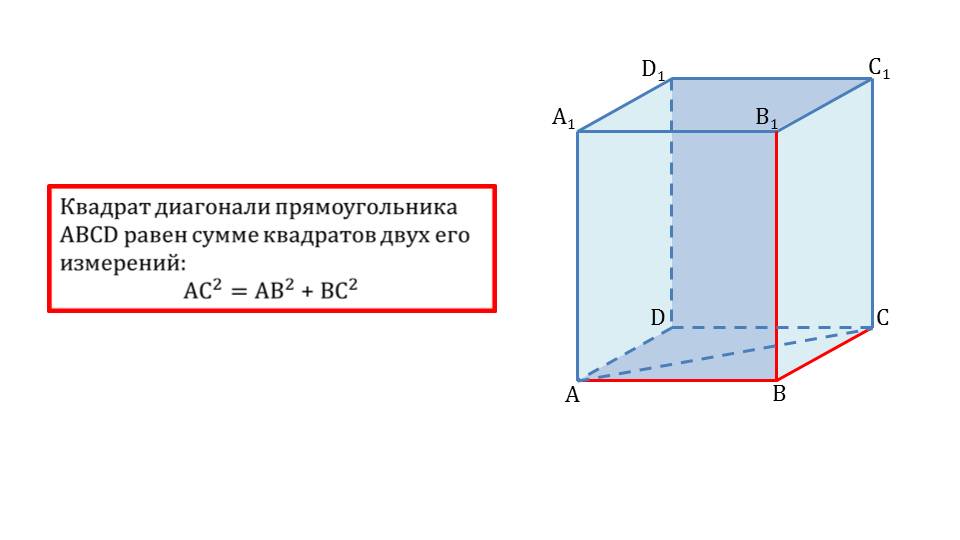
На следующем слайде ученикам напоминается, что квадрат диагонали прямоугольника ABCD вычисляется как сумма квадратов двух измерений АС2=АВ2+ВС2. Рядом со свойством изображается прямоугольный параллелепипед ABCDA1B1C1D1, в котором пунктиром отмечена диагональ АС, а также цветом выделены АВ, ВС и ВВ1.
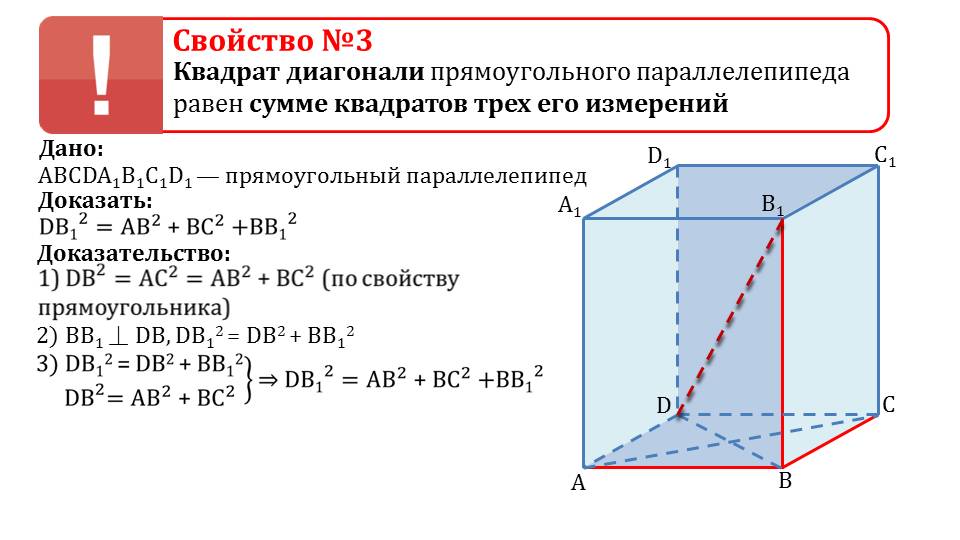
Далее представлено третье свойство прямоугольного параллелепипеда, которое свидетельствует о равенстве квадрата диагонали прямоугольного параллелепипеда сумме квадратов его трех измерений. Доказательство сопровождается изображением прямоугольного параллелепипеда ABCDA1B1C1D1., в котором проведена пунктирной линией диагональ B1D, а также проведены диагонали основания BD и АС. Необходимо доказать равенство DB12=АВ2+ВС2+ВВ12. Зная свойство прямоугольник, можно утверждать DB2= АС2=АВ2+ВС2. Отмечается перпендикулярность ребра ВВ1 и диагонали DB. Из треугольника ΔDB1B следует равенство DB12=DВ2+ ВВ12. Из установленных равенств следует и равенство квадрата диагонали параллелепипеда сумме квадратов ребер, выходящих из одной вершины, то есть DB12=АВ2+ВС2+ВВ12. Утверждение доказано.
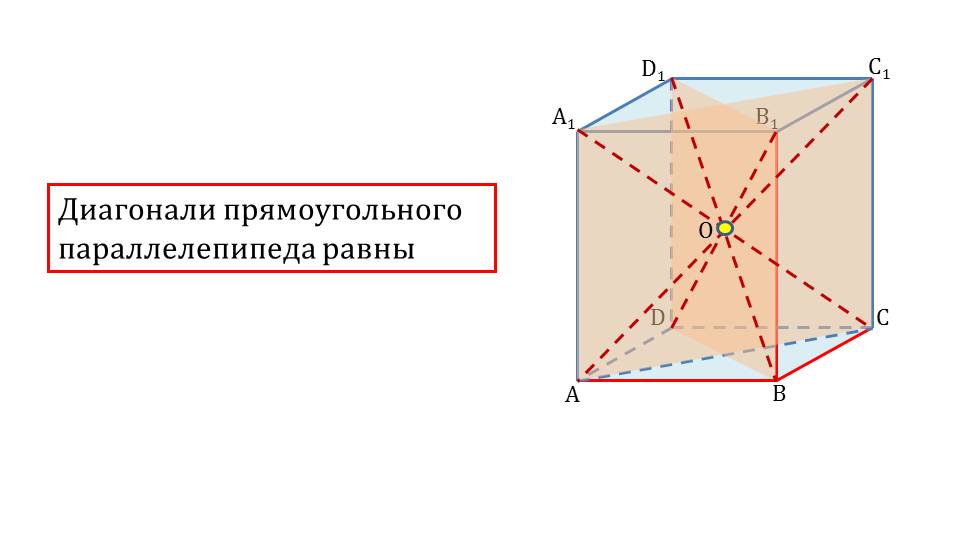
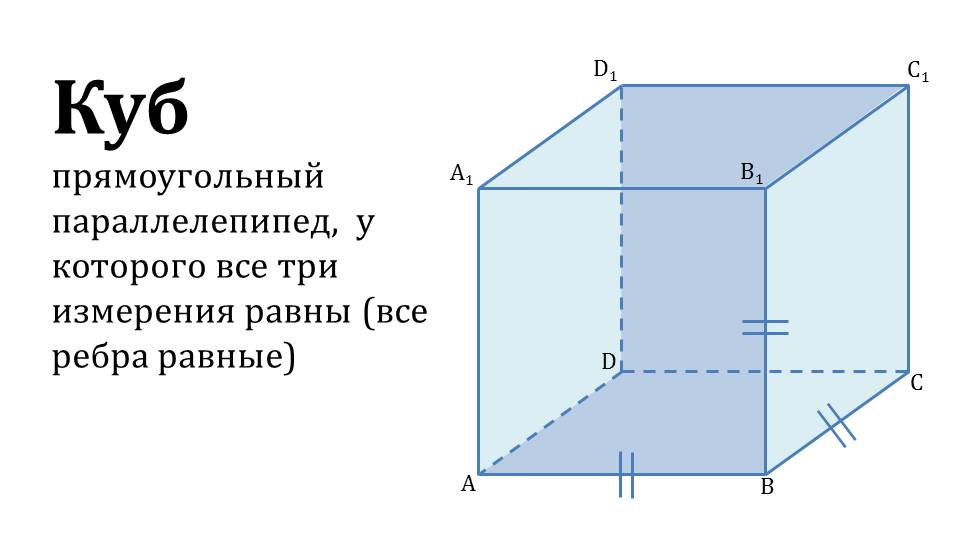
Также отмечается свойство прямоугольного параллелепипеда о равенстве всех его диагоналей. На рисунке рядом со свойством изображен параллелепипед ABCDA1B1C1D1. В параллелепипеде отмечены пунктирной линией отмечены все диагонали параллелепипеда АС1, А1С, ВD1, B1D и их точка пересечения О. На слайде 12 представлен куб ABCDA1B1C1D1, и дано его определение. На экране отображается, что куб является прямоугольным параллелепипедом с равными измерениями. На рисунке отмечены равные ребра.
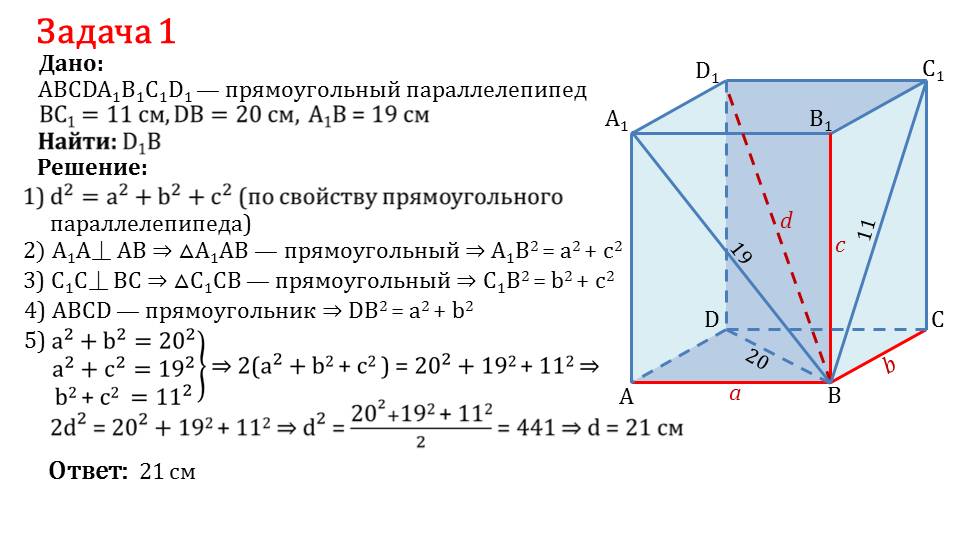
На следующем слайде представлено описание решения задачи, в которой необходимо найти длину диагонали D1B. В задаче дается прямоугольный параллелепипед ABCDA1B1C1D1., в котором диагональ грани ВС1=11 см, диагонали основания BD=20 см, а диагональ А1В=19 см. Чтобы решить задачу, нужно использовать равенство, отображающее свойство прямоугольного параллелепипеда d2=a2+b2+c2. Перпендикулярность боковых ребер АВ и А1А указывает на то, что треугольник ΔА1АВ является прямоугольным, поэтому А1В2=а2+с2. Аналогично из перпендикулярности ребер С1С и ВС следует верное для прямоугольного треугольника ΔС1СВ равенство С1В2=b2+с2. Из прямоугольника ABCD следует DВ2=b2+а2. Подставив известные значения длины ребер, получается а2+b2=202, а2+b2=192, а2+b2=112. Из равенств следует 2(а2+b2+с2)= 202+192+112. Данное выражение равно 2d2, отсюда d2=202+192+112/2=441. Длина диагонали равна 21 см.
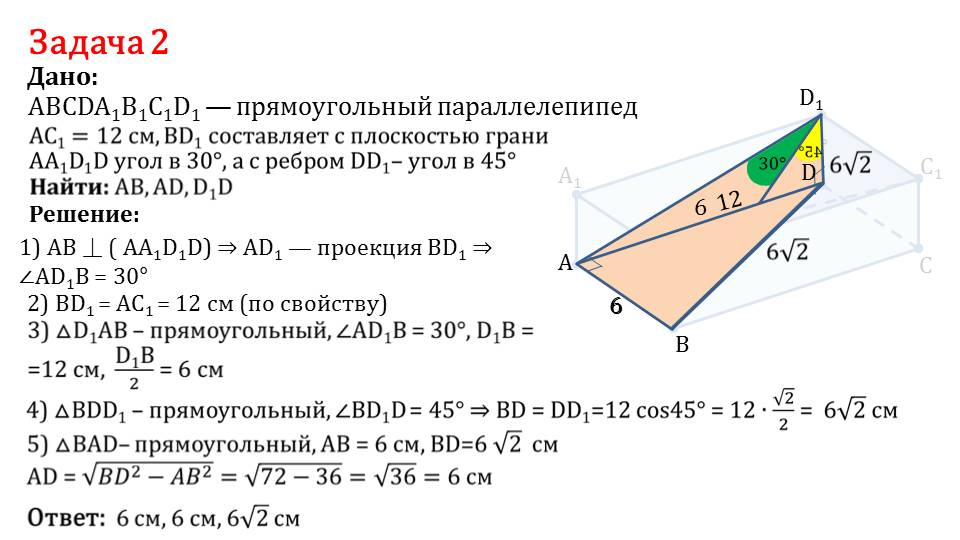
На последнем слайде демонстрируется описание решения задачи, в которой необходимо найти измерения параллелепипеда ABCDA1B1C1D1 – длину ребер АВ, AD, D1D. При том, что дана длина диагонали параллелепипеда АС1=12 см. Угол между диагональю BD1 и гранью АА1D1D составляет 30°, а угол между диагональю BD1 и ребром D1D равен 45°. Из свойства параллелепипеда следует BD1=АC1=12 см. Так как треугольник ΔD1AB прямоугольный, то угол ∠AD1B=30°, а его стороны BD1=12 см, то есть BD1/2=6 см. Так как треугольник ΔВD1D прямоугольный, его ∠ВD1D=45°. Учитывая это, можно найти BD=DD1=12cos45°=12·√/2=6√2. Для прямоугольного треугольника ΔВАD со сторонами АВ=6 см и BD=6√2 см следует AD=√(BD2-AB2)= 6 см. Задача решена.
Презентация «Прямоугольный параллелепипед» предназначена для повышения эффективности традиционного урока геометрии в школе. Также данный материал успешно может использоваться в ходе дистанционного обучения. Пособие может быть рекомендовано ученикам, которые недостаточно хорошо освоили тему или изучают ее самостоятельно.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 12082 |
| Номер материала | 896 |