
Презентация "Расстояние от точки до плоскости"

Краткое описание документа:
Презентация «Расстояние от точки до плоскости» детально рассматривает понятие расстояния от точки до плоскости, формирует умение использовать знания о расстояния между точками при решении геометрических задач. В ходе презентации с помощью анимации производятся построения, раскрывающие смысл понятия расстояния между точкой и плоскостью, дается определение перпендикуляра и наклонной, проведенных от точки до плоскости, проекции наклонной и расстояния от точки до плоскости, несколько важных утверждений по теме, пример решения задачи.
В презентации широко используются анимационные эффекты, с помощью которых учитель может продемонстрировать отличия понятий перпендикуляра, наклонной, проекции. Такой способ подачи учебного материала очень эффективный и ускоряет достижение целей обучения. Определения, которые требуют запоминания, выделены в рамку и цветом. Такое выделение помогает лучше запомнить информацию, лучше ее усвоить.
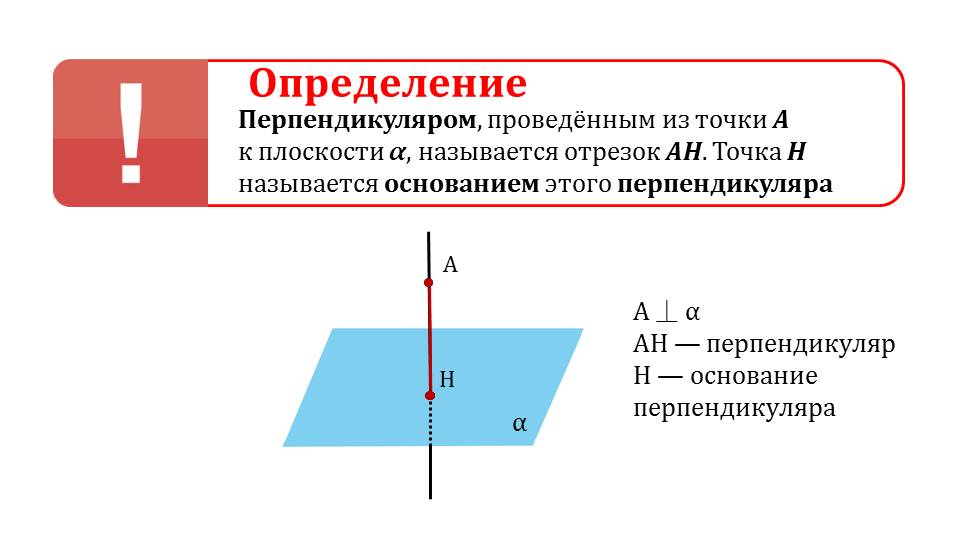
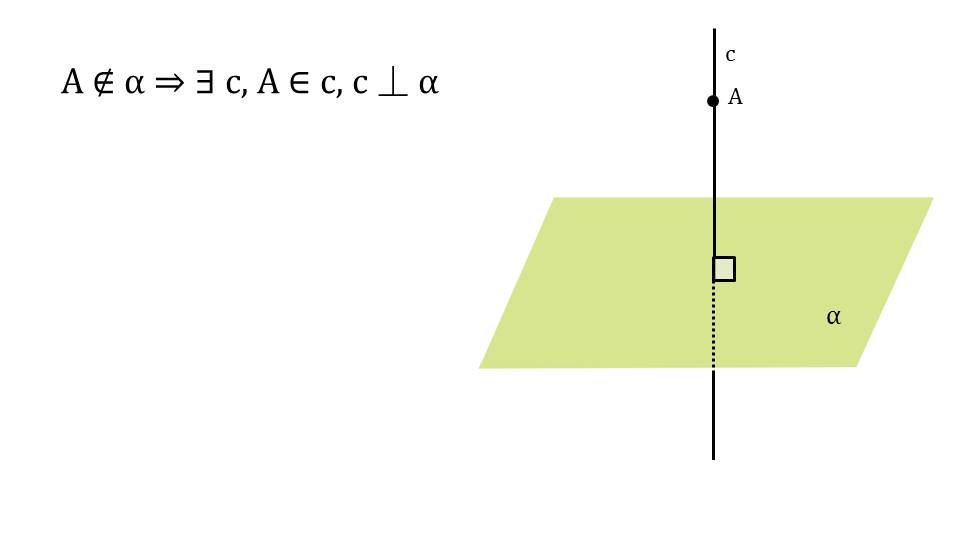
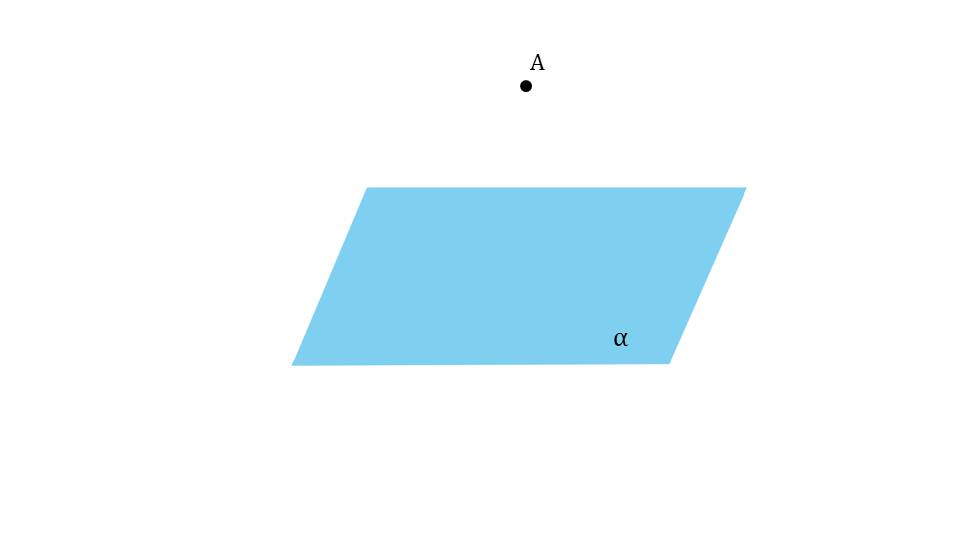
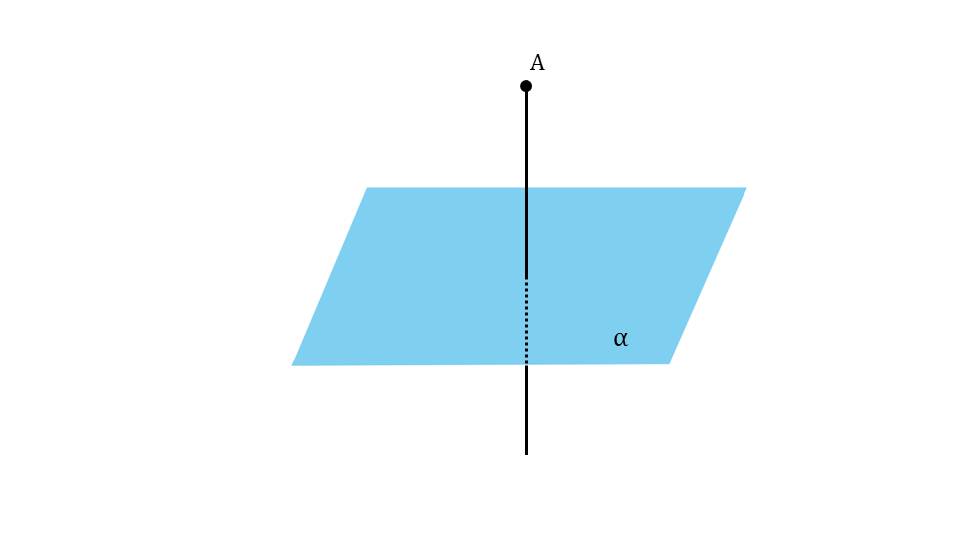
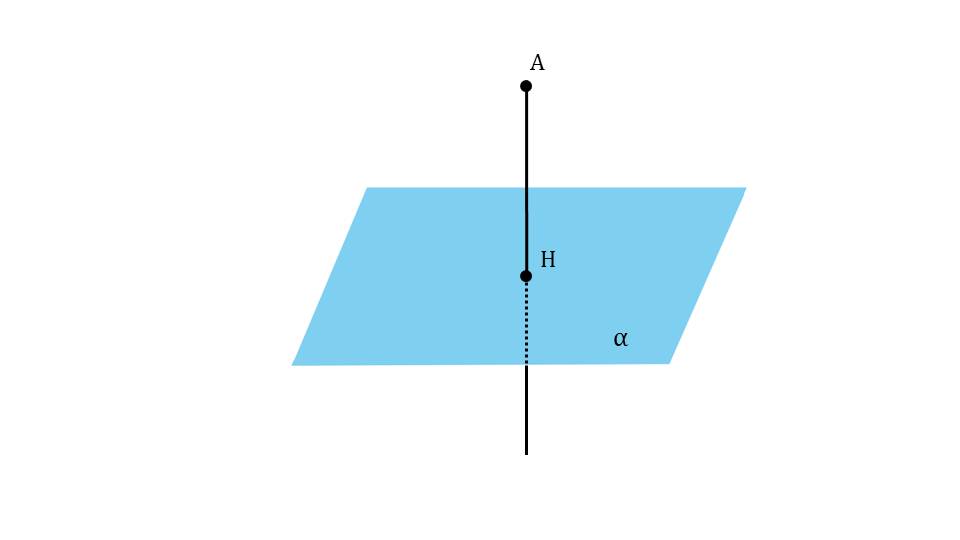
Презентация начинается с построения изображения плоскости α, закрашенной зеленым цветом, и некоторой точки А, не принадлежащей ей. Через точку А проводится прямая с, перпендикулярная плоскости α. На рисунке обозначено, что между плоскостью и прямой с образуется угол 90°. Далее на рисунке изображается еще плоскость α, закрашенная синим цветом, не принадлежащая ей точка А и прямая, пересекающаяся с плоскостью в точке Н, выделяя полученный таким образом отрезок АН. Таким образом вводится понятие перпендикуляра, проведенного из точки А к плоскости, который представляет собой отрезок АН с основанием в точке Н. данное определение отображено на отдельном слайде и выделено в рамке. на рисунке отдельно указаны элементы построения перпендикуляра к плоскости – сам перпендикуляр, основание, а также обозначение А┴а.
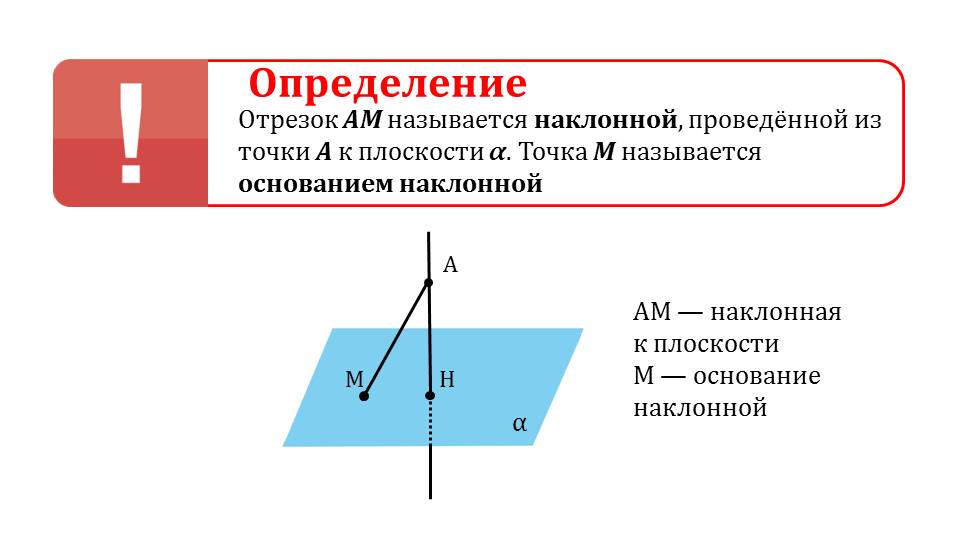
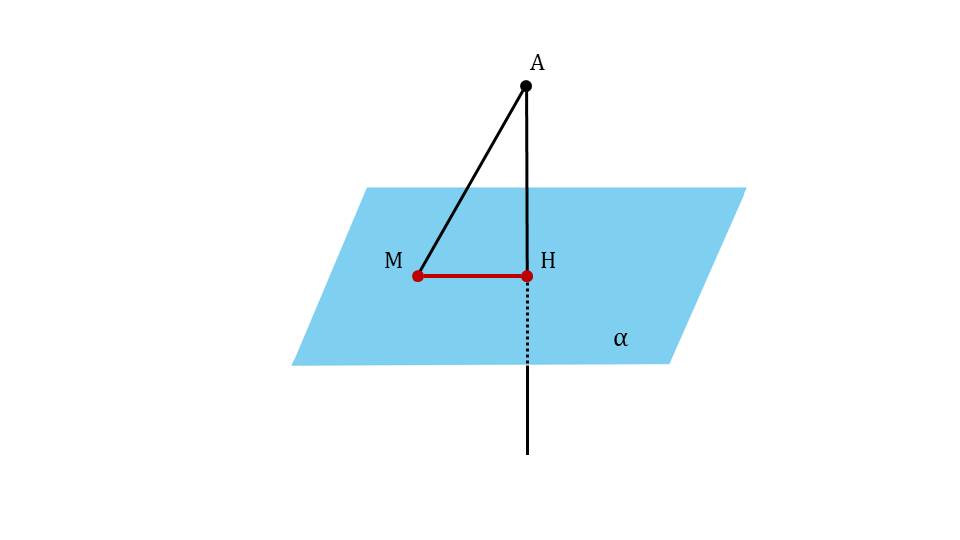
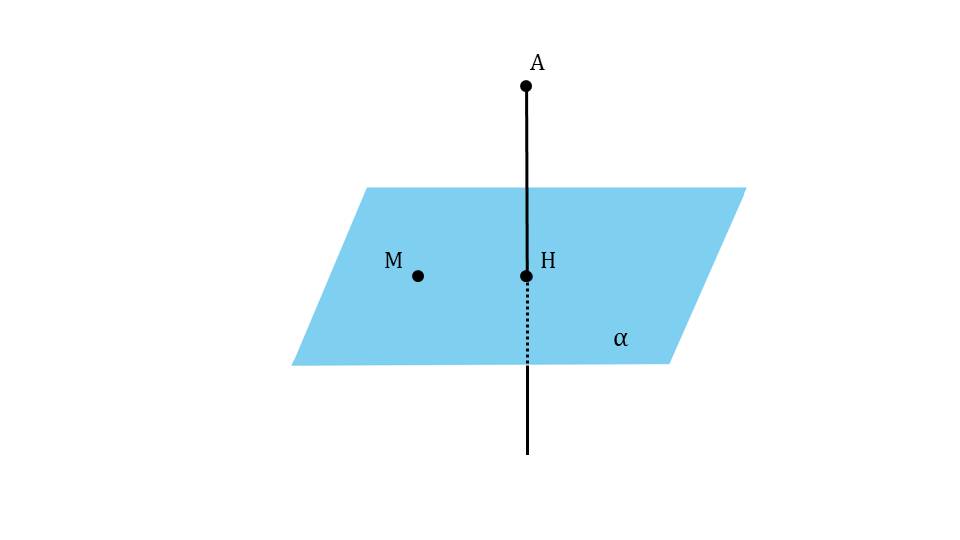
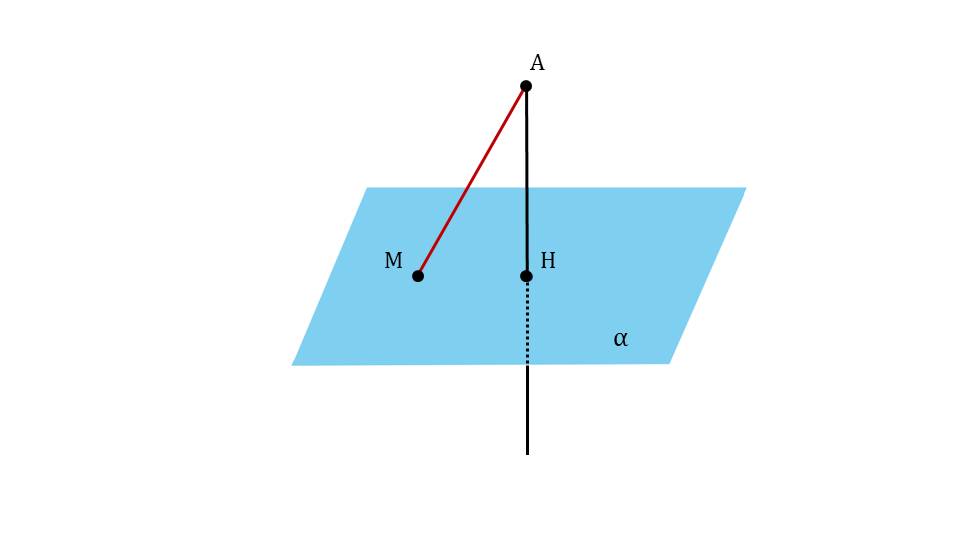
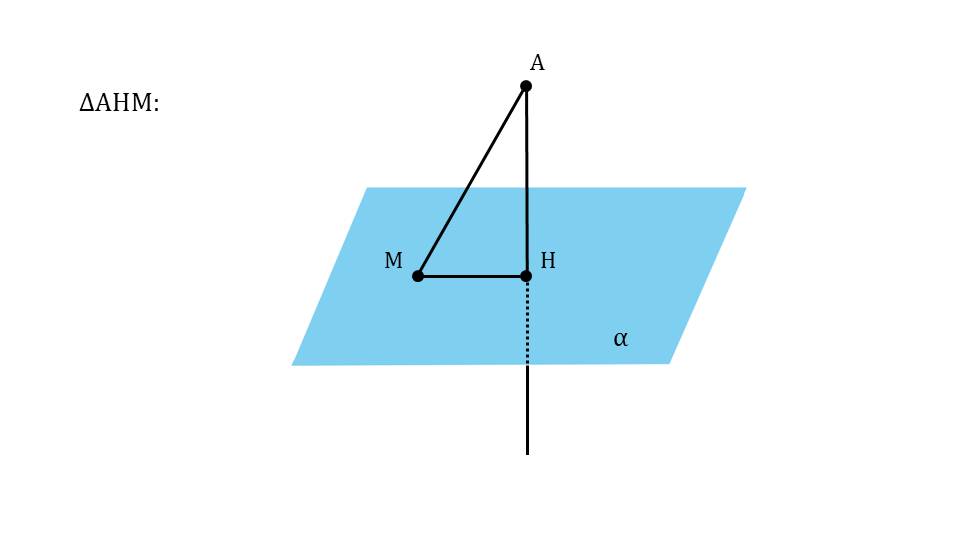
На следующем слайде к продемонстрированному рисунку плоскости и проведенного к ней перпендикуляра АН добавляется точка М, не принадлежащая перпендикуляру, но лежащая на плоскости α. От точки А к М проводится отрезок АМ, выделенный цветом. Таким образом вводится понятие наклонной, определение которой дано на следующем слайде. Там указано, что АМ является наклонной, проведенной из А к плоскости α с основанием в точке М. Под определением указаны названия введенных понятий – наклонной и основания наклонной.
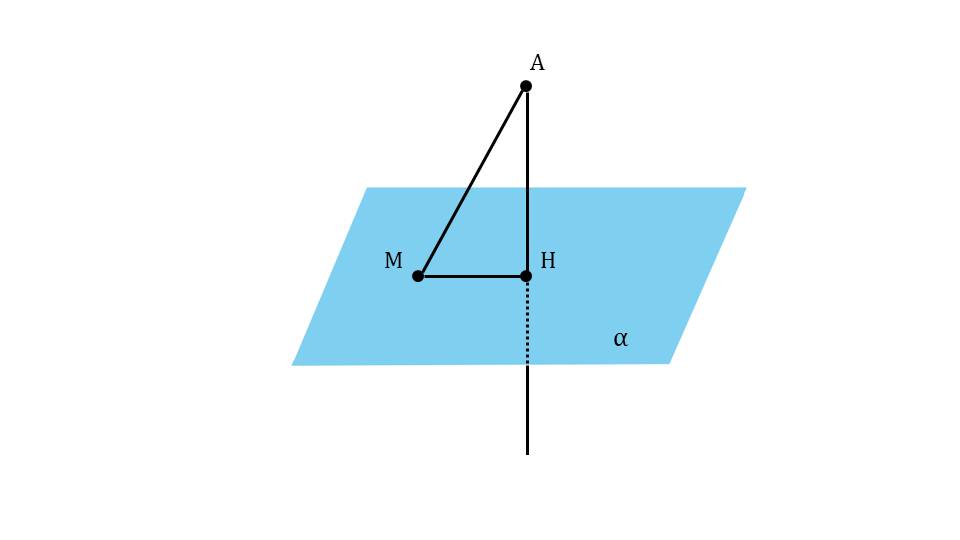
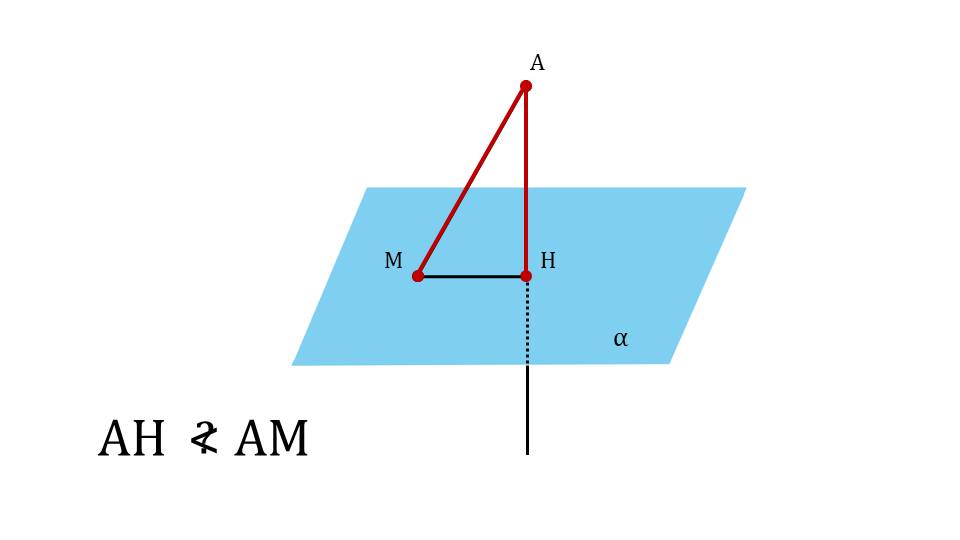
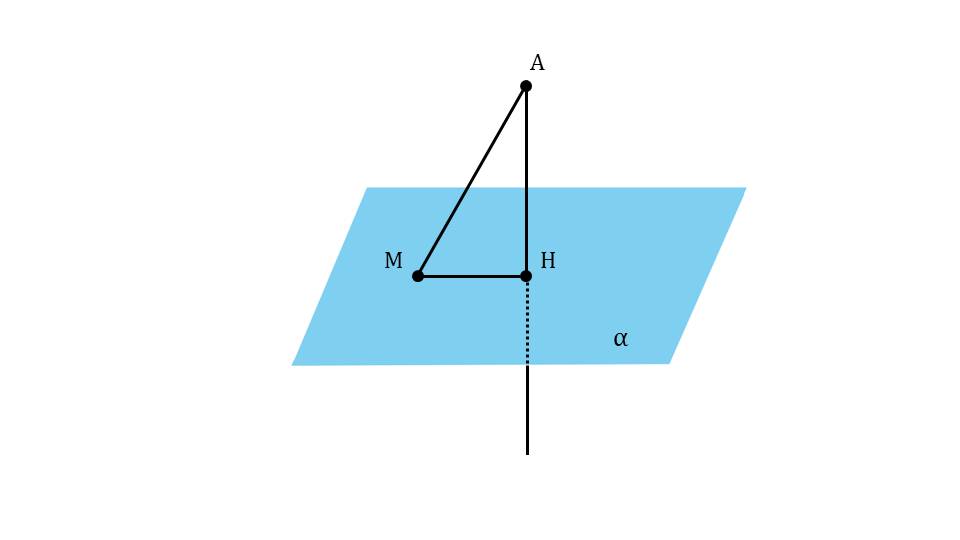
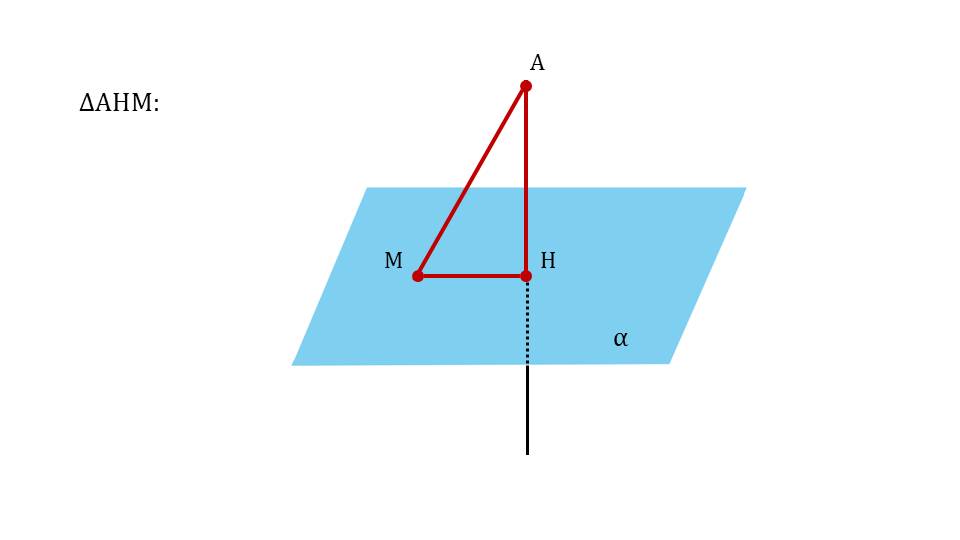
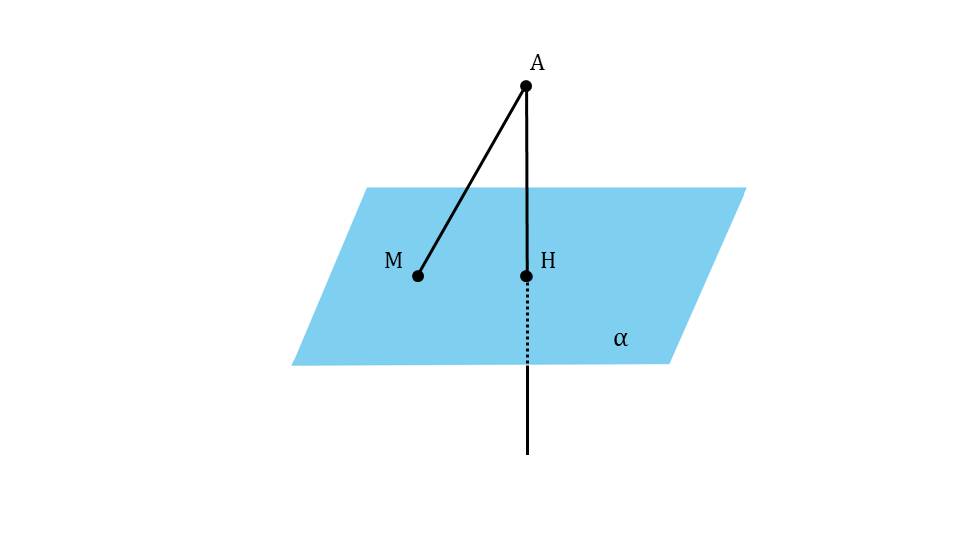
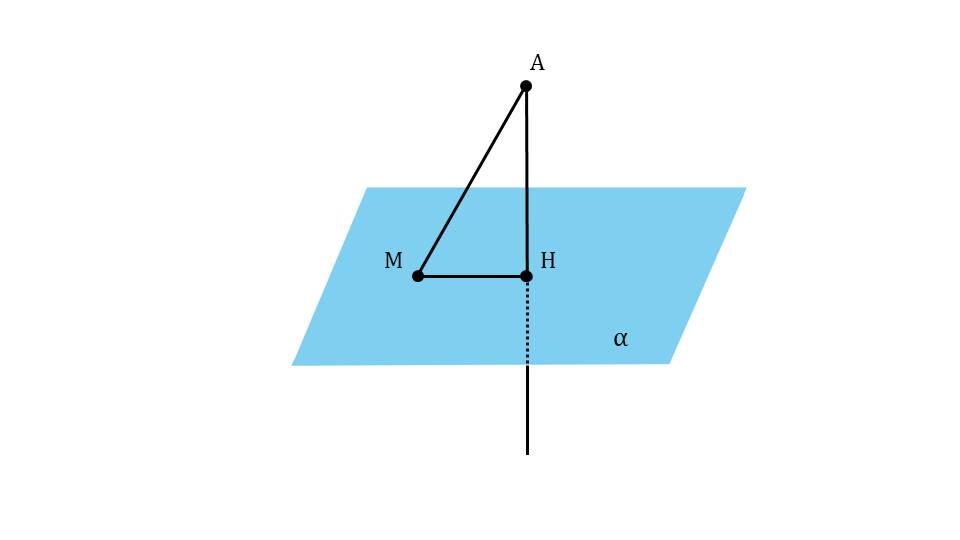
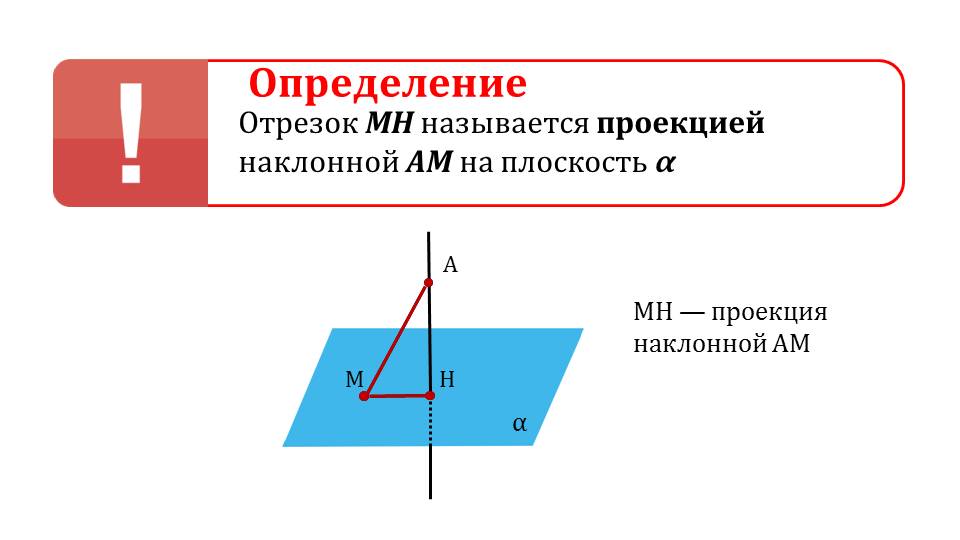
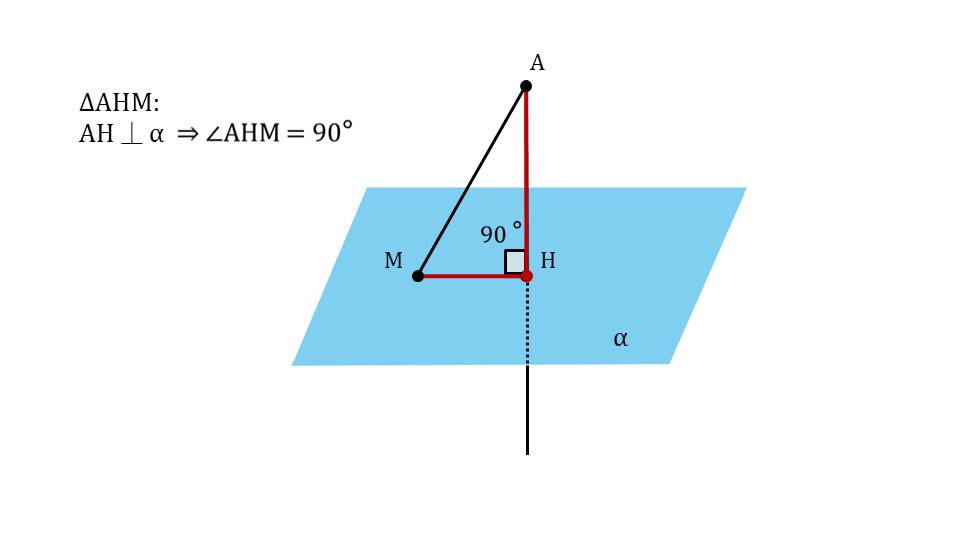
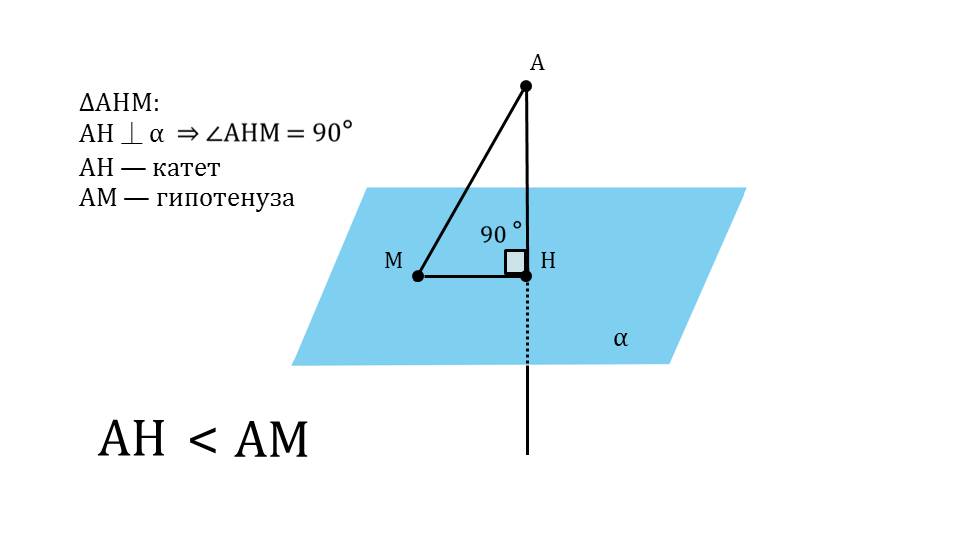
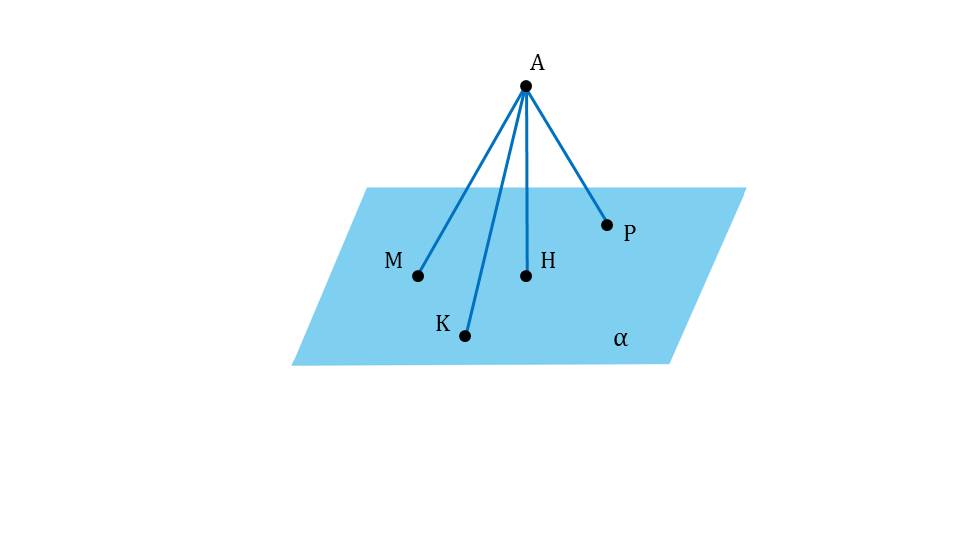
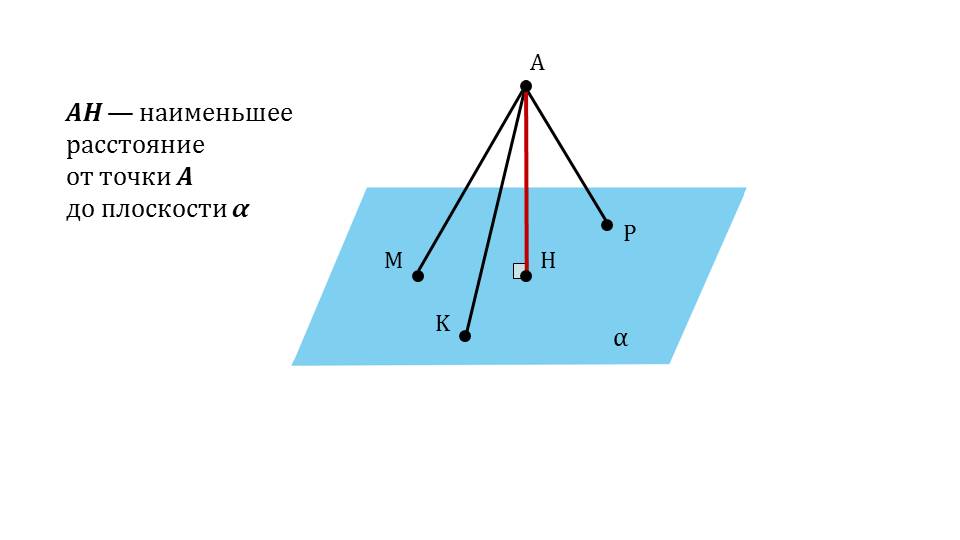
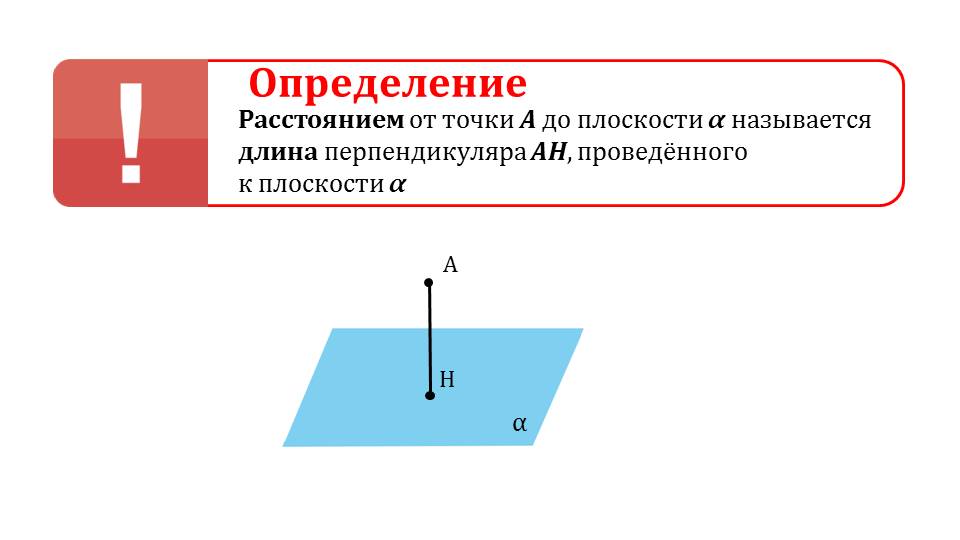
На следующем слайде рисунок дополняется отрезком МН, выделенным красным цветом. Это проекция, которая на слайде 13 определяется как результат построения на данном рисунке – отрезок МН. Под определением демонстрируется сделанный рисунок и указано проекция МН наклонной АМ. Далее с помощью анимации ставится вопрос о том, является ли перпендикуляр меньшим отрезком, чем наклонная. Ответ на этот вопрос можно получить, рассматривая треугольник ΔАНМ. Обращается внимание на величину угла ∠АНМ=90°. То есть треугольник является прямоугольным, а в прямоугольном треугольнике катет всегда меньше гипотенузы, поэтому на экране отображается вывод АН<АМ. Демонстрируется построение множества наклонных, опущенных из точки А на плоскость – АМ, АК, АР. Однако при этом перпендикуляр АН представляет наименьшее расстояние от точки А до плоскости α. Далее демонстрируется текст определения расстояния от точки А до плоскости α на основе сделанного построения как длины перпендикуляра АН.
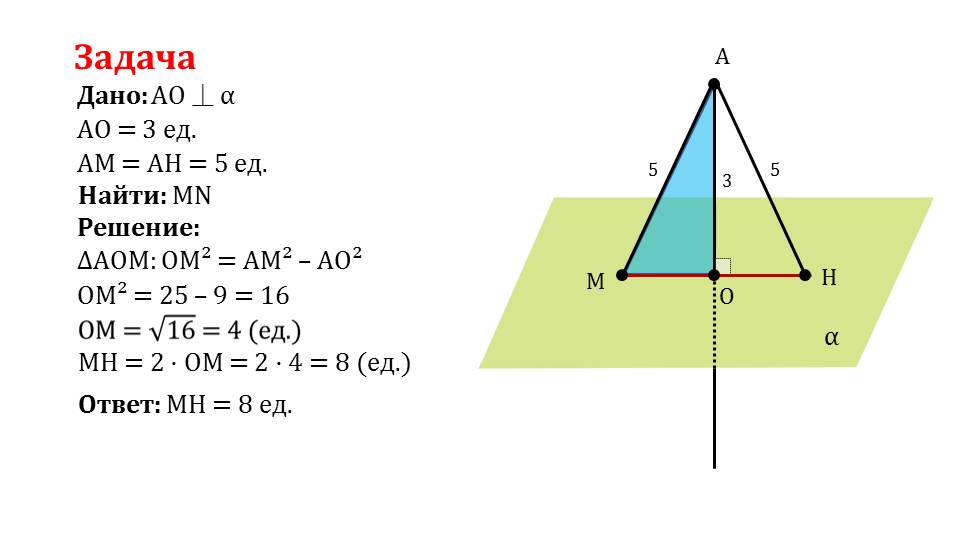
Описывается решение задачи, в которой дана плоскость α и проведенный к ней перпендикуляр АО., составляющий 3 единицы, при этом наклонные АМ и АН равны 5 единицам. Необходимо найти расстояние между основаниями наклонной – длину МН. При решении задания напоминается правило для треугольника ΔАОМ – ОМ2=АМ2-АО2. Подставляя известные по условию значения, получаем ОМ=√(25-9)=4. Так как МН=2·ОМ, то МН=8 единиц.
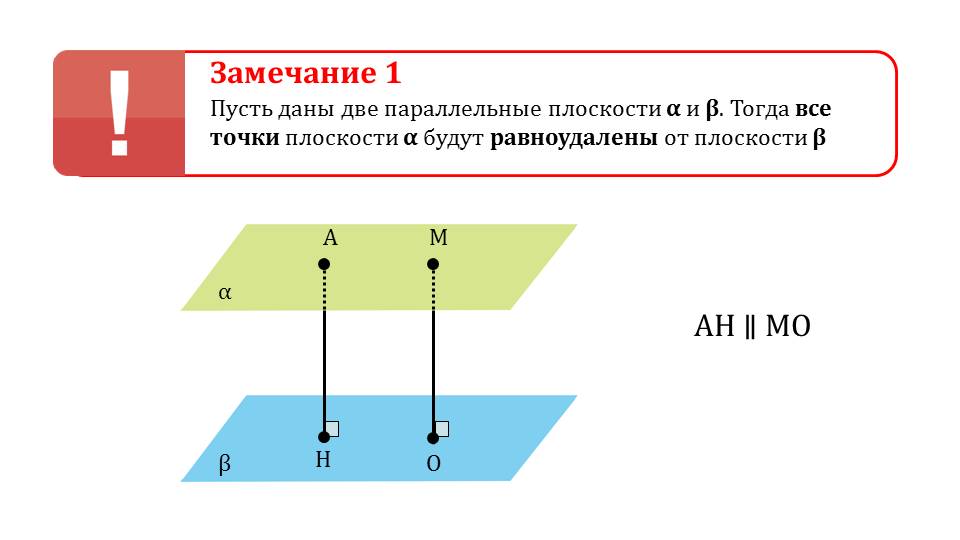
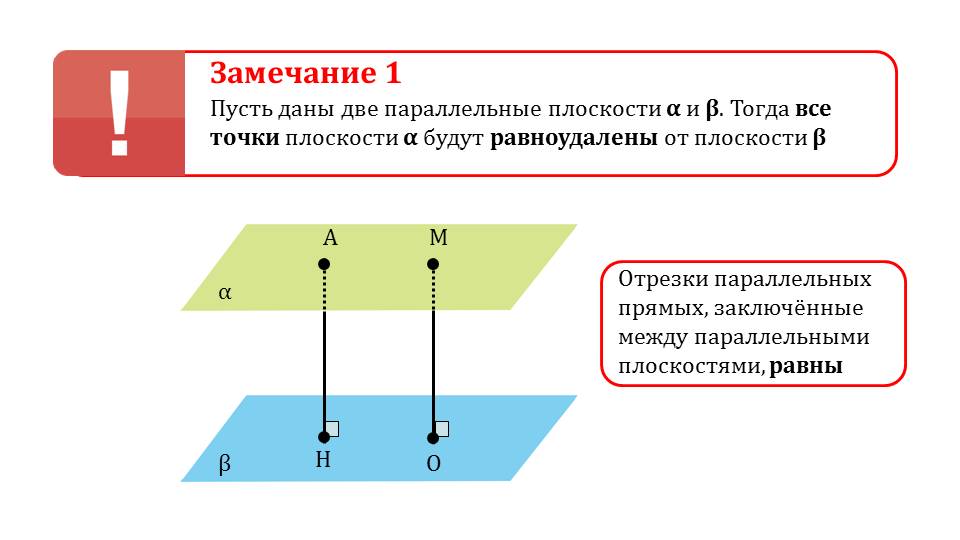
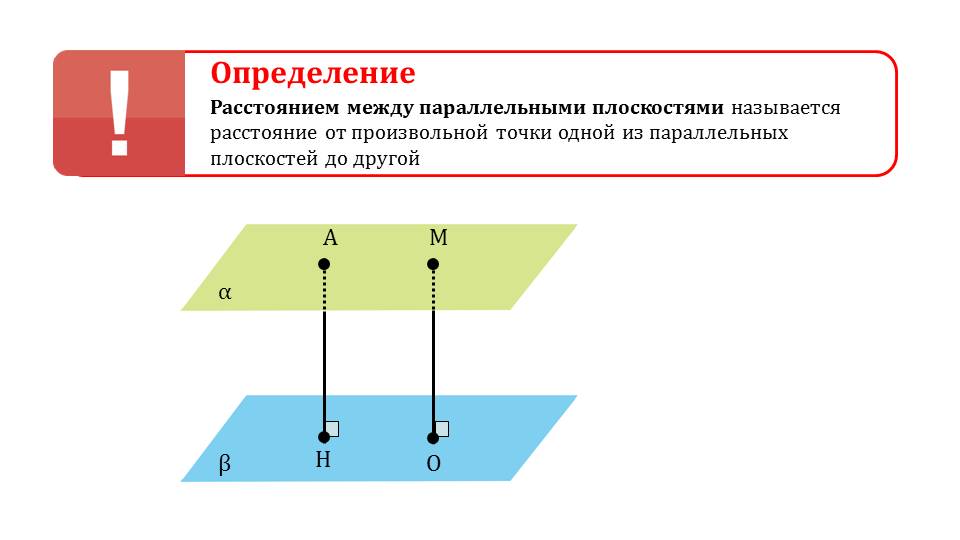
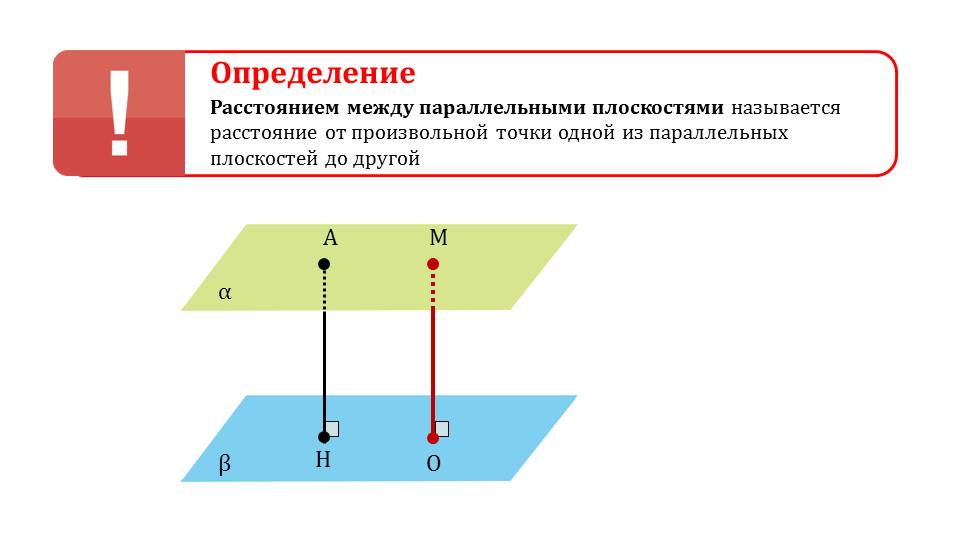
На следующем слайде делается замечание о свойствах расстояния между параллельными плоскостями – они являются равноудаленными друг от друга, к тому же перпендикуляры параллельны между собой. Также указывается на равенство параллельных отрезков, заключенных между плоскостями. Дается определение расстояния между параллельными плоскостями как расстояния между произвольными точками одной и другой, учитывая перпендикулярность полученного отрезка к обеим плоскостям.
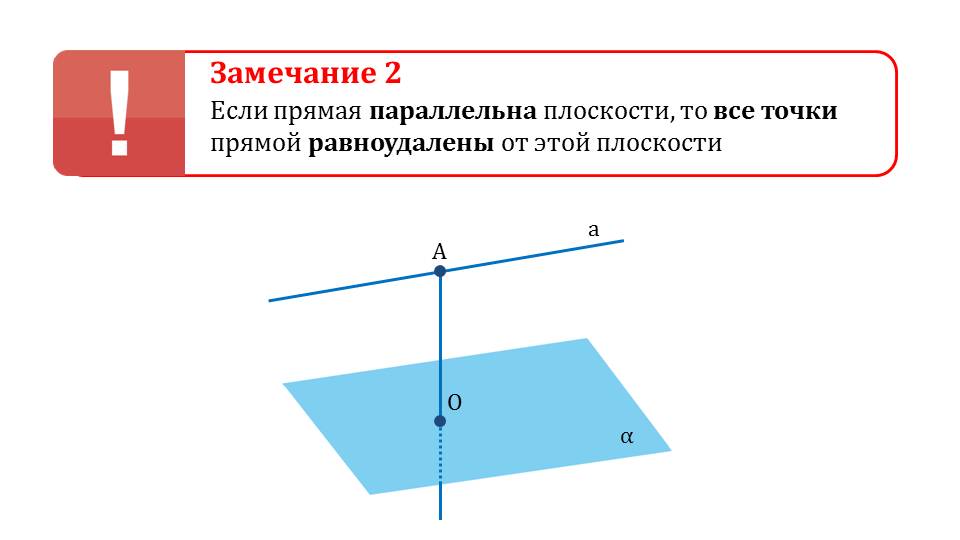
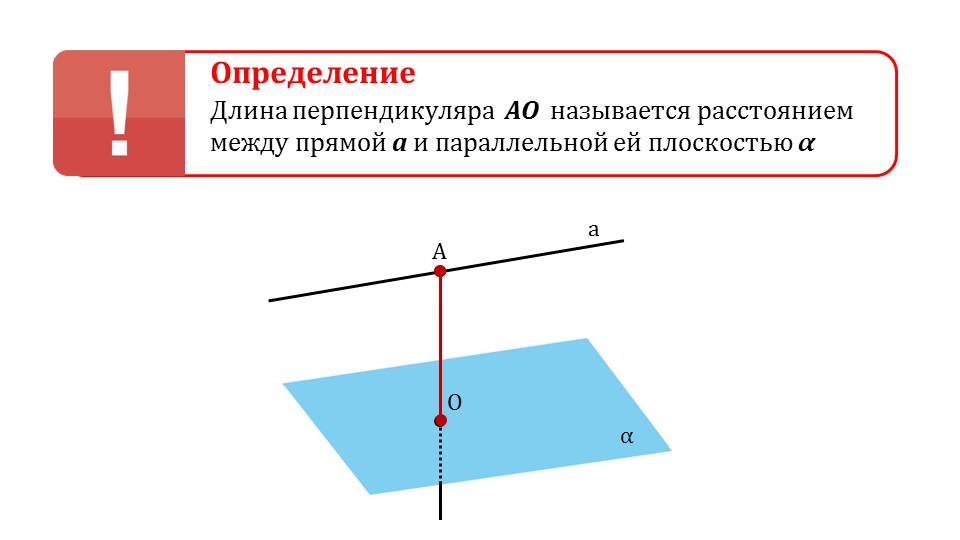
Далее указано замечание о свойствах расстояния между плоскостью и параллельной ей прямой – отмечается равноудаленность всех точек этой прямой до плоскости. Далее продемонстрировано определение расстояния между прямой и параллельной плоскостью α как длина перпендикуляра АО. Определение сопровождается рисунком, на котором изображена плоскость α, параллельная прямая а и перпендикуляр, проведенный из точки А, принадлежащей прямой, к плоскости.
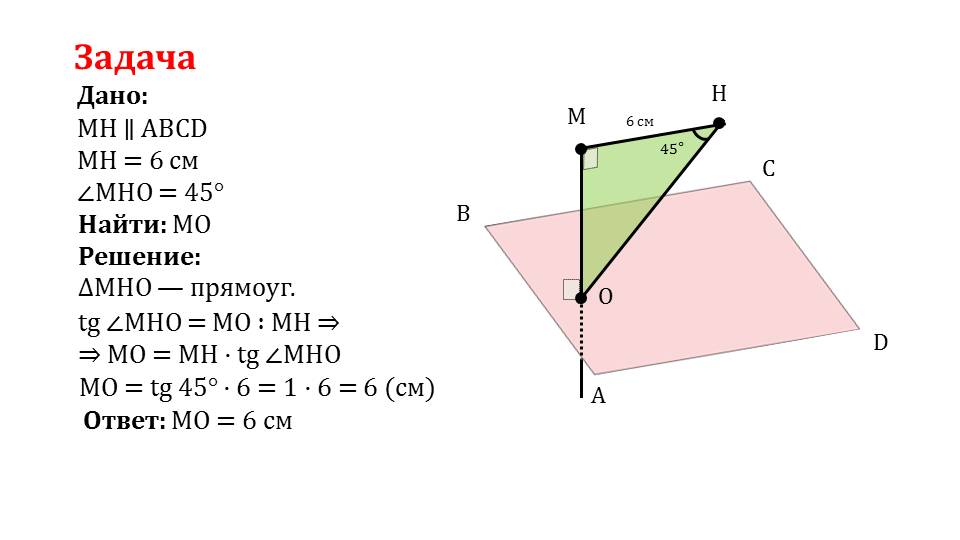
В качестве примера приводится описание решения задачи, в которой дана плоскость ABCD, отрезок МН=6 см, расположенный паралельно плоскости. Из М опущен перпендикуляр на плоскость с основаним в точке О. При этом угол ∠МНО=45°. Нужно найти расстояние от М до О. При решении задачи рассматривается образованный при построении треугольник ОМН. Это прямоугольный треугольник, поэтому tg∠МНО=МО/МН. Отсюда МО= МН· tg∠МНО, то есть МО= tg 45°·6=6 см.
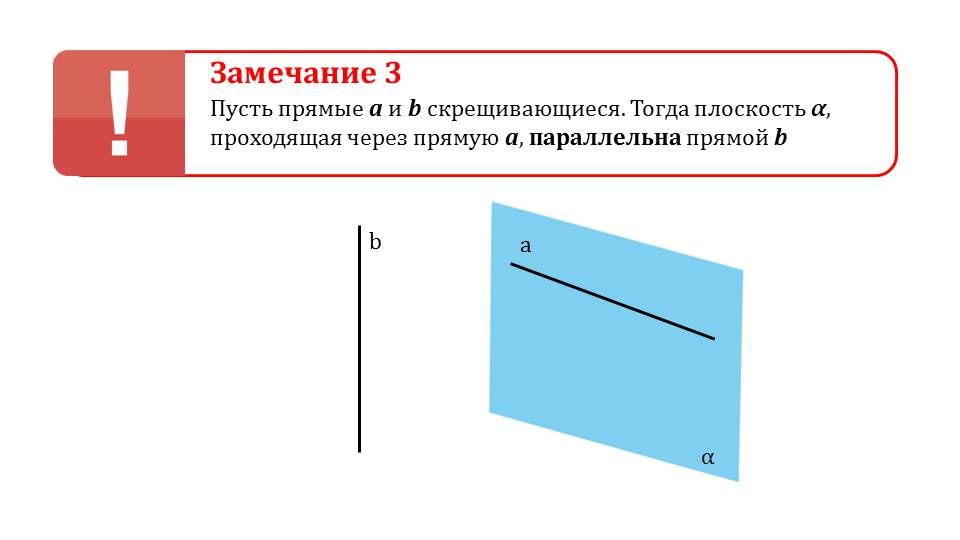
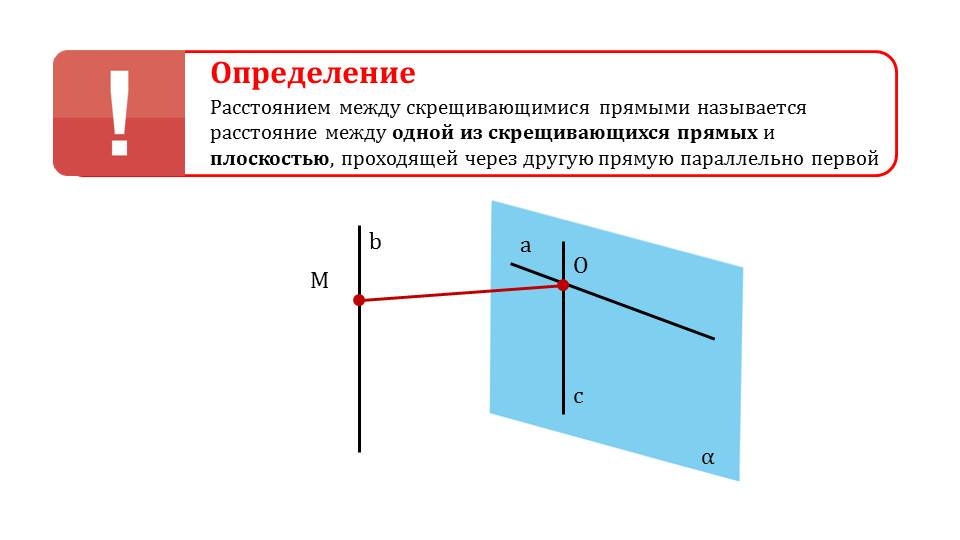
К данной теме дается еще одно важное замечание, указывающее на то, что если одна из скрещивающихся прямых лежит на плоскости, то вторая прямая параллельна этой плоскости. Также представлено определение расстояния между скрещивающимися прямыми, равного расстоянию между одной прямой и плоскостью, в которой лежит вторая прямая.
Презентация «Расстояние от точки до плоскости» может применяться учителем как средство повышения эффективности традиционного урока геометрии, используя наглядный материал. Также презентация может стать инструментом учителя, осуществляющего дистанционное обучение. При необходимости ученику освоить тему самостоятельно или углубить понимание предмета, материал может быть рекомендован для самостоятельной работы.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 7777 |
| Номер материала | 891 |