
Презентация "Разложение вектора по трём некомпланарным векторам"

Краткое описание документа:
Презентация «Разложение вектора по трём некомпланарным векторам» предназначена для обеспечения наглядности учебного материала при объяснении данной темы. Во время демонстрации ученики знакомятся с правилом разложения вектора по трем некомпланарным векторам и его доказательством, рассматривается описание решения задачи с использованием изученного материала. С помощью наглядного пособия учитель может сформировать у учеников представление о методе разложения вектора по некомпланарным векторам.

Презентация является одним из способов не только донесения учебной информации, но и удержания внимания учеников на изучении предмета. В данной презентации используются приемы выделения понятий и формул для лучшего запоминания. Также при построении объектов и структурировании подаваемой информации применяются анимационные эффекты. Эти эффекты помогают ученику освоить материал, более глубоко понять метод разложения вектора.

Демонстрация начинается с представления теоретических основ разложения вектора по векторам. В рамке выделено правило о том, что если для некоторых чисел x, y, z верно выражение p¯=xa¯+yb¯+zc¯, это означает разложение вектора p¯ по векторам a¯, b¯ и c¯. При этом числа x, y, z являются коэффициентами разложения. Подкреплением данной формулы служит теорема о разложении вектора по трем некомпланарным векторам. Теорема утверждает о том, что всякий вектор может быть разложен по трем некомпланарным векторам, а коэффициенты разложения при этом являются единственными. Теорема заключена в рамку, выделена цветом и рекомендована для запоминания ученикам. Доказательство теоремы сопровождается рисунком, на котором изображена плоскость с отмеченными на ней некомпланарными векторами a¯, b¯, c¯ и суммарным вектором p¯. Нам необходимо доказать, что p¯=xa¯+yb¯+zc¯, а также что коэффициенты разложения являются единственными. На рисунке строятся вектора, параллельные данным векторам так, что ОС¯║РР1¯, Р1Р2¯║ОВ¯, чтобы воспользоваться правилом параллелепипеда для результирующего вектора р¯. На основе построения, пользуясь правилом параллелепипеда, отмечаем ОР¯=ОР2¯+Р2Р1¯+Р1Р¯. Чтобы векторы получились нужной длины, необходимо умножать их на определенный коэффициент ОР2¯=х·ОА¯, Р1Р2¯=у·ОВ¯, Р1Р2¯=z·ОС¯. Подставляя полученные выражения в правило параллелепипеда, получаем p¯=xa¯+yb¯+zc¯. Первая часть утверждения доказана.

Доказательство второй части утверждения выполняется методом от противного. Для этого предполагаем существование еще одних коэффициентов разложения, которые составят выражение p¯=x1a¯+y1b¯+z1c¯. Разность основного и данного равенств даст выражение (x-x1)·a¯+(y-y1)·b¯+(z-z1)·c¯=0. Так как данные векторы ненулевые, то коэффициенты при них для выполнения равенства должны быть нулевыми, то есть x-x1=0, y-y1=0, z-z1=0. Неравенство нулю одной их разностей вектора, на которые раскладывается вектор, означает, что векторы являются компланарными. Следовательно, коэффициенты являются единственными для данного разложения.

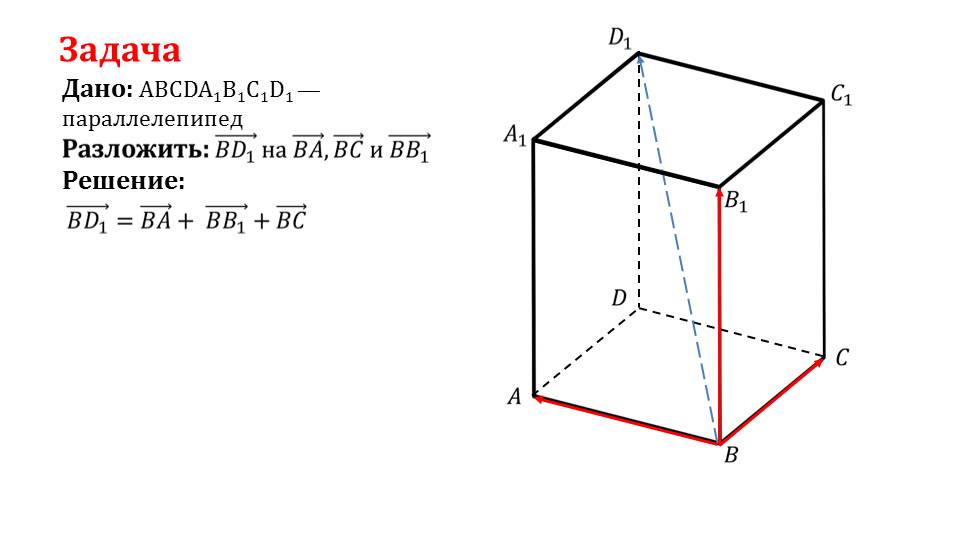
На пятом слайде предлагается рассмотреть решение задачи, в которой дан параллелепипед ABCDA1 B1C1D1, в котором необходимо разложить вектор BD1¯ по векторам ВА¯, ВС¯ и ВВ1¯. Решением данной задачи в параллелепипеде является разложение диагонали по трем измерениям, в результате чего диагональ равна сумме трех измерений BD1¯= ВА¯+ВС¯+ ВВ1¯. Решение задачи сопровождается рисунком, на котором изображен параллелепипед ABCDA1B1C1D1, выделены красным цветом три измерения параллелепипеда, выходящие из вершины В, а также суммарный вектор BD1¯.
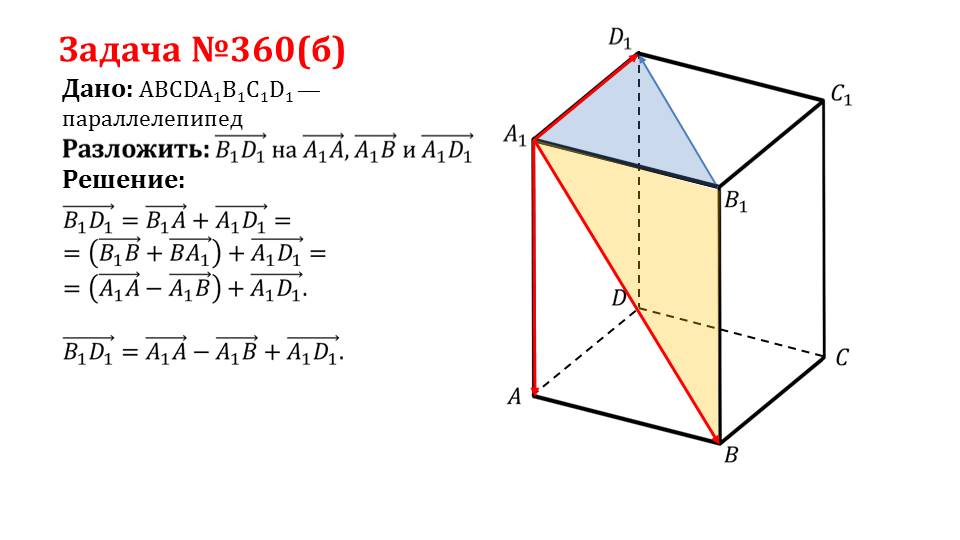
Последний слайд демонстрирует решение задачи 360(б), в которой дан параллелепипед ABCDA1B1C1D1, где требуется заложить вектор B1D1¯ на векторы А1А¯, А1В¯, A1D1¯. На рисунке изображен данный параллелепипед, на нем отмечены вектора, на которые нужно разложить вектор B1D1¯. Зная, что вектор B1D1¯ представляет собой сумму векторов В1А¯ и A1D1¯, подставляем в эту сумму выражение, в результате которого получается В1А¯= А1А¯-А1В¯. В итоге получаем искомое разложение для вектора B1D1¯= А1А¯-А1В¯+ A1D1¯.
Презентация «Разложение вектора по трём некомпланарным векторам» применяется на традиционном школьном уроке математики для повышения эффективности урока. Также данное пособие поможет донести информацию ученикам при дистанционном обучении. Презентация может быть полезной ученикам, самостоятельно осваивающим предмет или требующим дополнительного объяснения по теме.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 9660 |
| Номер материала | 914 |