
Презентация «Свойства функции»

Краткое описание документа:
Презентация «Свойства функции» представляет собой наглядное пособие для представления учителем на уроке данной темы. При помощи анимации и других инструментов данной формы представления материала предоставляется возможность наглядной демонстрации свойств функции и порядка их определения для некоторой функциональной зависимости.

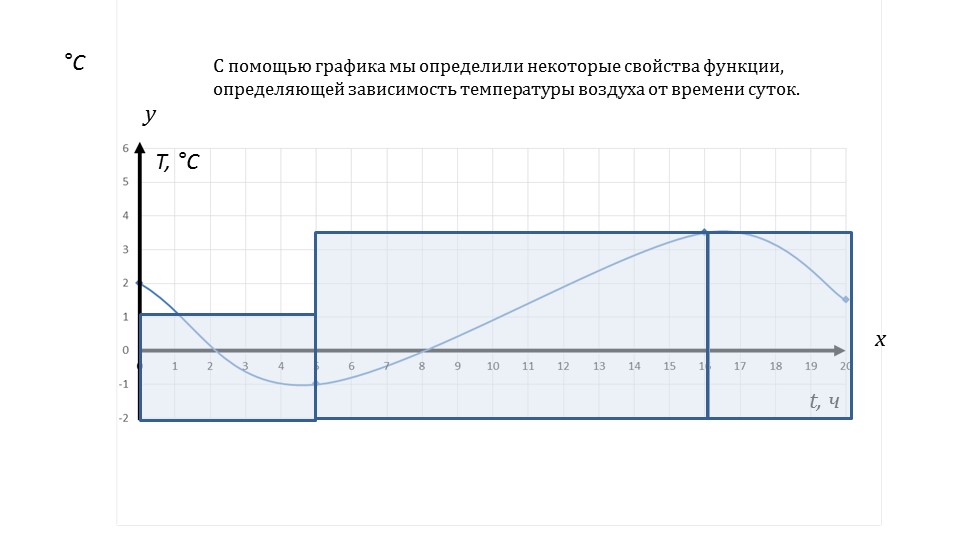
На первом слайде демонстрируется график зависимости температуры окружающего воздуха от времени в течение 20 часов. График представляет собой кривую линию с участками возрастания и снижения по оси ординат. На графике видно, что температура воздуха с 0 до 5 часов постепенно снижается, с 5 утра 16 часов постепенно возрастает, а с 16 часов до 20 –снова снижается. Периоды возрастания и уменьшения значений функции являются важной характеристикой функциональной зависимости.

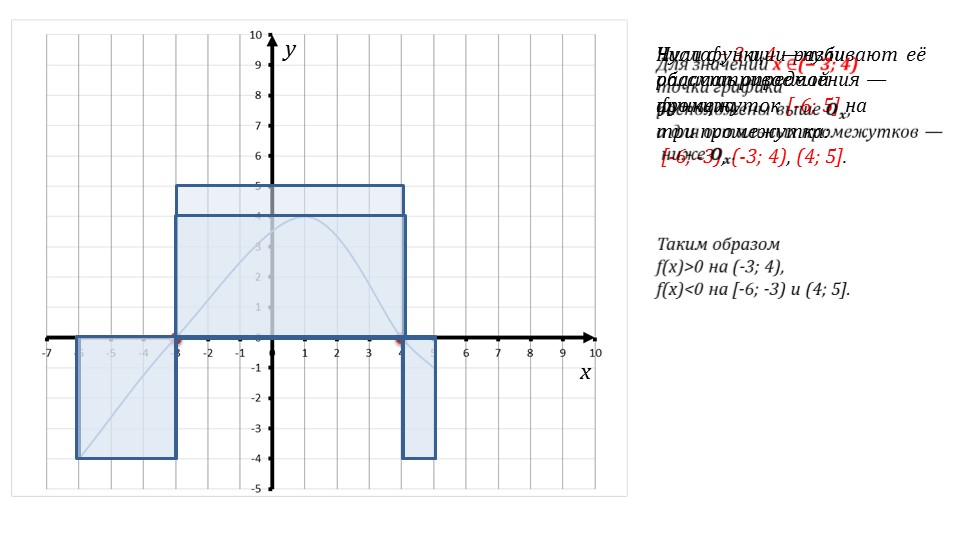
Далее представлен график функциональной зависимости f(x), в которой областью определения является множество значений на промежутке [-6;5]. На данном графике необходимо определить участки положительных и отрицательных значений функции. Для начала на графике отмечаются точки пересечения оси абсцисс. Это точки с координатами (-3;0), (4;0).

Данные точки разбивают график функции на участки, которые можно анализировать – это промежутки [-6;-3), (-3;4), (4;5]. На экране данные промежутки выделены для наглядной демонстрации свойств функции. Видно, что значения функции будут отрицательными на участках [-6;-3) и (4;5], а на участке (-3;4) – значения положительные. Таким образом, можно сделать вывод о важных свойствах данной функциональной зависимости: f(x)>0 на (3;4), f(x)<0 на [-6;-3) и (4;5]. Определение данного свойства выделено на слайде 5 как определение участков знакопостоянства.


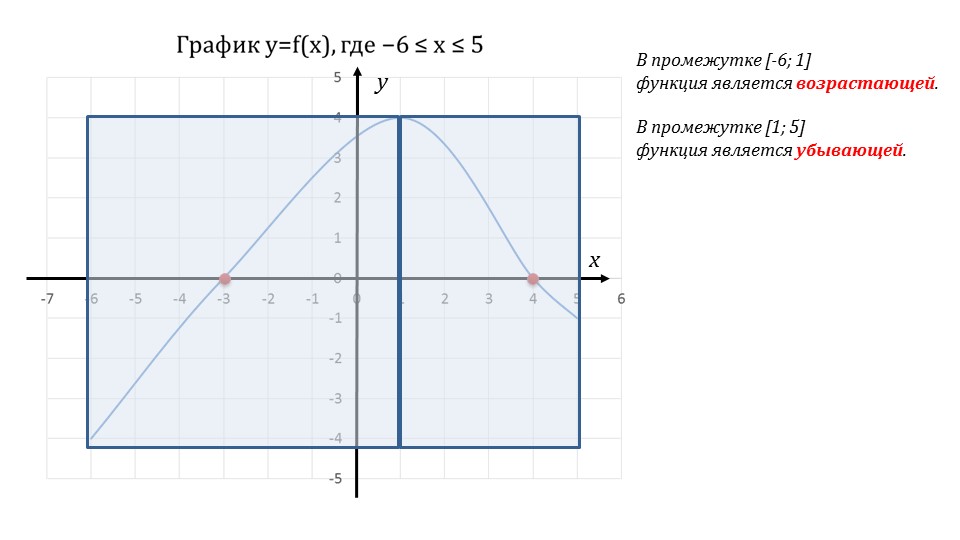
Рассмотрение свойства возрастания и убывания функции рассматривается также на приведенном выше примере графика функции. Для этого график функции разделен вертикальной осью, параллельной оси ординат с абсциссой 1. На рисунке видно, что при приближении слева к данной точке функция постоянно возрастает, а начиная с данной точки ее значение постоянно снижается. Соответствующий вывод, характеризующий данную функцию – промежуток [-6;1] – участок возрастания функции, а промежуток [1;5] – участок ее убывания. Пример сопровождает соответствующие определения возрастающей и убывающей на некотором промежутке функции.
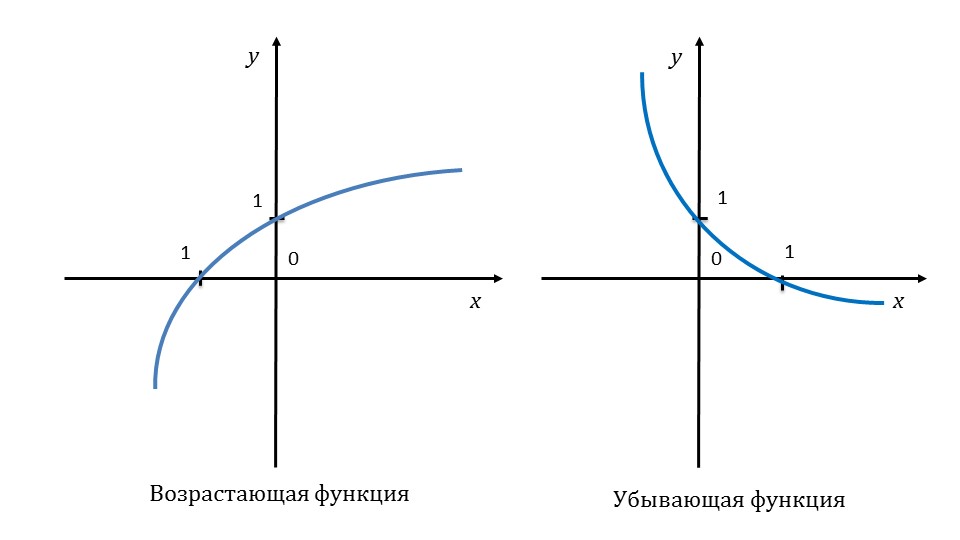
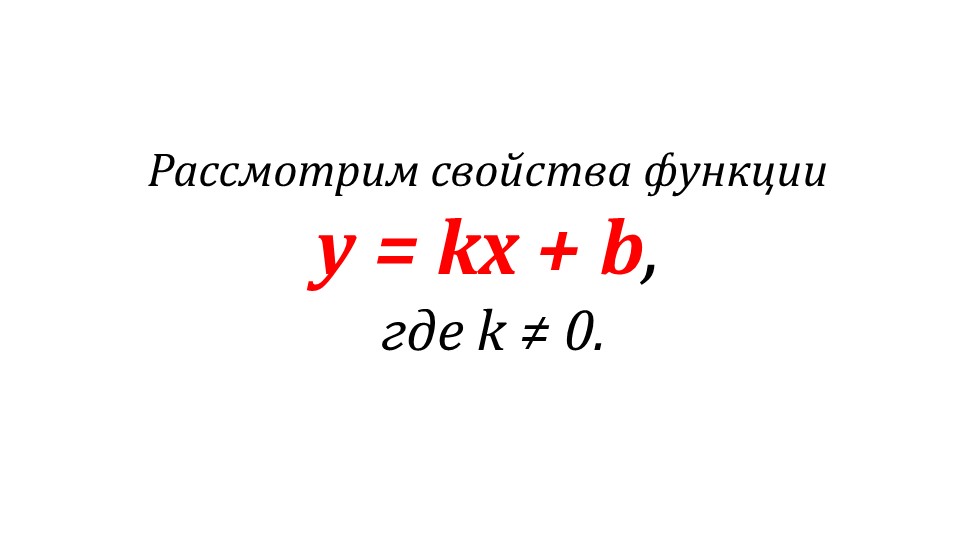
Возрастающая на промежутке функция определяется соответствием большего значения функции большему значению аргумента, а убывающая на промежутке функция определяется соответствием меньшего значения функции большему значению аргумента. На следующем слайде данное свойство определяется для возрастающей функции как возрастание по всей области определения, а также для убывающей функции как убывание по всей области определения. На слайде 9 приведены примеры графиков возрастающей и убывающей функций.


Далее демонстрируется пример рассмотрения свойств для линейной функции y=kx+b, где k≠0. Первым делом демонстрируется нахождение нулей функции. Утверждается, что нули функции находятся в точке с координатой x=-b/k. Данное утверждение доказывается решением уравнения kx+b=0, так как в данном случае y должен быть равен 0. В результате решения получаем подтверждение, что f(x)=0 при x=-b/k.
Далее для линейной функции рассматриваются участки знакопостоянства. Утверждается, что при k>0 значения функции отрицательные в промежутке (-;-b/k) и положительные в промежутке (-b/k;+). Для доказательства данных утверждений необходимо решить неравенства kx+b<0 и kx+b>0. В случае положительного коэффициента k решение принимает вид y<0 при x<-b/k, а y>0 при x>-b/k. Для положительного значения коэффициента k верно следующее: y<0 при x>-b/k, а y>0 при x<-b/k.


При анализе участков убывания и возрастания отмечается, что функция y=kx+b будет возрастающей при k>0 и убывающей при k<0. Для доказательства данного утверждения используется разность двух функциональных зависимостей, в первом из которых координаты некоторой точки графика функции (x1;y1), а во втором - (x2;y2). После произведенных вычислений значение разности значений функции равняется y2-y1=k(x2-x1). Видно, что при возрастании значения аргумента выражение в скобках принимает положительное значение. На следующем слайде отмечено, что знак произведения k(x2-x1) будет зависеть при возрастании аргумента только от знака коэффициента k. Расшифровка данного следствия описывается на слайде 15, где указано, что для положительного k будет k(x2-x1)>0, а следовательно, и y2>y1. При отрицательном значении k выражение k(x2-x1)<0, а следовательно, y2<y1. Вот и рассмотрены основные свойства функции y=kx+b.
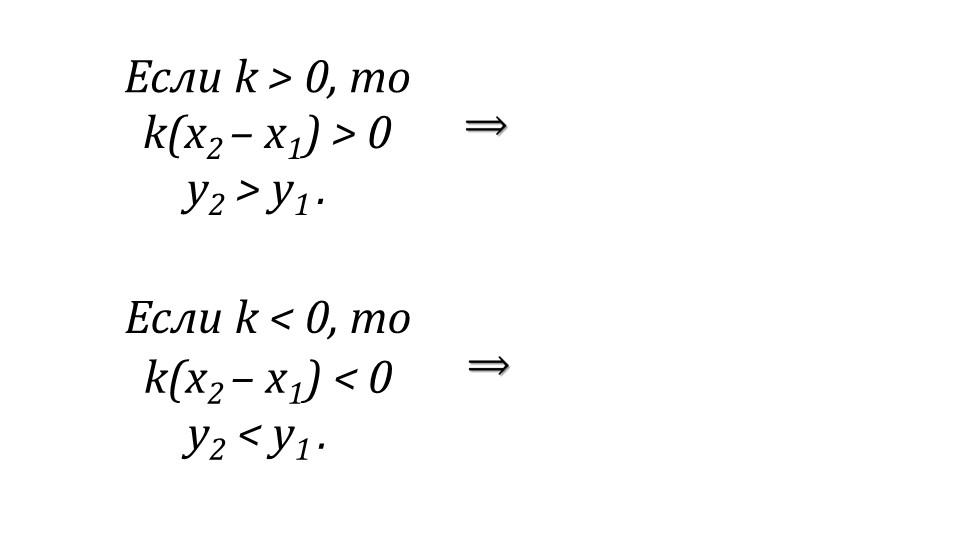
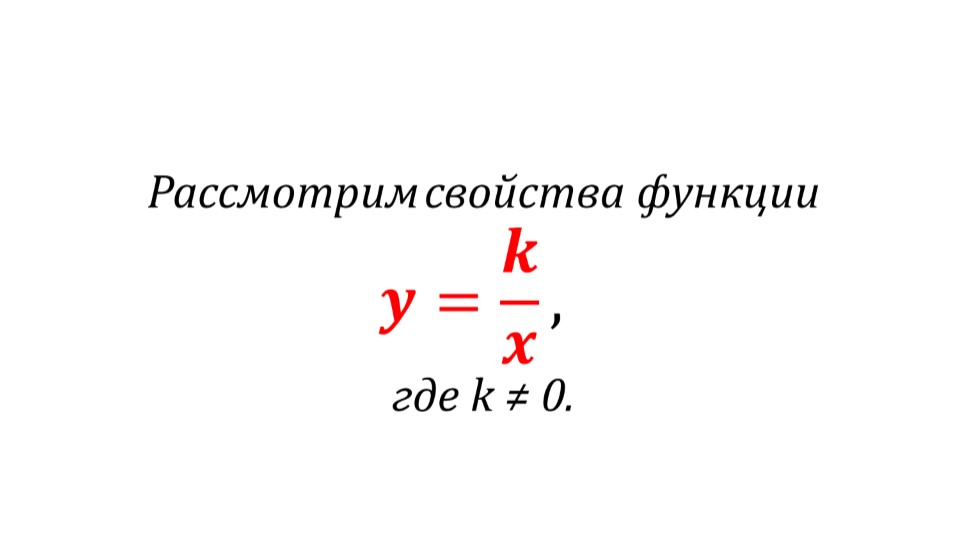
Далее рассматриваются свойства функции, представляющей собой обратную пропорциональную зависимость y=k/x, в которой k≠0. При рассмотрении нулей функции отмечается, что данная функция не имеет нулей. Так как числитель функции не принимает нулевое значение, а в знаменателе данной функции не может быть нуля, так как тогда выражение не имеет смысла, нулей у функции нет.
Следующее рассматриваемое свойство y=k/x, где k≠0 – участки знакопостоянства. Утверждается, что значения функции являются положительными на промежутке области определения (-;0) и отрицательными – на промежутке (0;+). Для доказательства данного утверждения решаются соответствующие неравенства. При их решении видно, что при положительных xи k значение функции будет положительным k/x>0, а при положительном k и отрицательном xзначения функции k/x<0. Таким образом, утверждение верно.


Последнее рассматриваемое свойство функции y=k/x – участки ее возрастания и убывания. Отмечается, что на обоих участках области определения (-;0) и (0;+) функция будет иметь одинаковые характеристики возрастания или убывания в зависимости от знака коэффициента k. При этом, если k>0, то y=k/x – убывающая на данных участках, а если k<0, то y=k/x – убывающая на обоих промежутках. Соответствующий вывод выделен на отдельном слайде, подчеркивая, что данная функция не является убывающей или возрастающей по всей области определения.


Презентация «Свойства функции» может быть использована для наглядного представления учебного материала на традиционном уроке в школе, а также послужить инструментом для дистанционного обучения. Также материал может быть рекомендован для самостоятельного изучения.
| Автор | |
|---|---|
| Дата добавления | 29.08.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 8133 |
| Номер материала | 624 |