
Презентация "Свойство биссектрисы угла и серединного перпендикуляра к отрезку"

Краткое описание документа:
Урок "Свойство биссектрисы угла и серединного перпендикуляра к отрезку" будет очень интересным и неутомительным, если при его проведении использовать обучающие мультимедийные файлы. Благодаря работе визуальной и слуховой памяти, а также, моторики, урок станет очень эффективным. Данная презентация сделает урок более красочным и понятным. Благодаря презентации, можно самостоятельно ознакомиться со свойствами биссектрисы и с серединным перпендикуляром.

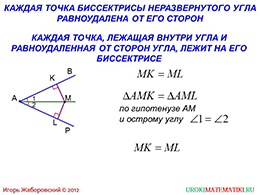
слайды 1-2 (Тема презентации "Свойство биссектрисы угла и серединного перпендикуляра к отрезку", теорема)
На первом слайде автором рассматривается неразвернутый угол PAB. Проведем биссектрису к ней. На иллюстрации она имеет зеленый цвет и обозначена как AM. Первое утверждение, которое дается выше, говорит о том, что любая точка, принадлежащая биссектрисе, будет иметь равное расстояние от первого и второго лучей, из которых состоит угол. Под расстоянием подразумевается высота, проведенная от данных точек до лучей. Этими высотами являются KM и LM. Можно увидеть, что острые углы также обозначены.
Обратное высказывание также будет верно. То есть, если некоторая точка является равноудаленной от сторон угла, то она лежит на биссектрисе. Учитель может предложить учащимся подумать и привести некоторый пример, который не удовлетворяет этим высказываниям. Разумеется, они не смогут привести ни одного примера, однако, это заставит их вникнуть глубже в суть высказываний.
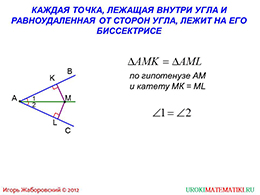
слайды 3-4 (теорема, следствие из теоремы)
Ниже приводится доказательство, в котором рассматриваются полученные треугольники. По признаку о равенстве треугольников, они являются равными, следовательно, и углы также равны. Таким образом, первая гипотеза доказана.
На следующем слайде доказывается верность второго высказывания. Доказательства не объемные и несложные. Их легко смогут повторить и школьники.
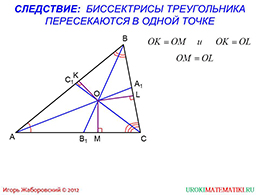
Рассмотрим следствие. Если рассмотреть произвольный треугольник, провести биссектрисы с каждой из вершин, то можно обратить внимание, что они пересекаются в одной точке. Доказывается следствие, опираясь на изученное высказывание. В качестве дополнительных построений, необходимо провести высоты, то есть рассмотреть расстояния от биссектрис до сторон углов при соответствующих вершинах.

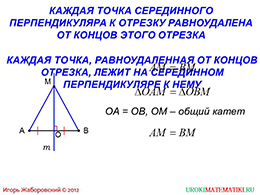
слайды 5-6 (определение серединного перпендикуляра к отрезку)
Перейдем к изучению серединного перпендикуляра. Исходя из названия, можно догадаться, что речь идет о перпендикуляре, а именно, о перпендикулярной прямой. Если разделить некоторый отрезок и провести через ее середину перпендикуляр, то он будет называться серединным. На рисунке видно, что прямая a является серединным перпендикуляром для отрезка AB.
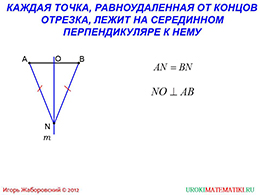
Следующий слайд проводит аналогичные рассуждения, которые уже встречались. Итак, если рассмотреть любую точку, лежащую на серединном перпендикуляре некоторого отрезка, то расстояния от этой точки до концов отрезка будут равны. Обратное высказывание является также верным. Доказательство приводится очень наглядно. Рассматриваются полученные в результате дополнительных построениях треугольника, которые являются прямоугольными. Школьник, просматривающий презентацию, может попробовать самостоятельно проделать доказательство.
слайды 7-8 (теорема, следствие)
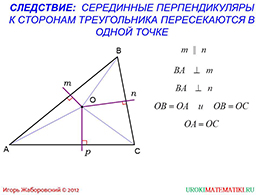
Завершающий слайд содержит следствие от предыдущего высказывания. Оно подобно следствию касательно биссектрис, которое рассматривалось в данной презентации немного раньше. Итак, если провести три серединных перпендикуляров в произвольном треугольнике, то есть к каждой из сторон, то они будут пересекаться в одной точке. Приводится доказательство.
Как видно, в данном методическом электронном пособии содержатся множество доказательств. По правде говоря, они не являются сложными, однако, не стоит жалеть свое время для того, чтобы понять их идеально. Если доказательство хорошо понять, то и не придется зазубривать теоремы.
На данном уроке школьники ознакомились с понятием серединный перпендикуляр и изучили свойства биссектрисы и серединного перпендикуляра.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 11054 |
| Номер материала | 352 |