
Урок "Теорема о вписанном угле"

Краткое описание документа:
Прежде чем мы приступим к подробному изучению теоремы о вписанном угле, а также сопутствующих свойств, напомним основные определения в данной области геометрии.
Окружностью называют геометрическую фигуру, все точки которой равноудалены от некоего общего центра, который именуют центром окружности и, чаще всего, обозначают буквой О. Окружность обычно рассматривается в двух состояниях – вписанной и описанной с разными многоугольниками. Такой симбиоз порождает множество частных выводов и теорем, помогающих досконально разобрать свойства многих фигур.
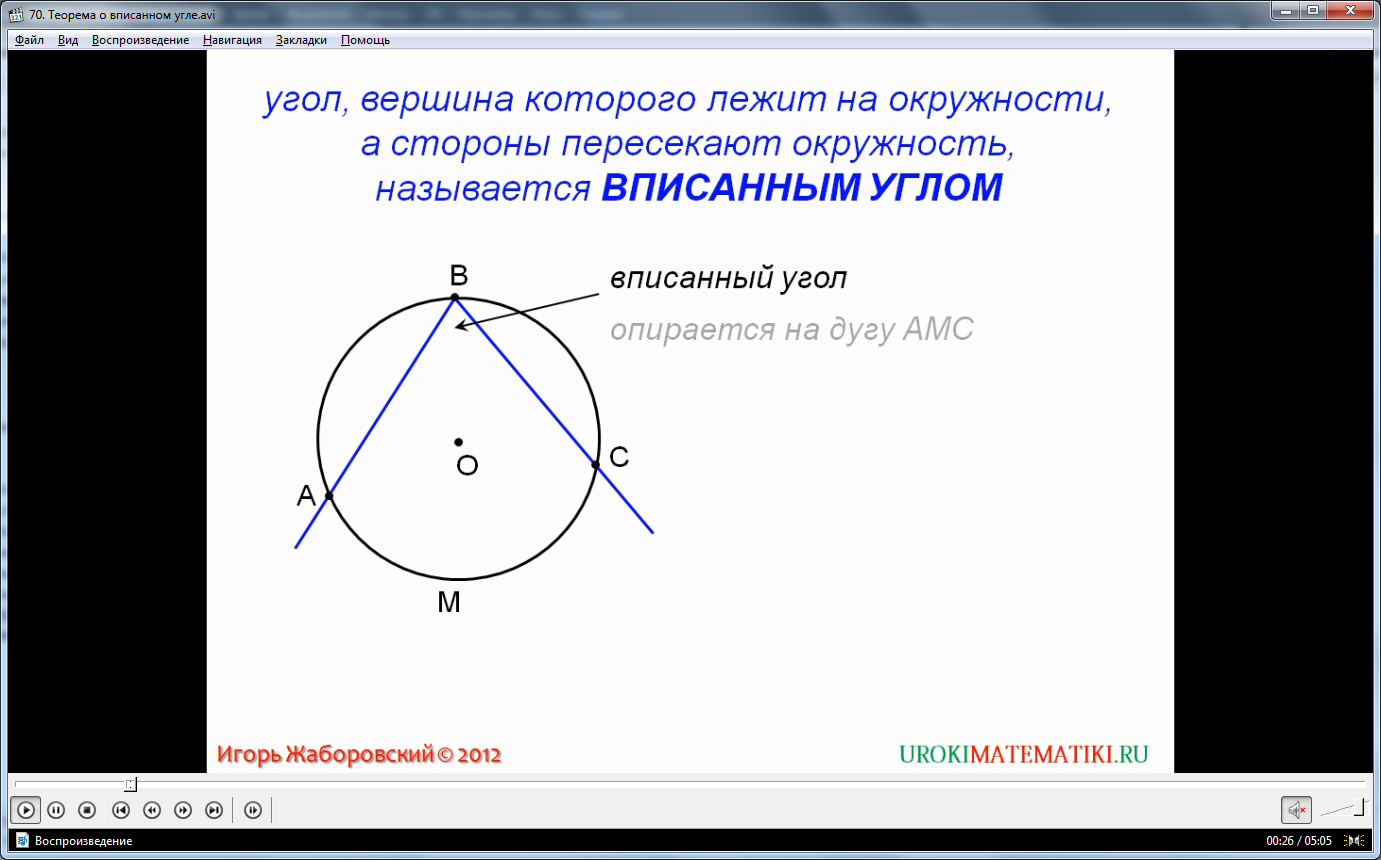
В представляемом видео уроке мы рассмотрим вписанный угол. Вписанный в окружность угол – это угол, вершина которого лежит на окружности, а стороны где-либо её пересекают.
Для подробного ознакомления с темой видео необходимо также усвоить понятия биссектрисы, дуги и хорды. Биссектриса – это линия (луч по геометрии), выходящая из вершины угла, и делящая угол на два равных угла. Это понятие относится к самому углу, в то время, как хорда и дуга – термины деталей окружности. Хорда – это отрезок, соединяющий две произвольные точки на окружности. Дуга – это участок окружности между двумя произвольными точками, лежащими на ней.
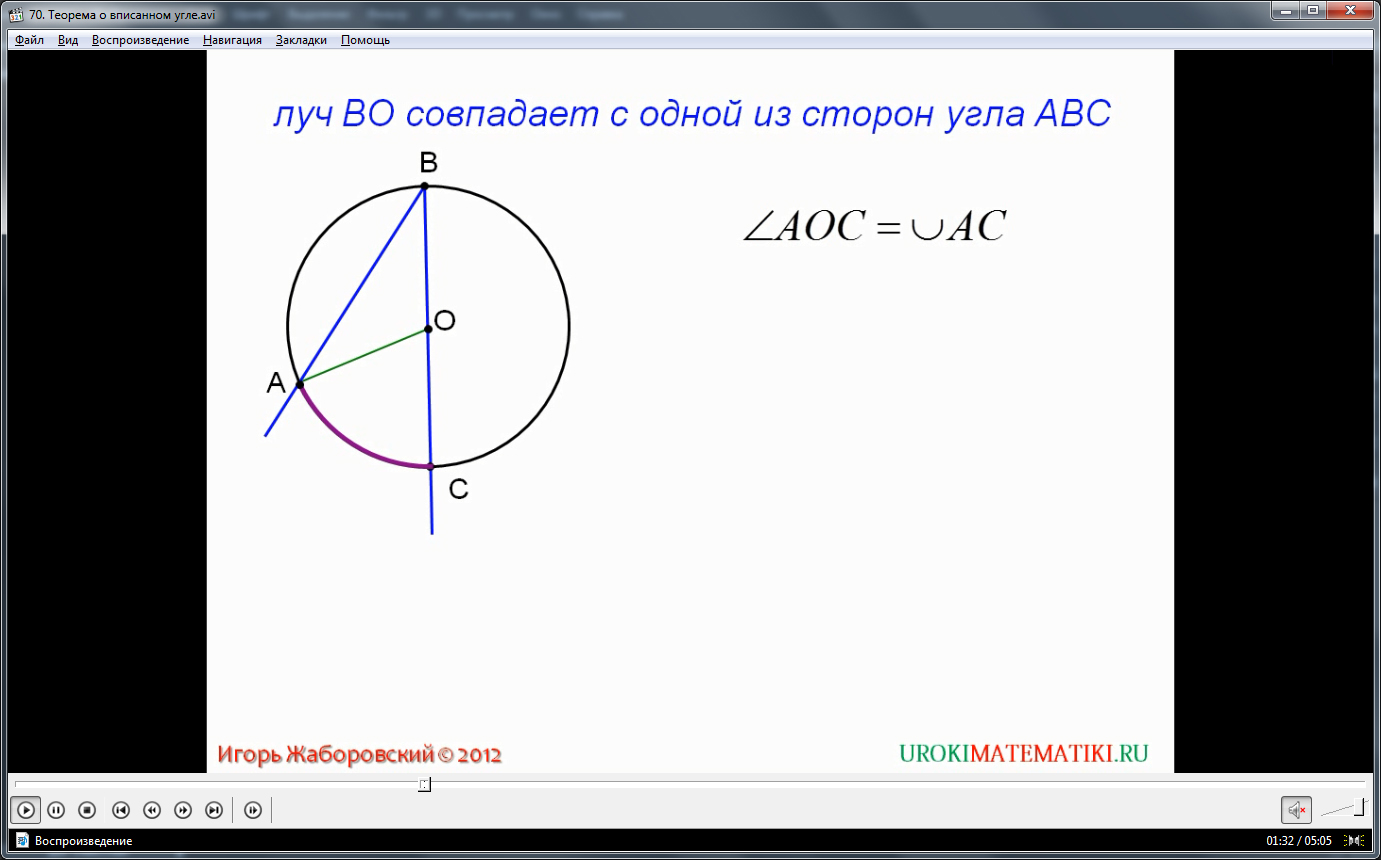
Необходимо резюмировать, что любой вписанный угол опирается на определенную дугу окружности, равную двойному значению самого угла. Например, рассмотрим окружность с центром О, которая описана вокруг угла АВС так, что вершина угла В лежит на окружности, а стороны АВ и ВС пересекают её в точках А и С. Как мы видим, угол АВС является вписанным в окружность О, опираясь на дугу АС. При этом, угол АВС = 1/2 дуги АС.

Проведем в нашей окружности луч ВО, который будет являться радиусом окружности. Он соединяет вершину угла и центр окружности. В зависимости от своего расположения относительно сторон угла, этот луч порождает некоторые свойства:
Если луч ВО делит угол ровно пополам, т.е. центр окружности располагается внутри этого угла, то, при этом, луч ВО является биссектрисой угла АВС, угол АВО = углу ОВС. Равенство последних углов обуславливает равенство дуг АО1 и О1С. Где О1 – это некая точка, лежащая на дуге АС и в которой луч ВО пересекает окружность. Кроме того, точка О1 является срединной точкой для дуги АС.
Если луч ВО совпадает с любой стороной угла, к примеру, с отрезком ВС, то вытекает следующее соотношение: центральный угол дуги АО1, т.е. угол АОО1 численно равен двум углам АВС. Для того, чтобы это доказать, проведем отрезок АО, соединяющий центр окружности с точкой пересечения её и стороны угла. При наших условиях, ВС идентично ВО1, АВО1 является вписанным углом. Так как отрезки АО и ВО являются радиусами, они равны между собой, а треугольник АВО является равнобедренным. По свойству всех равнобедренных треугольников, углы при основании его равны, т.е. угол АВО1 равен углу ВАО. Так как сумма всех углов в треугольнике равна 180 градусам, справедливо будет записать:
АВО + ВАО + ВОА = 180
2АВО + ВОА = 180
ВОА = 180 – 2АВО
С другой стороны, угол ВОА является смежным углом для АОО1 (ВО1 – диаметр по определению), и по свойству смежных углов получаем:
ВОА = 180 – АОО1
180 – 2АВО = 180 – АОО1
2АВО = АОО1
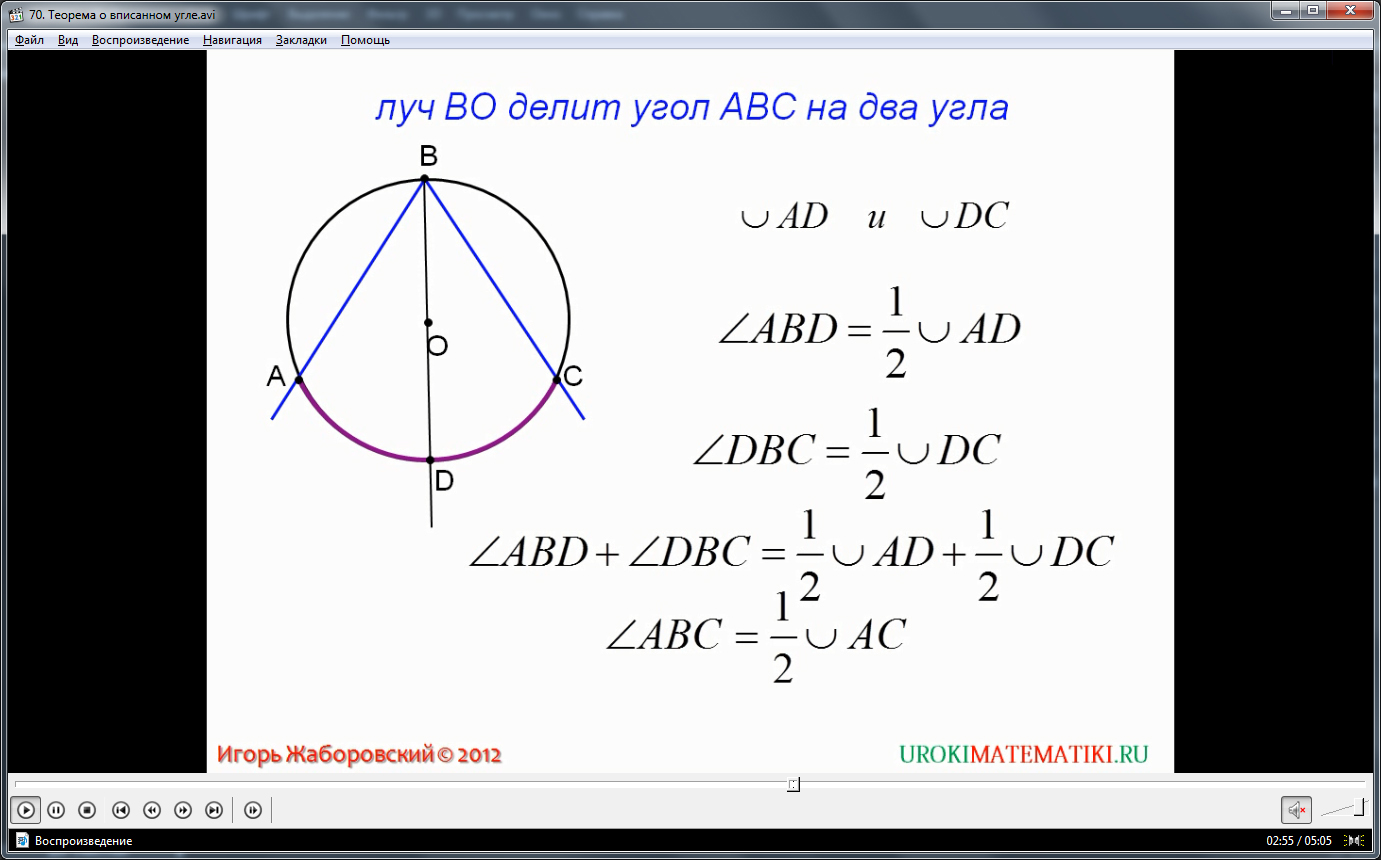
Что и требовалось доказать. Если луч ВО не совпадает со сторонами угла и лежит вне его, то, в данном случае, нельзя вывести полезных свойств.
Из всего вышесказанного вытекает несколько примечательных выводов. На видео представлены наглядные иллюстрации данных выводов.
Если вписанные углы опираются на одну дугу, то они равны между собой. При этом, дуга необязательно должна быть единой в эвклидовом пространстве для обеих углов – имеется в виду её угловое значение при неизменном радиусе окружности.
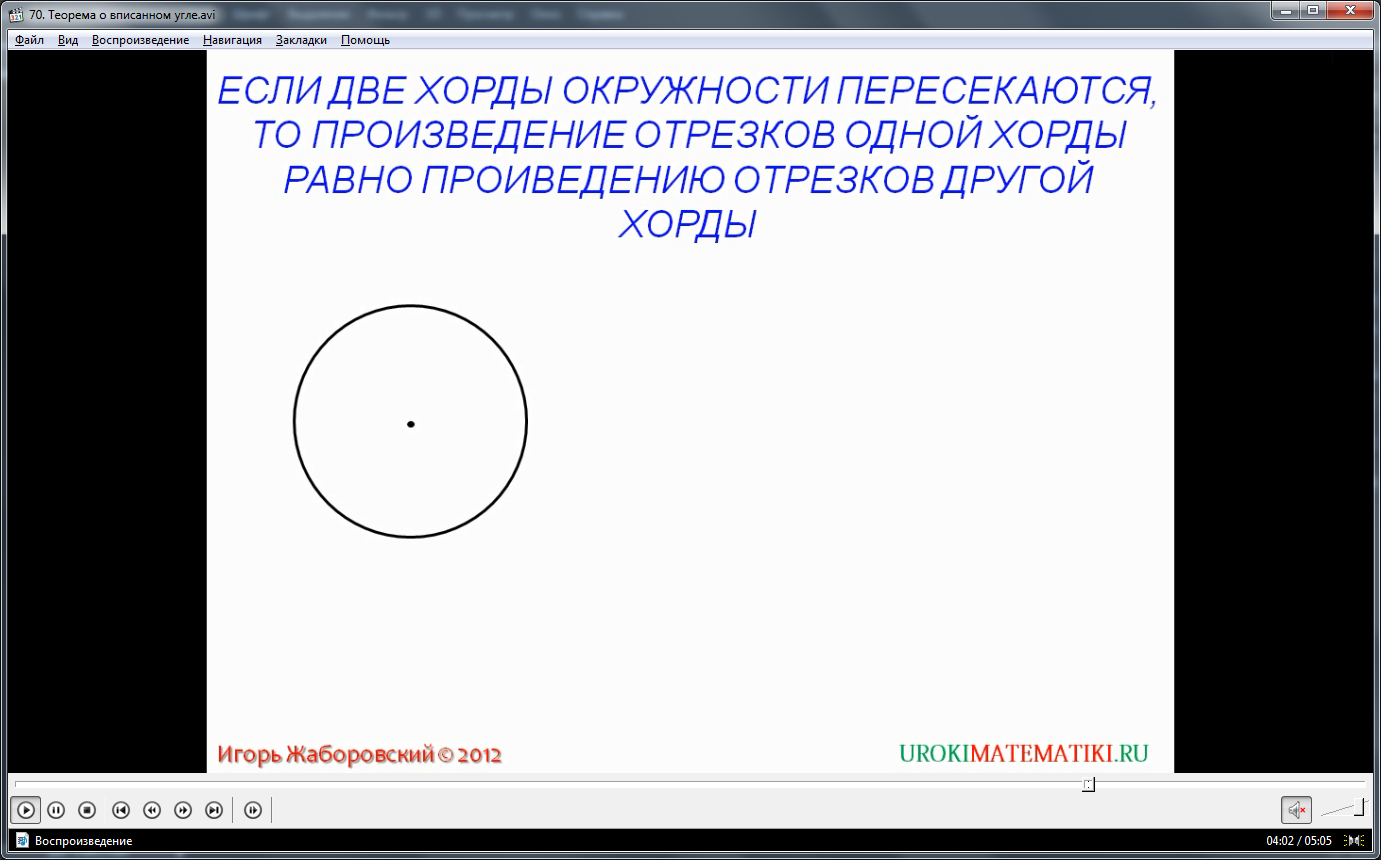
Если вписанный угол опирается на полуокружность (развернутую дугу, центральный угол которой равен 180 градусам), то он равен 90 градусам. Стоит отметить, что в одной и той же окружности, на одной заданной дуге, можно построить множество вписанных углов, даже при жестко определенном размере дуги. Если две хорды, принадлежащие одной окружности, пересекаются между собой, то образуемые ими отрезки, при произведении друг на друга, будут равны.
| Автор | |
|---|---|
| Дата добавления | 01.08.2014 |
| Раздел | Геометрия |
| Подраздел | Видеоурок |
| Просмотров | 7418 |
| Номер материала | 608 |