
Презентация "Теорема о прямой, перпендикулярной к плоскости"

Краткое описание документа:
Презентация «Теорема о прямой, перпендикулярной к плоскости» - наглядное пособие для демонстрации учебного материала по данной теме на уроке геометрии. Она предназначена для формирования умения доказывать геометрические утверждения и решать геометрические задачи с использование теоретических знаний о перпендикулярности прямой и плоскости, повышения эффективности урока математики. В ходе презентации рассматриваются соответствующие теоремы с доказательством справедливости утверждения, а также приводятся примеры решения задач с использованием данных теоретических знаний.


Презентация – одна из наиболее эффективный форм наглядного представления учебного материала. Особенно ее приемы полезны при демонстрации свойств объемных тел и объектов. В презентации используется выделение цветом, анимационные эффекты, возможность включать схемы и рисунки, поэтому в ней легко воспроизвести построения, сделать их более доступными для понимания учеников. Использование приемов для создания ярких, привлекательных слайдов способствует удержанию внимания учеников на изучаемом предмете, а также быстрому формированию у них необходимых представлений о понятиях.

Презентация начинается с напоминания признака перпендикулярности прямой и плоскости, изученных на предыдущих уроках. На слайде в рамку выделен признак, утверждающий о перпендикулярности прямой к плоскости, если она перпендикулярна двум пересекающимся прямым на ней. Также напоминается теорема о перпендикулярности прямой к плоскости, если параллельная ей прямая перпендикулярна к этой плоскости. На третьем слайде представлена теорема, обратная к последней – о параллельности двух прямых, перпендикулярных к плоскости.
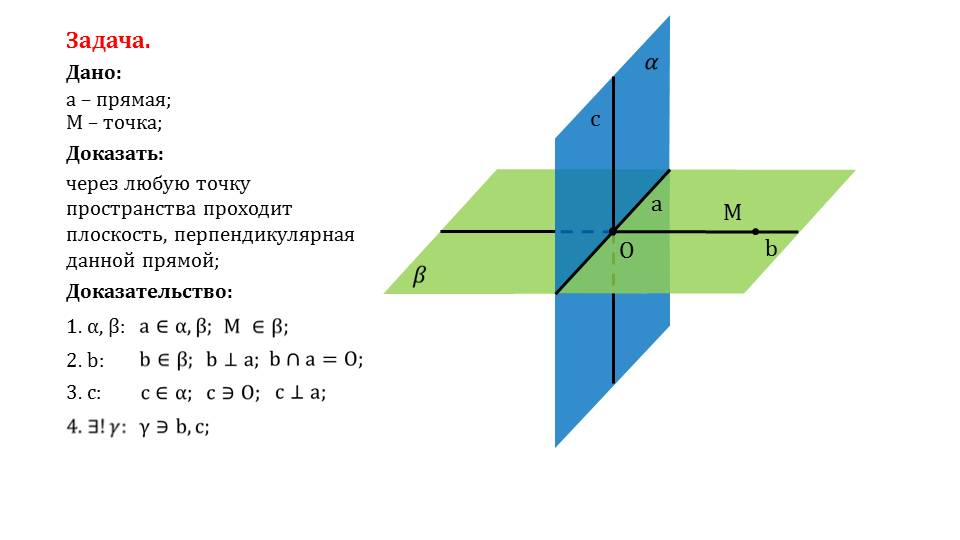
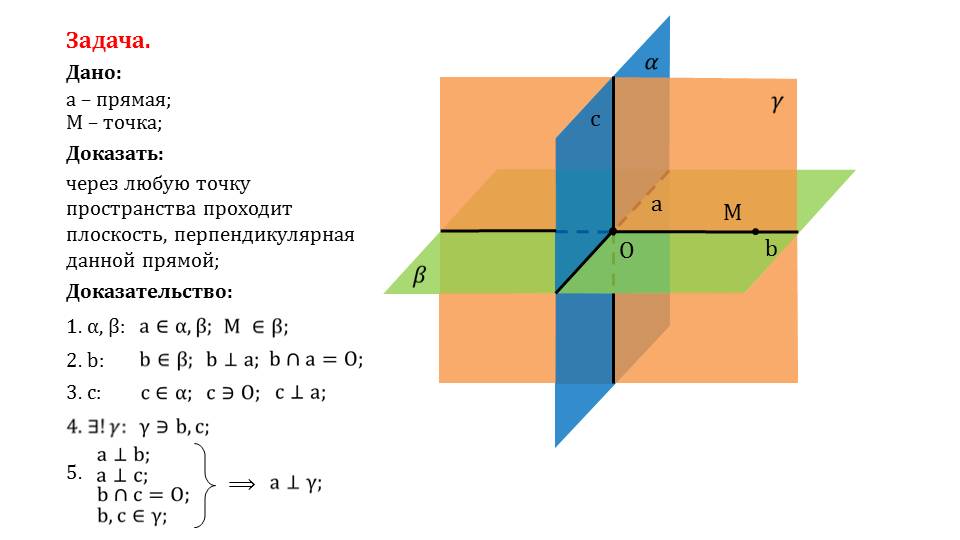
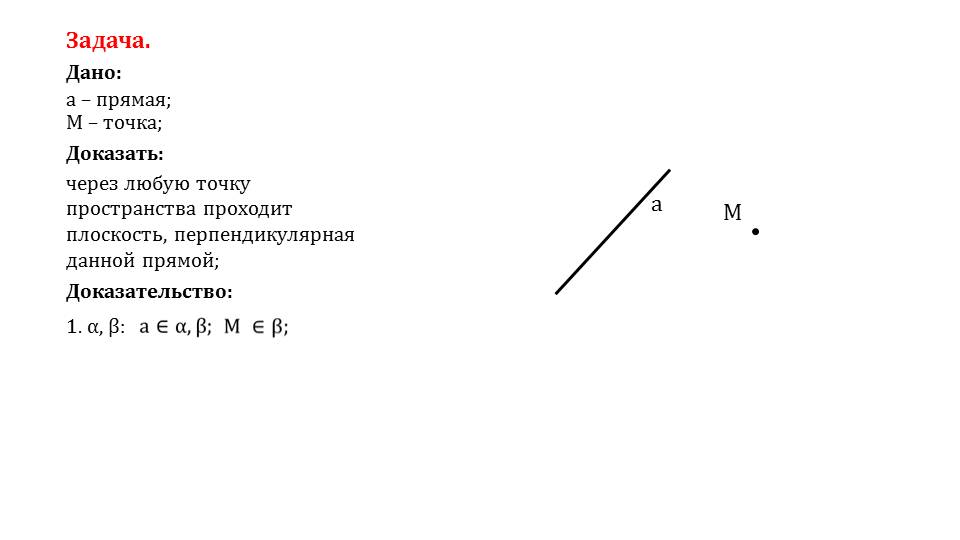
Далее рассматривается решение задачи, в которой даны произвольная точка М и прямая а. Необходимо доказать, что через любую точку в пространстве можно провести плоскость, перпендикулярную этой прямой. Вначале строятся некоторые плоскости α и β, при чем М принадлежит плоскости β, а прямая а относится к обеим плоскостям. На рисунке α изображается синим цветом, а β – зеленым. Через точку М на плоскости β проводится прямая b, перпендикулярная к прямой а. Точка их пересечения называется точкой О. Затем в плоскости α проводится прямая с, перпендикулярная к прямой а и проходящая через точку О. Отмечается, что существует некоторая плоскость γ, которой будут принадлежать прямые b и с. Из построения следует перпендикулярность прямой а к прямым b и с, пересекающимся в точке О, а b и с принадлежат плоскости γ. Выполнение этих условий ведет к выводу о перпендикулярности прямой а и плоскости γ. Утверждение доказано.

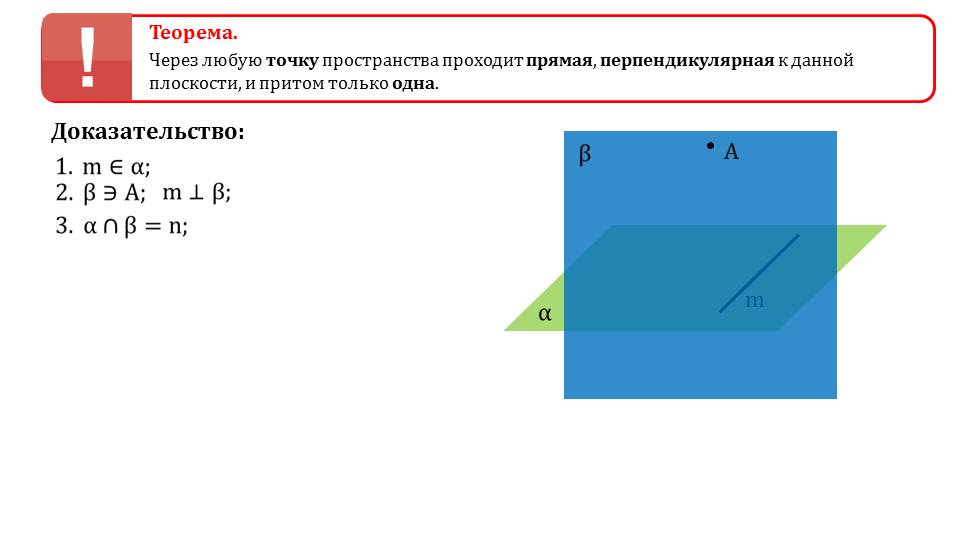
На следующем слайде формулируется теорема существовании единственной прямой проходящей через указанную точку в пространстве и перпендикулярной к данной плоскости. Далее рассматривается ее доказательство. На рисунке изображаются плоскости α и β. На плоскости α строится прямая m, а на плоскости β отмечается точка А. указано, что прямая m перпендикулярна плоскости β. Плоскости пересекаются по прямой n. В плоскости β через точку А строится вспомогательная прямая р, перпендикулярная прямой n. Так как m перпендикулярна плоскости β, то перпендикулярна всем прямым в ней, в том числе р, принадлежащей β. Перпендикулярность р к прямым m и n, принадлежащих α и пересекающихся между собой означает перпендикулярность прямой р плоскости α. Ри этом р – искомая точка.
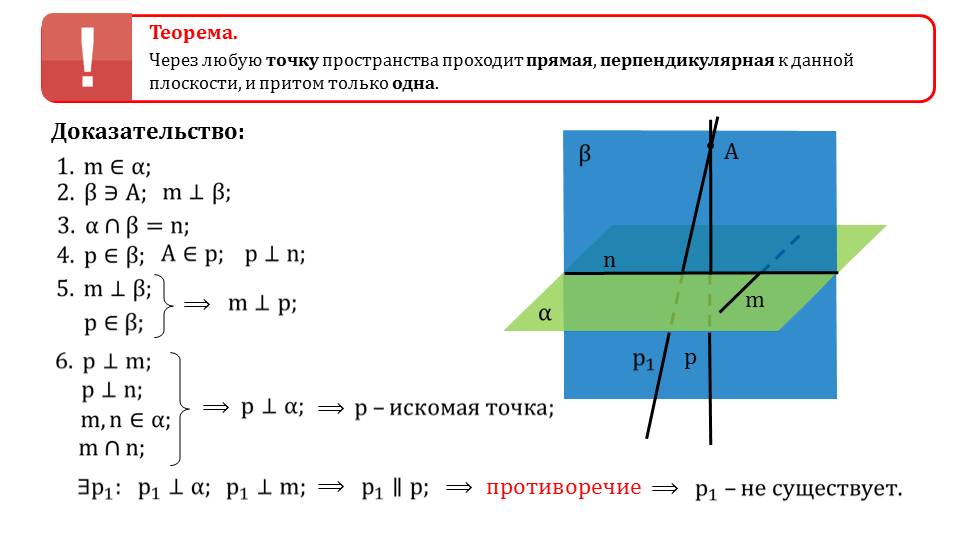
Единственность прямой, перпендикулярной к плоскости и проходящей через указанную точку доказывается методом от противного. Предполагается существование еще одной такой прямой р1, но из ее перпендикулярности плоскости α и прямой m следует параллельность р1 и р. Придя к противоречию, мы доказали утверждение.
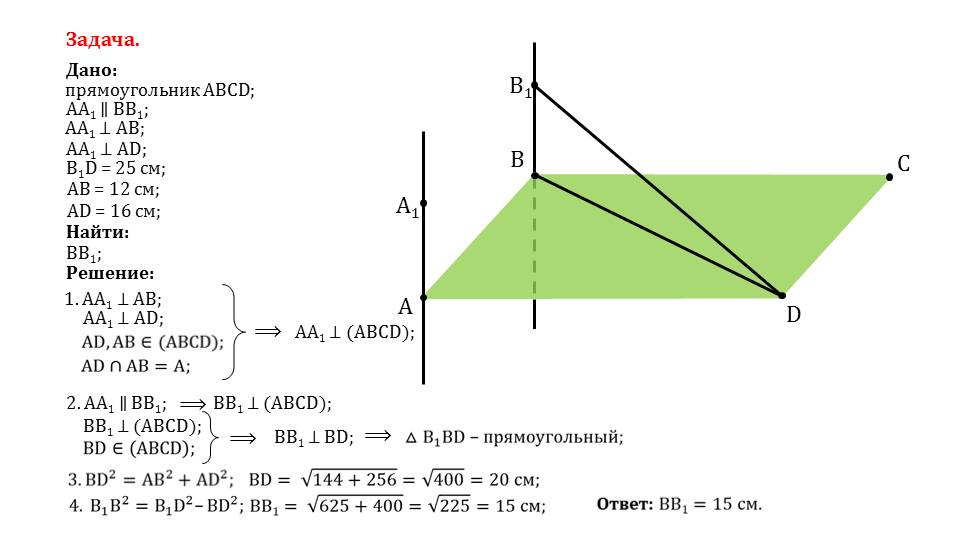
Далее рассматривается решение двух геометрических задач. В первой задаче дан прямоугольник ABCD, через вершины которого А и В проходят перпендикулярные к плоскости ABCD прямые АА1 и ВВ1. Они параллельны между собой и перпендикулярны к сторонам прямоугольника. При этом B1D=25 см, АВ=12 см, АD=16 см. Необходимо найти длину отрезка ВВ1. Так как АА1 перпендикулярна сторонам прямоугольника, то перпендикулярна и плоскости, в которой он лежит. Из параллельности построенных прямых вытекает и перпендикулярность ВВ1 к плоскости (ABCD), а следовательно, и к диагонали прямоугольника BD. Созданный таким образом треугольник ΔВ1ВD является прямоугольным. Используя теорему Пифагора, отмечаем, что BD=√(144+256)=20 см. Таким же образом определяем ВВ1=√(625+400)=√225=15. Ответ найден.
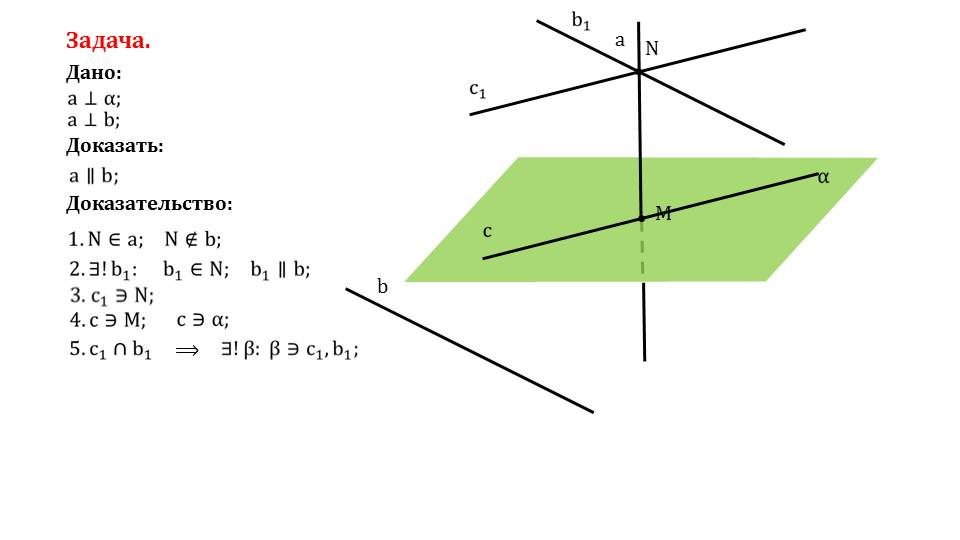
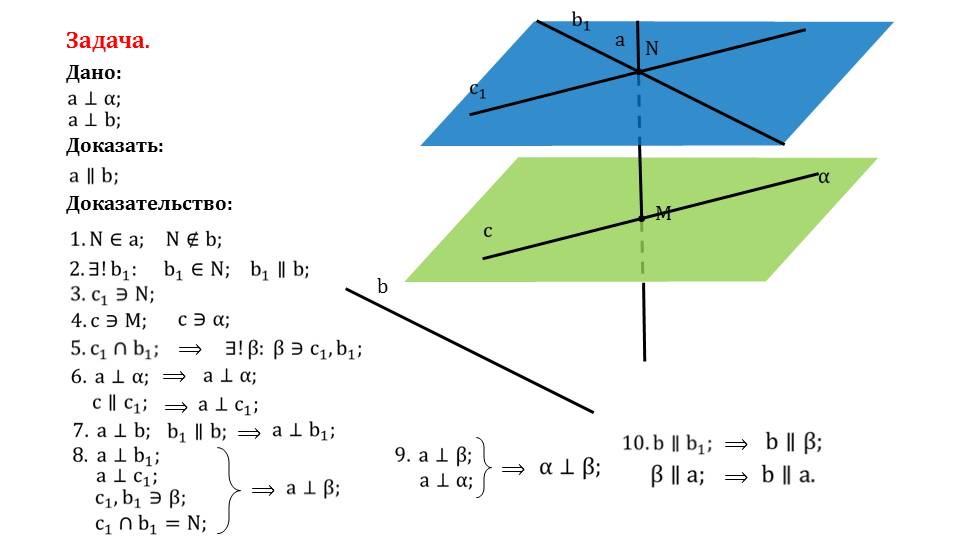
В последней задаче дана прямая, перпендикулярная плоскости α и перпендикулярная к некоторой прямой bв пространстве. Необходимо доказать параллельность прямой b плоскости α. На прямой а отмечается точка N, которая принадлежит а, но не принадлежит b.Проведем через эту точку прямую b1, параллельную b. Через точку М на плоскости α проведена прямая с. Через N проводится прямая с1, параллельная с. Пересекающиеся прямые с1 и b1 принадлежат некоторой плоскости β. Так как с параллельна с1, а а перпендикулярна α, то а перпендикулярна и с1.из перпендикулярности прямых aи b следует перпендикулярность а к b1 и к с1. Так как они принадлежат плоскости β и пересекаются в точке N, то прямая а перпендикулярна плоскости β. Аналогично доказываем параллельность плоскостей α и β, и, соответственно, прямой b и плоскости α. Задача решена.
Презентация «Теорема о прямой, перпендикулярной к плоскости» может сопровождать объяснение учителя на уроке, а также служить наглядным пособием для проведения дистанционного обучения. Материал может быть рекомендован ученику, самостоятельно осваивающему предмет или требующему дополнительного объяснения темы.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 11153 |
| Номер материала | 890 |