
Презентация "Трёхгранный угол"

Краткое описание документа:
Презентация «Трёхгранный угол» - наглядное пособие для повышения эффективности урока геометрии по данной теме. Пособие содержит наглядный материал для формирования у учеников понятия трехгранного угла, умения доказывать теорему о трехгранном угле, решать задачи с использованием теоретических сведений о свойствах трехгранного угла. В ходе презентации демонстрируется материал, напоминающий ученикам полученные ранее теоретические сведения, необходимые для освоения новой темы, вводится понятие трехгранного угла, доказывается важная теорема по теме, демонстрируется описание решения задачи.
Презентация – средство наглядности, использование которого имеет много преимуществ по сравнению с другими средствами. В презентации могут использоваться приемы, которые помогают представить информацию в виде, удобном для понимания темы учениками, быстрого запоминания. Благодаря таким приемам, внимание учеников удерживается на изучаемом предмете. Анимационные эффекты дают возможность структурировать подаваемую информацию, сделать построения приближенными к традиционной демонстрации свойств и элементов геометрических фигур на классной доске.
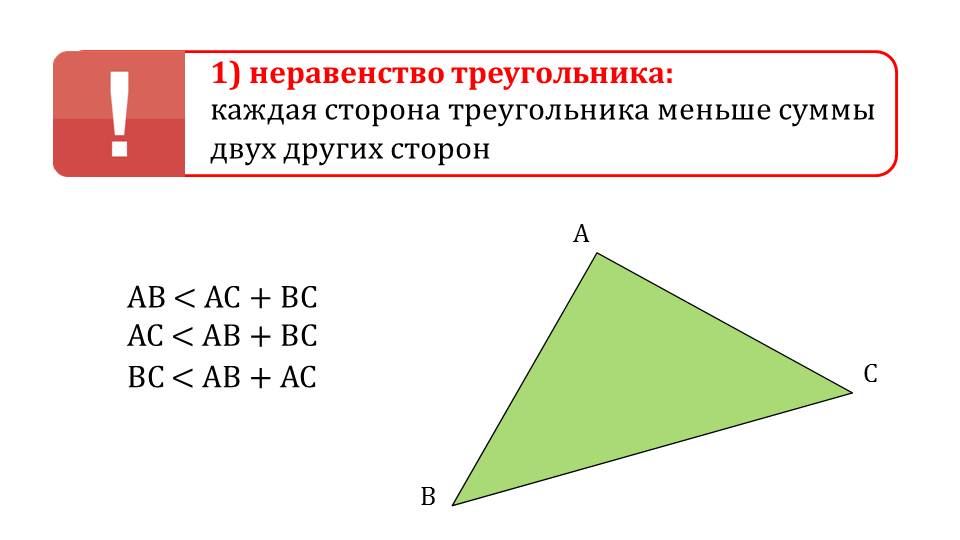

Демонстрация начинается с напоминания ученикам изученного ранее материала, который используется при изучении новой темы. Напоминаются сведения о свойствах треугольника. На первом слайде представлено неравенство треугольника, утверждающее, что длина каждой стороны треугольника меньше суммы двух оставшихся сторон. Под свойством расположен рисунок, где изображен треугольник ΔАВС, рядом с которым написаны верные неравенства АВ<AC+BC, AC<AB+BC, BC<AB+AC.
Второй слайд напоминает ученикам суть теоремы о соотношении сторон и углов треугольника, в которой утверждается, что напротив большей стороны треугольника лежит больший угол. Под текстом теоремы изображен треугольник RQL, на примере которого представлены верные неравенства из данной теоремы: для RQ>RL>QL, верно ∠L>∠Q>∠R.
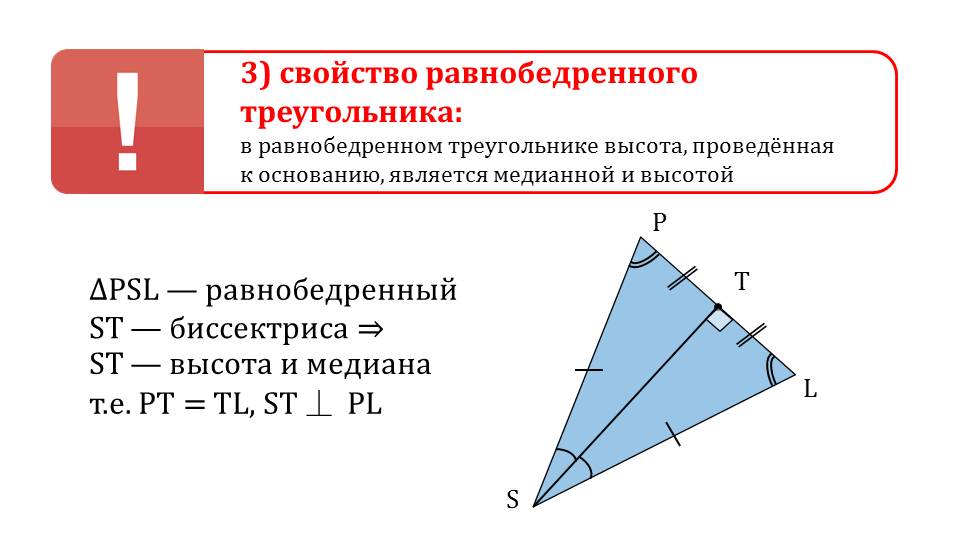
На третьем слайде представлено свойство равнобедренного треугольника о том, что высота, проведенная к основанию, является биссектрисой и медианой. Текст теоремы сопровождается рисунком, на котором изображен треугольник ΔPSL. На рисунке отмечены равные стороны и углы треугольника. Рядом указано, что представлен равнобедренный треугольник ΔPSL, биссектриса ST, которая является медианой и высотой, то есть PT=TL, а ST перпендикулярна PL.
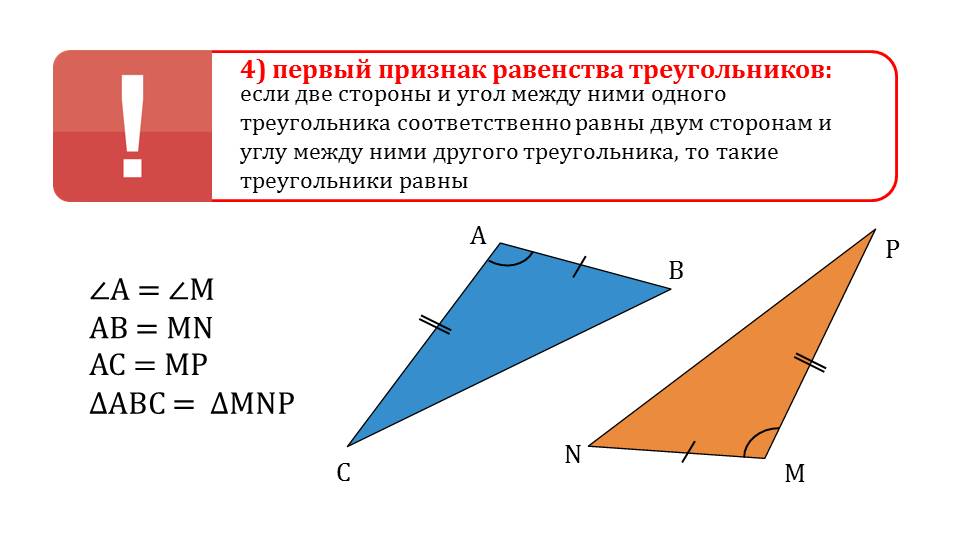
Четвертый слайд демонстрирует первый признак равенства треугольников, в котором указано, что треугольники равны, если в них равны две соответствующие стороны и углы между ними. Под текстом теоремы изображены рисунки двух треугольников ΔАВС и ΔNNPM. На рисунке отмечены равные стороны и углы треугольников, рядом располагается соответствующая запись ∠А=∠М, АВ=MN, АС=МР и равенство треугольников ΔАВС=ΔMNP.
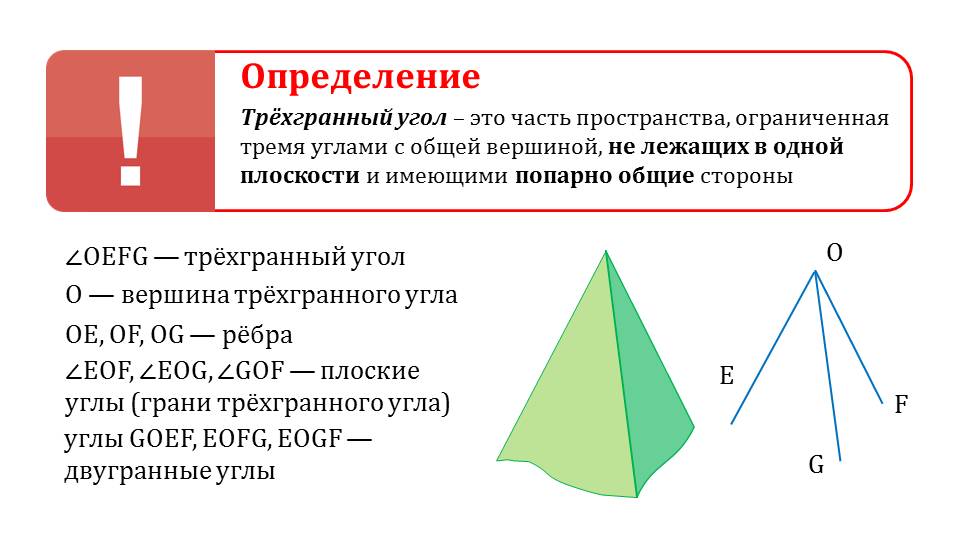
Далее представлено определение трехгранного угла как части пространства, что ограничена тремя углами, у которых общая вершина, стороны, не лежащие в одной плоскости. Определение выделено цветом для лучшего запоминания. Под текстом определения помещено изображение трехгранного угла, который также обозначается ∠OEFG с вершиной в точке О, ребрами OE, OF, OG. При этом также отмечены плоские углы, являющиеся ребрами трехгранного угла - ∠EOF, ∠EOG, ∠GOF, а также двугранные углы GOEF, EOFG, EOGF.
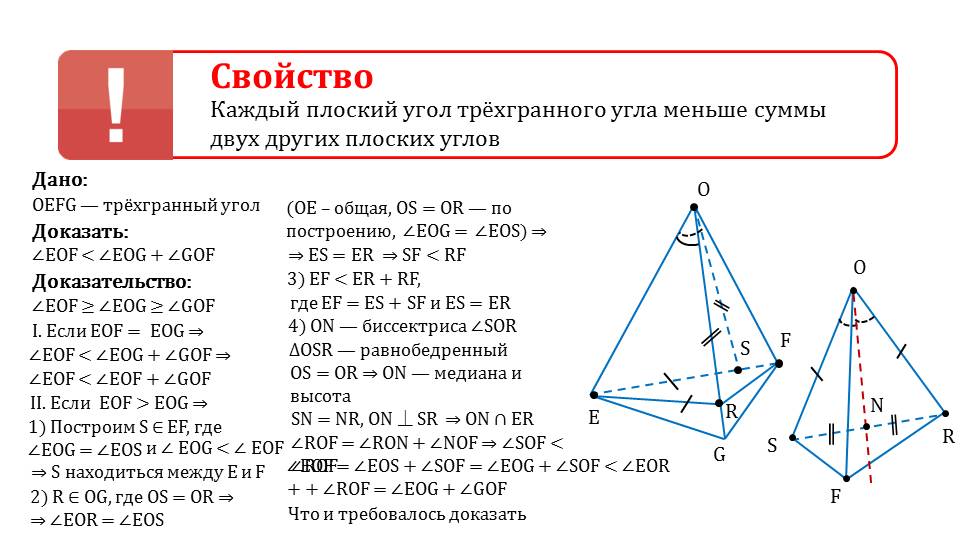
На слайде 6 представлено свойство трехгранного угла, утверждающего, что каждый плоский угол меньше суммы двух оставшихся углов. Доказательство сопровождается рисунком, на котором изображен трехгранный угол OEFG. Необходимо доказать справедливость неравенства ∠EOF<∠EOG+∠GOF. Доказательство состоит из нескольких частей, рассматривая различные случаи соотношения плоских углов: если два угла равны EOF= EOG, а также если EOF>EOG. Используя свойства треугольников, о которых упоминалось в начале презентации, доказывается утверждение.
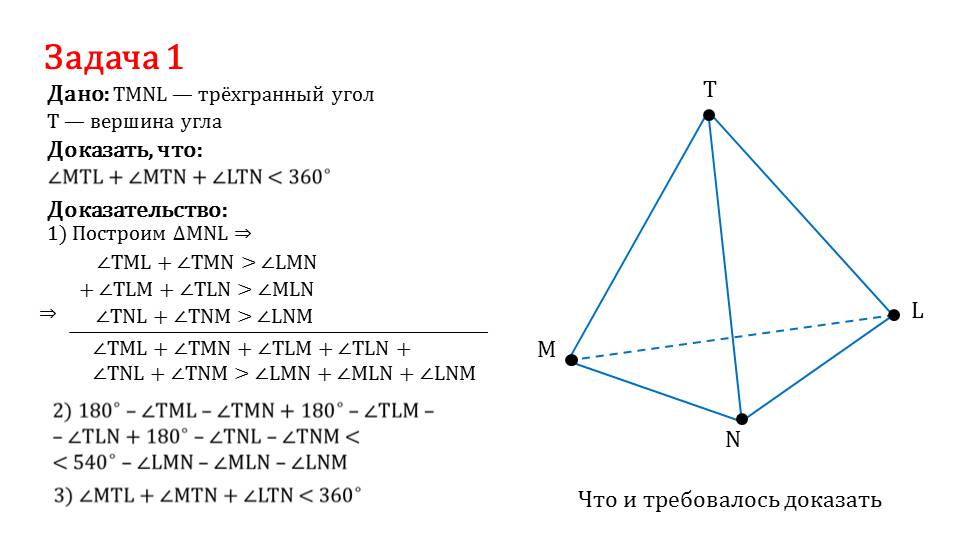
На последнем слайде презентации представлено описание решения задачи, в которой представлен трехгранный угол TMNL с вершиной в точке Т. Необходимо доказать неравенство ∠ MTL+∠ MTN+∠ LTN<360°. Чтобы доказать неравенство, строится треугольник ΔMNL, в котором выполняются неравенства, верные для треугольников. Используя приведенные в начале демонстрации знания, полученные ранее, доказывается справедливость неравенства. Складывая неравенства ∠ TML+∠ TMN>∠LMN, ∠ TLM+∠ TLN>∠MLN и ∠ TNL+∠ TNM>∠LNM получаем неравенство ∠ TML+∠ TMN + ∠ TLM+∠ TLN + ∠ TNL+∠ TNM>∠LNM+∠LMN+∠MLN. Зная теорему о сумме углов треугольника заменяем сумму углов значением 180°, из чего затем получаем искомое неравенство.
Презентация «Трёхгранный угол» помогает легче достичь целей обучения на традиционном уроке геометрии в школе. Также данное пособие пригодится учителю, который обучает своих учеников дистанционно. При необходимости ученикам освоить тему самостоятельно, им может быть рекомендован материал как пособие, детально раскрывающее предмет изучения.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 9110 |
| Номер материала | 897 |