
Презентация "Угол между прямой и плоскостью"

Краткое описание документа:
Презентация «Угол между прямой и плоскостью» представляет наглядный материал, раскрывающий данную тему. В ходе презентации вводится понятие проекции наклонной, а также угла, образованного прямой и плоскостью, демонстрируются важные теоретические выводы, знание которых поможет в решении стереометрических задач, описывается решение задач, где применяются данные знания. С помощью презентации учителю легче достигать учебных целей, формировать умение решать геометрические задачи.
В презентации используется анимация, помогающая сделать построения более приближенными к традиционной наглядности – на классной доске. При этом четкое и разноцветное изображение на экране должно быть хорошо видно с любой точки класса, выделение частей и демонстрация преобразований помогает лучше понять теоретический материал. Сведения, которые необходимо запомнить, выделяются в рамку, понятия выделяются ярким цветом. Все это помогает удерживать внимание ученика на предмете изучения и способствует повышению эффективности урока.
Демонстрация начинается с представления вопросов, на которые ученикам следует дать ответ перед изучением темы. Необходимо вспомнить, что является углом между прямой и плоскостью, как изображается наклонная и плоскость, какие приемы решения задач уже известны ученикам, а также насколько важны полученные знания и навыки для успешной сдачи ЕГЭ.
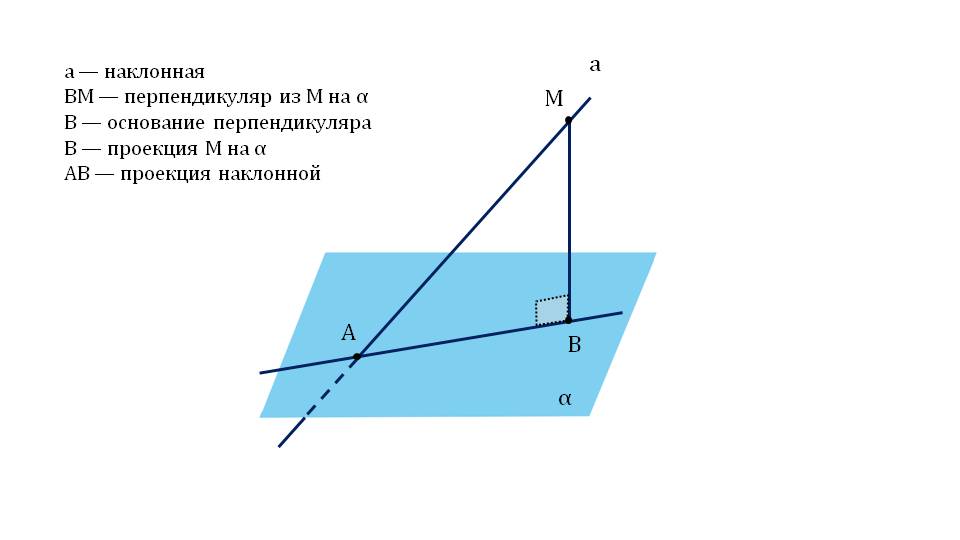
На следующем слайде производится построение наклонной к плоскости α из точки М. Для этого сначала изображается плоскость α в виде закрашенной области экрана, к ней проводится наклонная, на которой отмечается точка М. Затем из точки М опускается перпендикуляр на плоскость, имеющий основание в точке В. Отмечается, что перпендикуляр образует с плоскостью угол 90°. Из точки В строится прямая ВА, которая принадлежит плоскости и, соответственно, перпендикулярна МВ. Данная прямая пересекает наклонную в точке А. Рядом с рисунком отображаются названия элементов, образованных в результате построения – наклонная а, перпендикуляр ВМ, его основание и проекция точки М – точка В, проекция АВ наклонной.
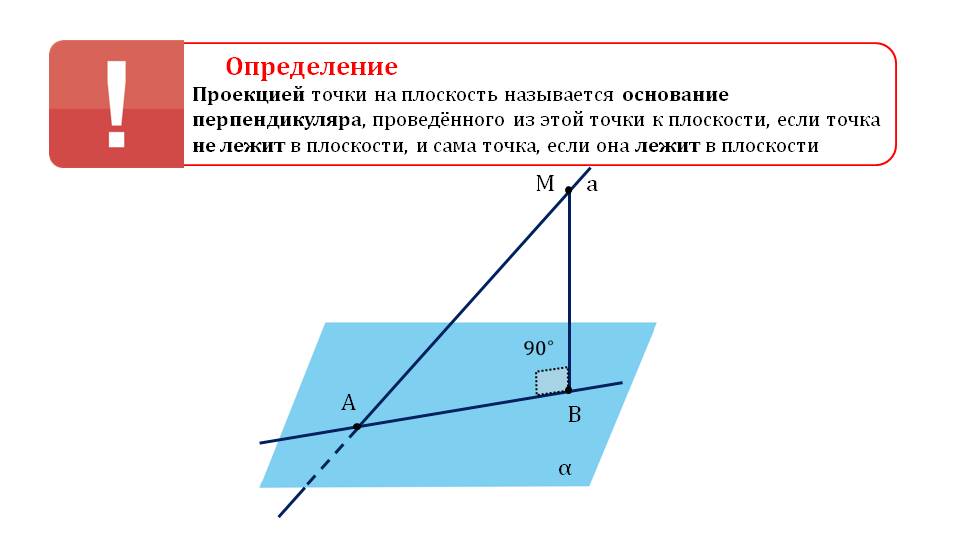

Далее представляется определение проекции точки, отображенной на плоскости как основание перпендикуляра, опущенного на эту плоскость. Также в определении отмечено, если точка отмечена на плоскости, она является проекцией себя на этой плоскости. Далее доказывается теорема, утверждающая, если прямая перпендикулярна плоскости, то ее проекция представляет собой прямую.
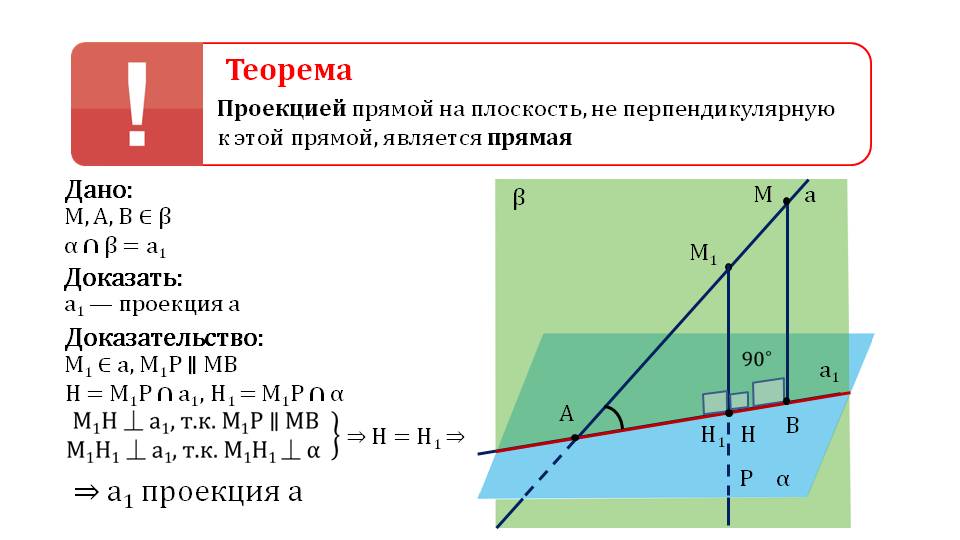
Доказательство начинается с соответствующего построения. К плоскости α строится наклонная а. От ее точки М проведен перпендикуляр к плоскости – МВ, а также проекция наклонной - АВ. Отмечается, что все три точки А, М, В располагаются на плоскости β. При этом данные плоскости α, β пересекаются по некоторой прямой а1. Необходимо доказать, что прямая а1 и является проекцией а. Для этого достраивается дополнительно точка М1, из которой строится прямая, параллельная МВ. При этом прямая М1Р пересекает прямую a в точке Н, а плоскость α пересекает в точке Н1. Построенный М1Н перпендикулярен прямой а1, так как М1Р параллельна МВ, а М1Н1 перпендикулярна а1, так как М1Н1 перпендикулярен плоскости α. Соответственно, точки Н и Н1 совпадают. Поэтому а1 совпадает с проекцией наклонной а.
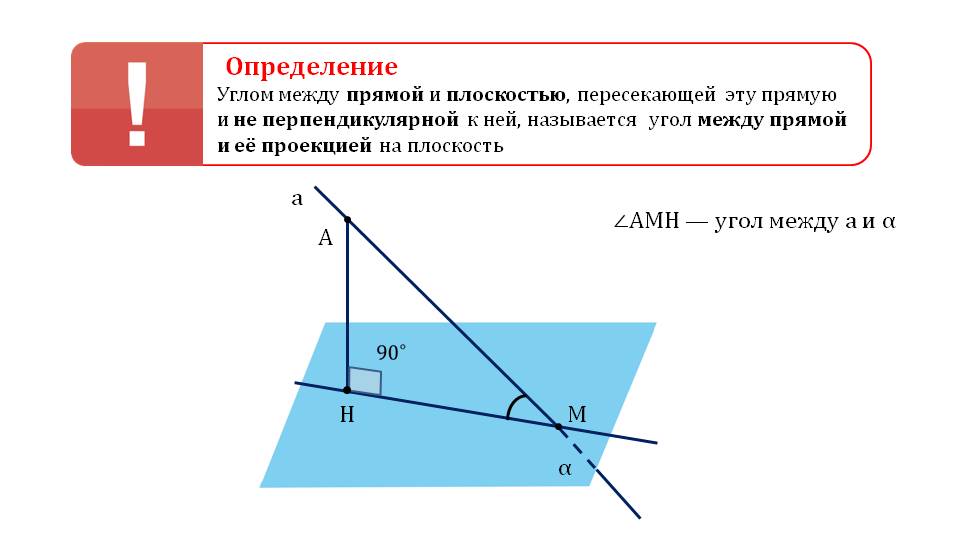
Далее дается определение угла между некоторой прямой с неперпендикулярной ей плоскостью, пересекающей прямую. Этот угол определяется углом между проекцией прямой исамой прямой.
Представлены важные теоретические выводы, нужные для решения задач по данной теме. Среди них понятие проекции прямой, очерченной на плоскости, отрезка, а также проекции на плоскость перпендикулярного отрезка или прямой. Также отмечается, что угол, образованный между наклонной и ее проекцией имеет наименьшую величину из всех углов, образованных наклонной и прямыми данной плоскости. Напоминается о том, что величина угла, образованного перпендикуляром и плоскостью 90°. Когда прямая параллельна плоскости, проекция является прямой, принадлежащей плоскости и параллельной данной, а угол, образованный плоскостью и прямой, равняется 0°. Также отмечается, что проекция прямой на плоскость – это проекция на эту плоскость всех точек прямой.

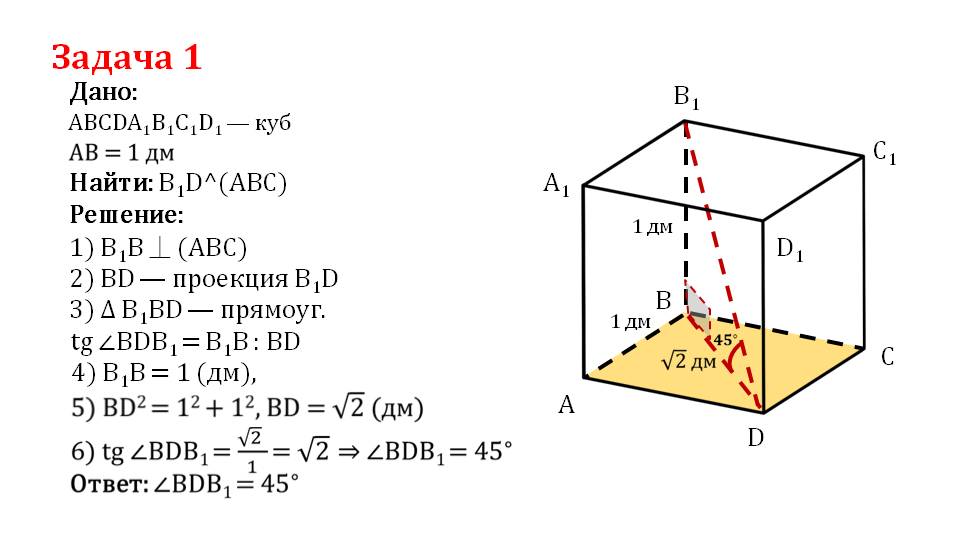
Далее предлагается рассмотреть решение задачи, где условием дан куб ABCDA1B1C1D1 с ребром 1 дм, в котором необходимо найти угол между диагональю куба B1D и его проекцией BD. Решение сопровождается рисунком, на котором изображен рассматриваемый куб, отмечена пунктиром в нем диагональ B1D и диагональ основания BD. Чтобы найти решение, необходимо отметить, что боковые ребра куба перпендикулярны плоскости основания ABCD, а так как BD является проекцией B1D, то образованный при этом треугольник ΔB1BD является прямоугольным. В таком треугольнике тангенс искомого угла ∠B1DB равен отношению B1B/DB. Зная длину ребра куба, можем определить по теореме Пифагора BD=√2 дм. Поэтому tg∠B1DB=√2/1=√2. Отсюда ∠B1DB=45°.
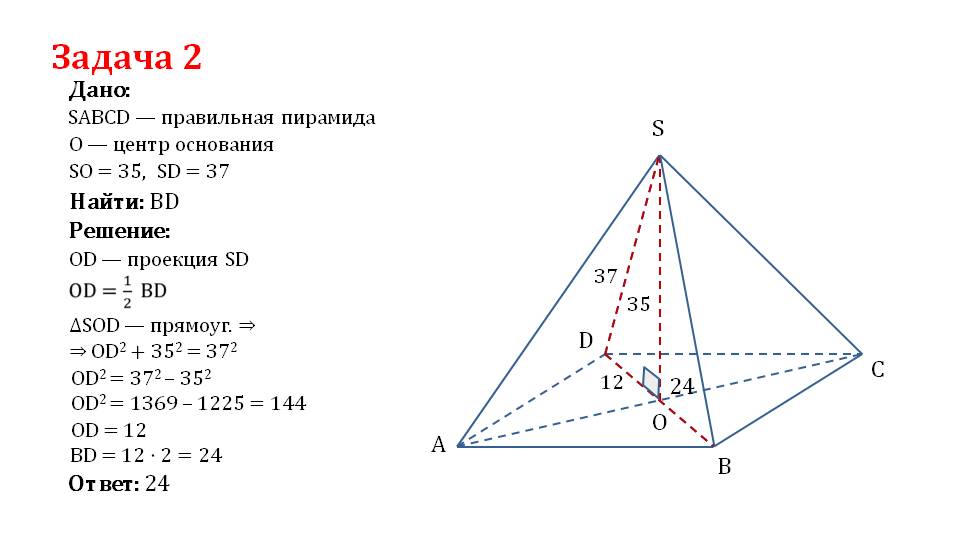
На последнем слайде демонстрируется решение задачи, в которой дана правильная пирамида с центром основания О высотой SO=35 и длиной бокового ребра SD=37. Необходимо найти длину диагонали основания. Задача сопровождается рисунком на котором изображена пирамида ABCDS с отмеченными пунктирной линией диагоналями, и проведенной высотой SO.
Чтобы решить задачу, в пирамиде выделяется красным цветом треугольник, образованный при построении высотой, боковым ребром и половиной диагонали основания. Отмечается, что OD является проекцией наклонной SD и равна половине диагонали DB. Данный треугольник прямоугольный, поэтому для него верно OD2+352=372. Из данного выражения находим OD=144. Так как это половина диагонали, то диагональ BD=12·2=24.
Презентация «Угол между прямой и плоскостью» предназначена для использования на традиционном уроке в школе. Также ее наглядность поможет учителю, осуществляющему дистанционное обучение. Поможет материал освоить решение задач по данной теме и ученикам, которые самостоятельно изучают его.
| Автор | |
|---|---|
| Дата добавления | 28.10.2014 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 15377 |
| Номер материала | 893 |