
Презентация "Умножение одночлена на многочлен"

Краткое описание документа:
Каждому ясно, что математика – это, в первую очередь, цифры и числа. Они преобразовываются впримеры, которые требуют своего решения. Математика необычайно сложная наука, которую понять оченьтрудно, но если человек все-таки понимает, то просто влюбляется в нее, влюбляется в возможностьбороздить в бесконечном потоке цифр и примеров.
В математике существует такие понятия, как одночлен и многочлен.
Одночлен - это простое выражение из двух или нескольких чисел, букв или степеней. И главноеусловие, чтобы произведение чисел и степеней переменной имели натуральные показатели. Так же этолюбое отдельное число, не имеющее буквенных множителей, степень которых равняется нулю.
Многочлен - это выражение, которое является суммой одночленов. Причем многочленом можно назвать иодин одночлен.


слайды 1-2 (Тема презентации "Умножение одночлена на многочлен", пример)
Соответственно между одночленом и многочленом может быть много взаимодействий. Это деление,умножение и сложение. В этом уроке будет рассматриваться умножение одночлена на многочлен.
В этом примере рассматривается тип одночлена, который называется нулевым, поскольку это и такпростое число, его не нужно упрощать.
Это очень просто, если разобраться с каждым числом отдельно.
Одночлен 2a^3 и Многочлен 3a^4-4a^2+a
Чтобы решить эту задачу необходимо одночлен перемножить на каждую составляющую многочлена, исложить полученные результаты .
Это будет выглядеть так
2a^3(3a^4-4a^2+a) = 2a^3∙3a^4-2a^3∙4a^2+2a^3∙a
Теперь более подробно
2a^3∙3a^4 = 6a^7
2a^3∙4a^2 = 8a^5
2a^3∙a = 2a^4
Сложив одночлен с каждым элементом многочлена, получается такая картина:
2a^3 (3a^4-4a^2+a) = 6a^7-8a^5+2a^4
Последний элемент – это уже конечный результат и эти цифры отнимать и плюсовать не нужно. Да это, впринципе, и не возможно, поскольку «а» в них имеют разные степени.

слайды 3-4 (пример, нахождение площади)
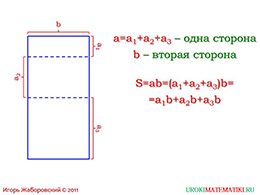
Так же в этом уроке предлагается научиться находить площадь благодаря таким показателям исоответствующему рисунку ниже
a=a1+a2+a3 – одна сторона
b – вторая сторона
А чтобы найти площадь нужно использовать формулу
S=a*b=(a1+a2+a3)b = a1*b+a2*b+a3*b
Несколькими словами эту формулу можно объяснить , как площадь равно произведение одной стороны надругую. Ясно, что сторона «а» равна сумме трех чисел и если «а» складывается из 3 частей, а «b» этопросто «b», то «ab» равно сумме этих кусочков перемноженных на «b»
Необходимо решить пример. Требуется умножить одночлен -3xy на многочлен 2x^2*y+4xy^2-1
Стоит обратить внимание на то, что в этом примере одночлен стоит в отрицательной форме.Соответственно, полученный результат тоже будет иметь отрицательную форму. Пример будет иметь такоерешение:
-3xy∙(2x^2y+4xy^2-1) = -3xy∙2x^2y+(-3xy)∙4xy^2+(-3xy)∙(-1)
В итоге, получается -3xy∙(2x^2*y+4xy^2-1)= -6x^3*y^2-12x^2*y^3+3xy
Здесь тоже понятно, что с конечным результатом тоже ничего не нужно делать из-за разных степеней.

слайд 5 (пример)
Далее предлагается следующий пример. Он заключается в упрощении выражения.
Тип одночлена, который можно упростить называется стандартным.
Имеется 4a(2a+5)+2a(3a-1)-1,5a(2a-4)
Данный пример будет решаться таким способом.
4a(2a+5) +2a(3a-1)-1,5a(2a-4) = 8a^2+20a+6a^2-2a-3a^2+6a = 11a^2+24a
То есть, сначала необходимо открыть скобки, а то, что равняет и является результатом. Затем нужноразобрать очень непростой момент этого примера, который не все с первого раза понимают. Имеется ввиду то, что именно эти самые слагаемые, у которых «а» имеет одинаковую степень, например 8a^2 , 6a^2и 3a^2 можно суммировать или отнимать. В этом случае это 8a^2+6a^2-3a^2
Из всего этого получаются такие действия
8+6=11
20-2+6=24
Отсюда и выходит
11a^2+24a
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Презентация |
| Просмотров | 3985 |
| Номер материала | 187 |