
Урок "Стандартный вид многочлена"

Краткое описание документа:
Члены многочлена являются базовыми единицами многих алгебраических структур. По своему определению, мономы – это либо натуральные числовые значения, либо некие переменные (группы умноженных друг на друга переменных).
Одним из главных математических действий над многочленом является приведение подобных слагаемых. В этом видеоуроке мы рассмотрим более подробно, что собой представляют операции над многочленом.
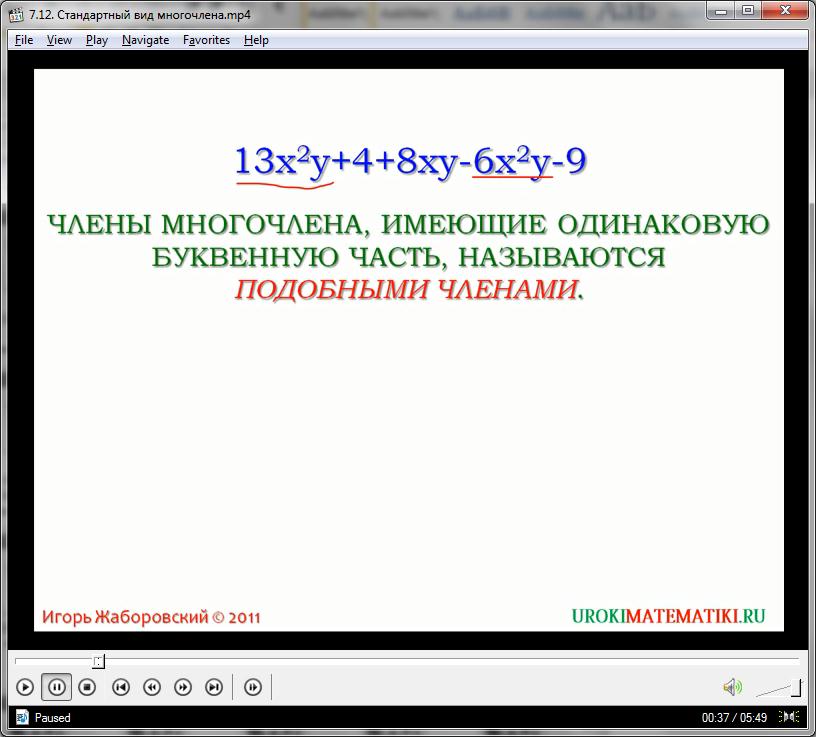
Так как все члены полинома между собой связаны посредством алгебраического суммирования, то все они именуются слагаемыми. Подобными же являются мономы, имеющие одинаковую буквенную часть, т.е. состоящие из одинаковых переменных. При этом переменные обязательно должны быть в одинаковой степени и при равном числовом коэффициенте. А отдельные числовые значения в многочленах считаются приравненными к подобным слагаемым сами по себе.
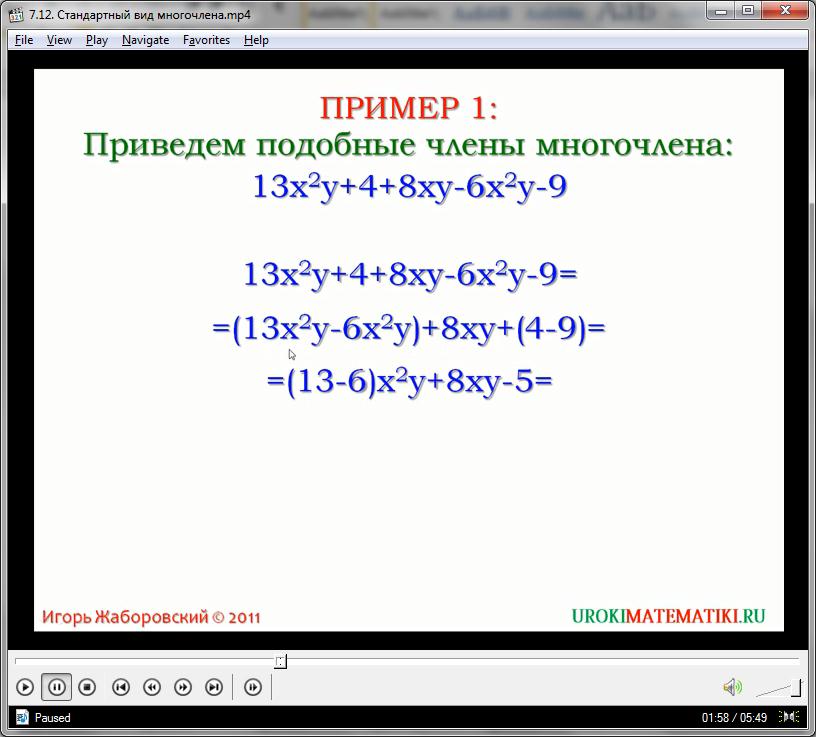
Приведение подобных слагаемых подразумевает группирование мономов многочлена так, чтобы получились отдельные части, состоящие полностью из подобных слагаемых. К примеру, рассмотрим данный многочлен:
3а2 + 2ab2 – 6 – 3с3 + 6а2 - 7ab2 + 7
Подобными слагаемыми, в данном случае, являются:
- Все свободные числовые значения: -6, +7;
- Мономы с основанием а в квадрате: +3а2, +6а2;
- Мономы с основанием аb в квадрате: 2ab2, -7ab2;
- Мономы с основанием с в кубе: -3с3;
Последняя группа состоит из одного лишь одночлена, не имеющего подобного себе во всем полиноме.
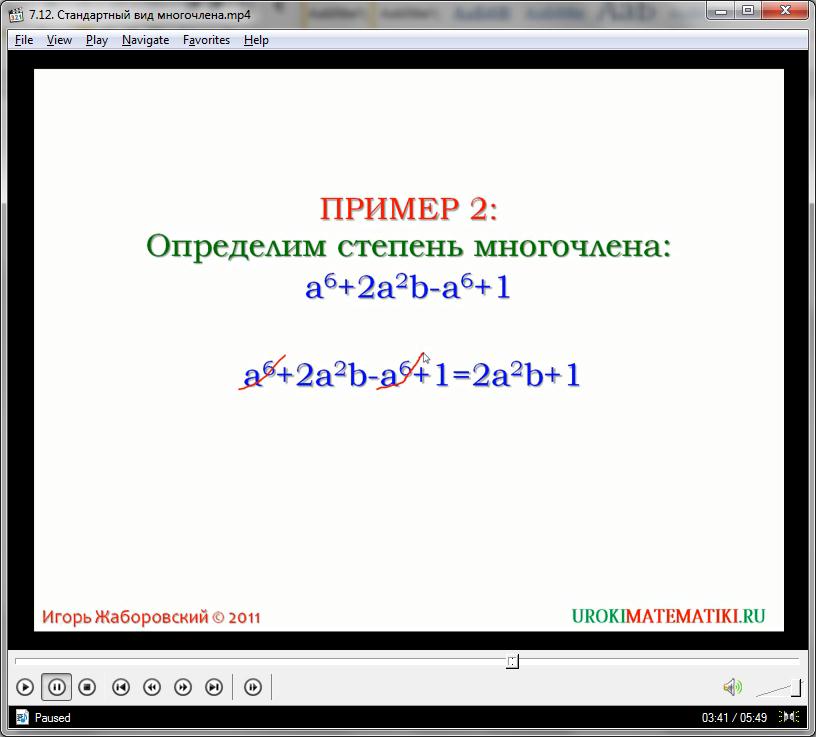
Зачем нужны такие преобразования? Приведение подобных слагаемых помогает упростить многочлен, привести его к элементарному виду, который состоит из меньшего количества мономов. Это легко сделать, сгруппировав те члены, между которыми совершаются алгебраические действия. Главными операциями тут становится вычитание и сложение – они же оказывают эффект перегруппировки и позволяют свободно перемещать одночлены внутри полинома. Поэтому вполне по правилам будет преобразовать вышеуказанный пример так:
-6 +7 + 3а2 +6а2 + 2ab2 +(-7ab2) + (-3с3) =
= 9а2 – 5ab2 – 3с3 – 1
Реализовав стандартное вычитание и сложение, получаем упрощенный многочлен. Если первоначальный вариант насчитывал 7 одночленов, то текущий имеет всего 4 члена. Однако возникает закономерный вопрос, что является точным критерием «простоты» многочлена?
С точки зрения алгебраических правил, элементарным, а точнее – стандартным многочленом считается такой полином, у которого все основания одночленов разные, и не являются подобными друг другу. Наш пример:
9а2 – 5ab2 – 3с3 – 1
Состоит из мономов с основаниями а2, ab2, с3, а также, из одного числового значения. Ни один из вышеперечисленных элементов не может быть суммирован или вычтен из другого. Перед нами – стандартный полином, состоящий из четырех членов.
У любого многочлена есть такой критерий, как степень. Степенью полинома, в общем отношении, называется наибольшая степень одночлена в данном многочлене. Стоит усвоить важную деталь – степени многобуквенных (многопеременных) выражений суммируются. Поэтому, общая степень ab2 равна трем (а в первой степени, b в квадрате). А многочлен вида:
9а2 – 5ab2 – 3с3 – 1
имеет степень, равную трем, так как один из одночленов находится в наибольшей кубической степени.
Степень полиномов принято определять только для стандартного вида. Если многочлен имеет подобные слагаемые, то его сначала приводят к упрощенному виду, а потом вычисляют итоговую степень.
Если многочлен состоит только из одних числовых одночленов, то его стандартная форма приобретает вид единственного числа, являющегося алгебраической суммой всех мономов. Степень данного числа, как многочлена, равна нулю. Если же само число, будучи стандартным видом полинома, приобретает значение «ноль», то его степень считается неопределенной, а сам «нулевой» многочлен называется нуль-полиномом.
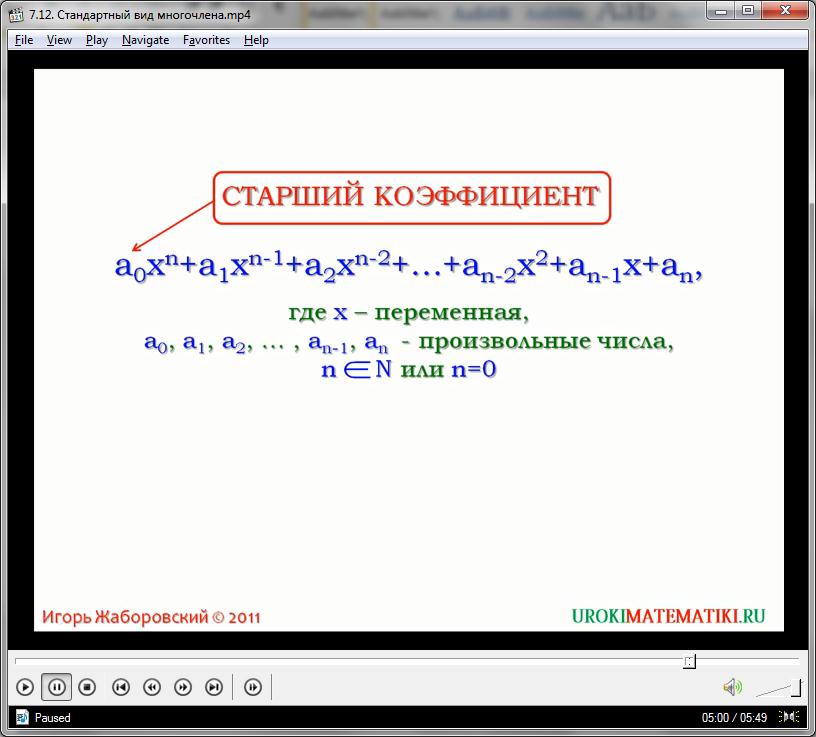
На представленном видео также заметно, что любой многочлен имеет, помимо всего прочего, старший коэффициент и свободный член. Старшим коэффициентом называют числовое значение, стоящие перед переменной с наибольшей степенью (той самой, которая задает разряд самому многочлену). А свободный член – это итоговая сумма всех числовых значений многочлена. Если подобных значений в полиноме нет, либо же если они полностью сокращаются, то свободный член принимают равным 0. В примере:
7а4 – 2в2 + 5с3 + 3
старшим коэффициентом является число 7, потому что оно стоит перед переменной, имеющей наибольшую степень (четвертую – и, вместе с тем, весь многочлен имеет четвертую степень). Свободный член, в данном примере, равен 3.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 6369 |
| Номер материала | 486 |