
Урок "Тождества"

Краткое описание документа:
При изучении математики часто можем наблюдать равенство двух выражений, содержащих арифметические действия. Рассмотрим два таких равенства. Произведение aв двенадцатой степени на a в пятой степени равно произведению a в восьмой степени на a в девятой степени. И частное a в двенадцатой степени, и а в четвертой степени равно произведению a во второй степени на a в шестой степени.
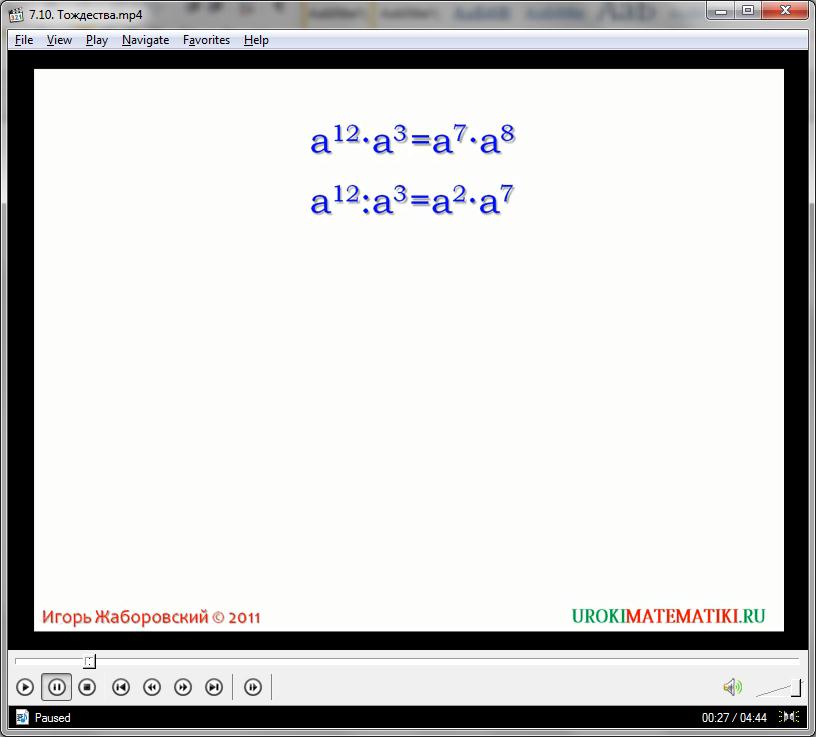
Первое равенство будет выполняться для любых значениях а, потому что aв двенадцатой степени умноженное на a в пятой степени равно a в семнадцатой степени, и a в восьмой степени умноженное на a в девятой степени тоже равно a в семнадцатой степени.
В свою очередь, второе равенство также выполняется при всех значениях переменной aкроме случая, когда a равно нулю. В левой части равенства частное a в двенадцатой степени и а в третьей степени равно a в девятой степени, в правой –произведение aво второй степени на a в седьмой степени тоже равно a в девятой степени. Но в левой части равенства делится на a в степени три. При a равно нулю мы получаем действие с нулем, а на него делить нельзя.
В первом случае возможными значениями переменной a представляет собой множество всех чисел. В равенстве номер два областью всех допустимых для нас значений переменной a для левой части равенства будет множество всех чисел за исключением нуля, а для правой его части – все числа. То есть область допустимых значений для этого равенства будут любые числа, исключая нуль.
Оба рассмотренных нами равенства выполняются для всех допустимых значениях переменной. Тождествами называют верные равенства при всех допустимых значениях переменных. Значит, наши равенства так же будут тождествами.
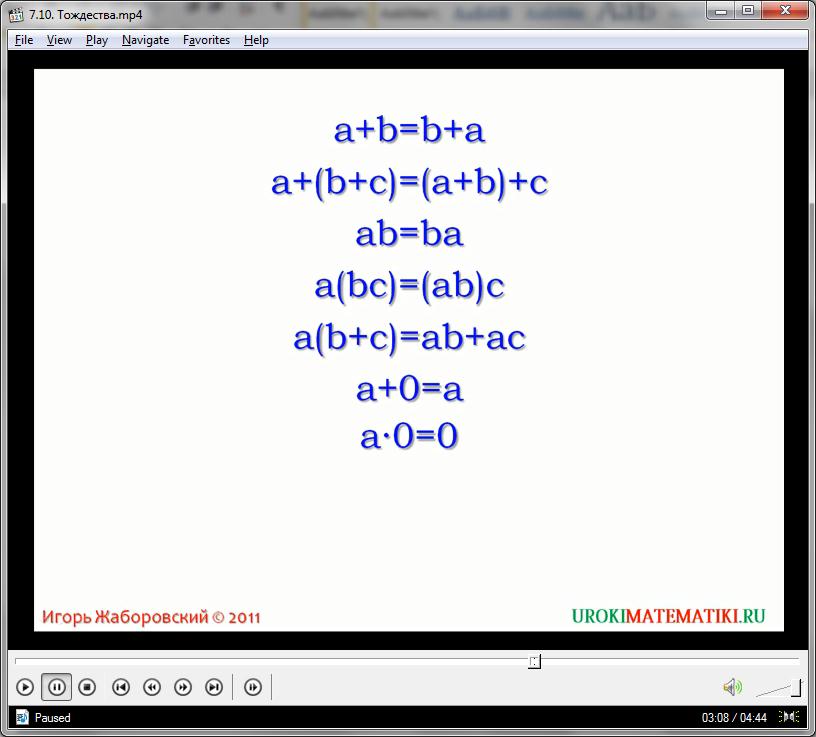
Если числовые равенства верные всегда, то тоже называются тождествами.
С примерами тождеств ранее вам приходилось уже встречаться. Равенства, которые выражают свойства чисел, тоже будут тождествами. Например, свойство сложения, которое мы знаем как переместительное, записанное равенством a + b = b + a. Оно выполняется при всех допустимых значениях переменных a и b. Так же, еще одним примером служит запись другого свойства сложения чисел - сочетательного a + (b + c) = (a + b) + c. Возможна и запись переместительного, сочетательного, распределительного свойств умножения чисел: ab = ba, a(bc) = (ab)c, a(b + c) = ab + ac. Есть тождествами и равенства a + 0 = a, a 0 = 0, a 1 = a, a (-1) = -a.
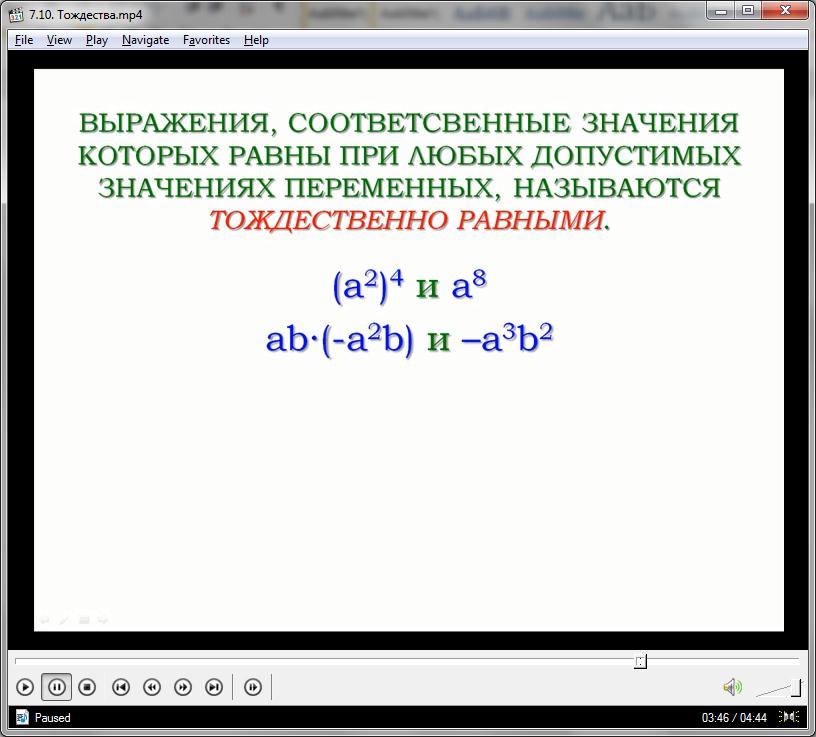
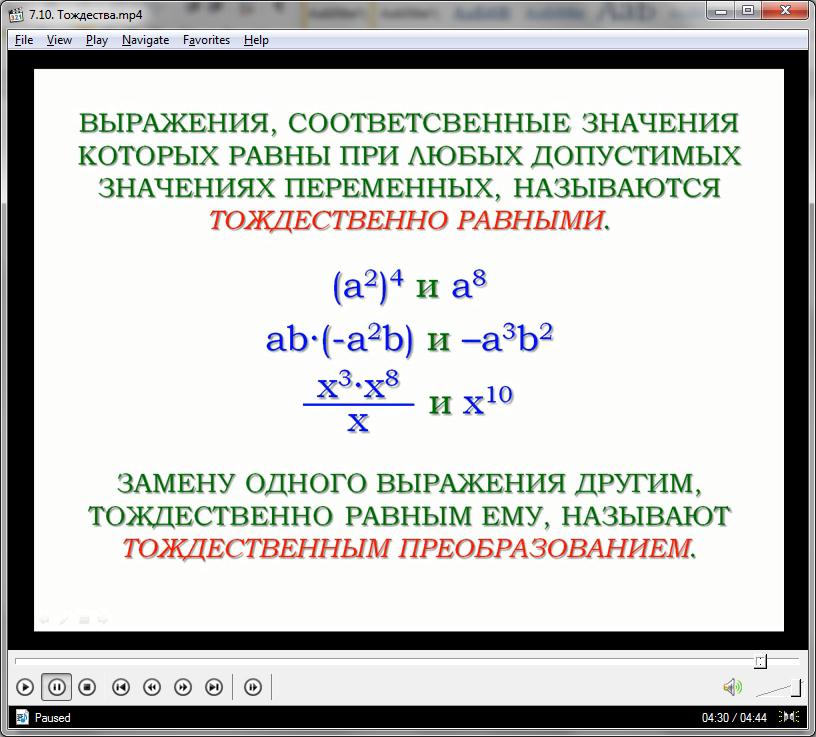
Существует понятие «выражения тождественно равные». Выражения тождественно равными называют те, у которых соответствующие значения равны при любых допустимых значениях переменных. Примерами таких выражений могут служить a в квадрате в четвертой степени и a в восьмой степени, а также произведение a на b, умноженное на произведение минус a в квадрате на b и произведение минус a в кубе на b в квадрате. Это объясняется тем, что после выполнения возможных действий в этих выражениях мы получим абсолютно одинаковые выражения.
Знания о тождественных выражениях нужны для выполнения тождественных преобразований, упрощающих решения многих трудных задач. Тождественные преобразования – это и есть замена одного выражения тождественно равным ему выражением. Тождественные преобразования выполнялись при решении уравнений, умножении одночленов, умножении многочлена на одночлен и многочлена на многочлен.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 3589 |
| Номер материала | 484 |