
Урок "Многочлен. Вычисление значений многочленов"

Краткое описание документа:
Многочлен (иначе именуемый полиномом) представляет собой алгебраическую сумму двух и более одночленов. Стоит пояснить, что представляет собой элементарный одночлен. Моном (одночлен) – это базовая алгебраическая конструкция, представляющая собой некую переменную в положительной степени, имеющую числовой коэффициент (который может быть отрицательным или положительным). При этом коэффициент при переменной может быть равен единице – тогда одночленом является сама переменная, задаваемая, чаще всего, латинскими буквами от конца алфавита – x, y, z.
С другой стороны, часто встречаются примеры одночленов из одного лишь числового коэффициента. Некоторые старые руководства по математике гласят, что одночлен – это алгебраическое выражение, не содержащее знаков суммирования или вычитания. При этом умножение и дробь могут быть в одном мономе. Данное определение не столь корректно, но более реально описывает фактические примеры одночленов.
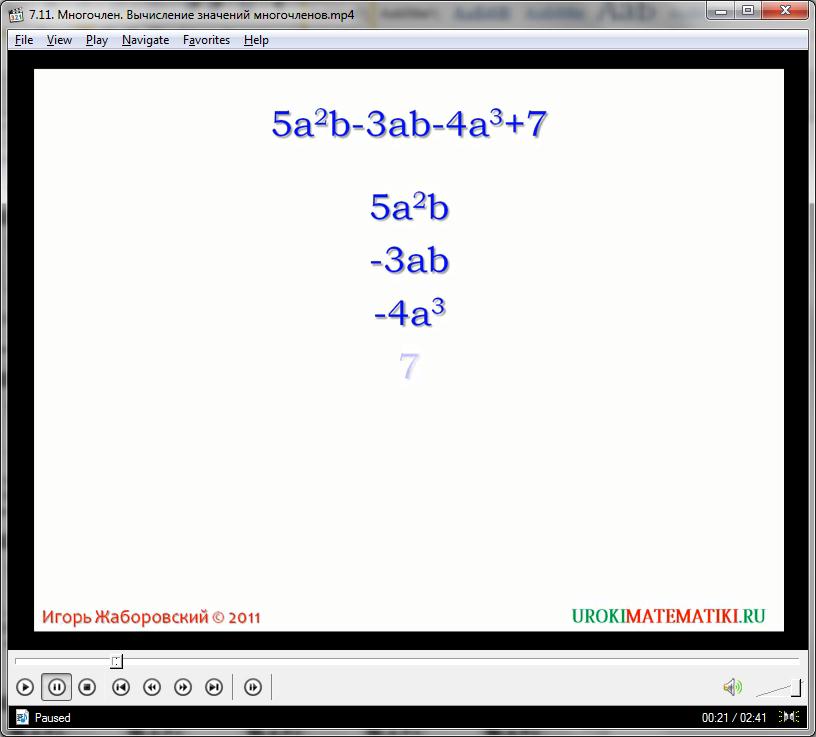
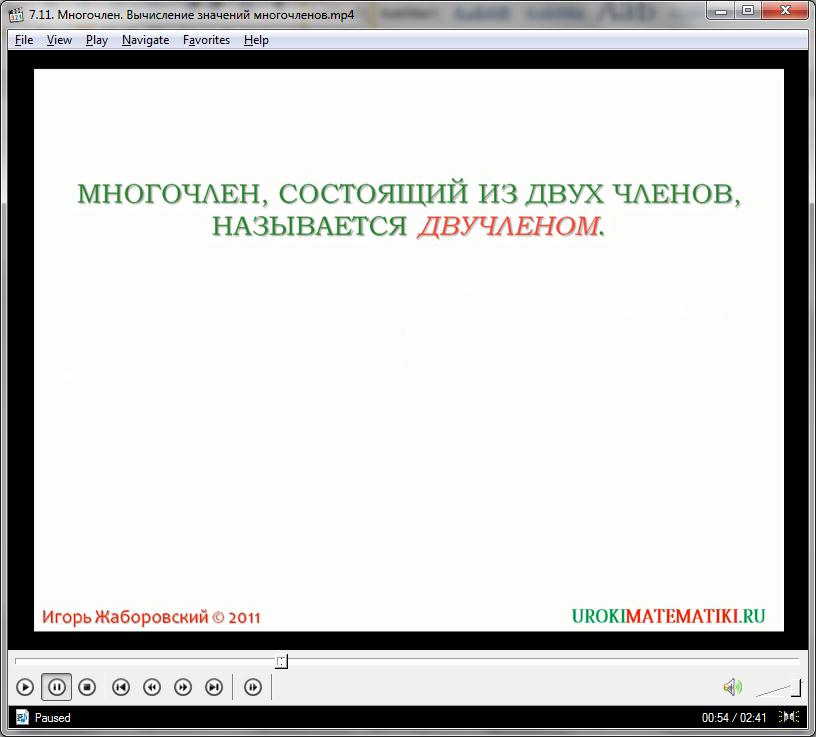
Несколько одночленов образуют многочлены – цепочки алгебраических базовых выражений. Если одночлена два – то образуется бином, если три и больше – то полином. Многочлены являются вторым уровнем элементарных математических выражений, после одночленов.
Важно отметить, что при помощи полиномов не только выстраиваются многочисленные задачи в алгебре, но и производится дальнейшее усложнение простейших математических конструкций. Через понятие «многочлен» выводятся определения для «уравнения» и «алгебраической функции». Поэтому данный видеоурок посвящен работе с многочленами. Быстрое решение задач с их участием позволит лучше усвоить многие смежные темы.
Рассмотрим выражение вида:
3а2 + 4с3 – а2 + 2с3
Данный пример является алгебраическим многочленом, состоящим из четырех различных одночленов. Каждый индивидуальный элемент-моном многочлена носит название «член многочлена». Выражение легко разбивается по знакам сложения и вычитания, образуя четыре отдельных монома:
3а2, 4с3, а2, 2с3
Они в сумме (алгебраической) и дают исходный многочлен. Приравнивание выражения к любому числовому значению или другому полиному образует уравнение, однако, это тема для другого видеоурока.
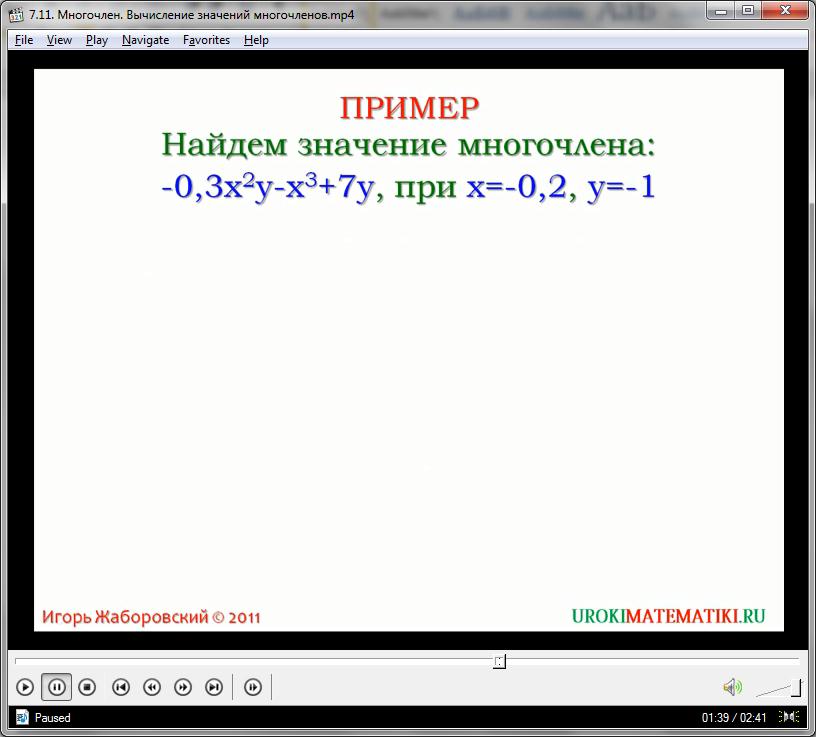
Чтобы найти значение многочлена, следует понимать основные принципы данного процесса. Решением многочлена называется его упрощение – максимальное, реальное математически, уменьшение количества членов выражения. Стоит отметить, что для комплексного решения многих задач необходимо, скорее, уметь привести многочлен в выгодную форму. А она не всегда бывает самым коротким многочленом. Если выражение предназначено для дальнейшей работы – то вид, к которому его необходимо будет привести, должен зависеть от специфики грядущих математических операций.
Чтобы просто решить многочлен, нужно разложить его по отдельным группам, состоящим из подобных алгебраических элементов. Главное требование к этим элементам – возможность быстрого оперирования в пределах своей группы. К примеру, все отдельные числовые значения выносятся в одну группу – действия между ними осуществляются элементарными математическими операциями. Так же легко выделяются одинаковые переменные, квадраты таких переменных и т.д.
Группируя члены полинома стоит помнить правило сохранности знаков «плюс» и «минус» перед выражением. Они являются важнейшим и неотъемлемым атрибутом одночлена, и их потеря приведет к неверным результатам.
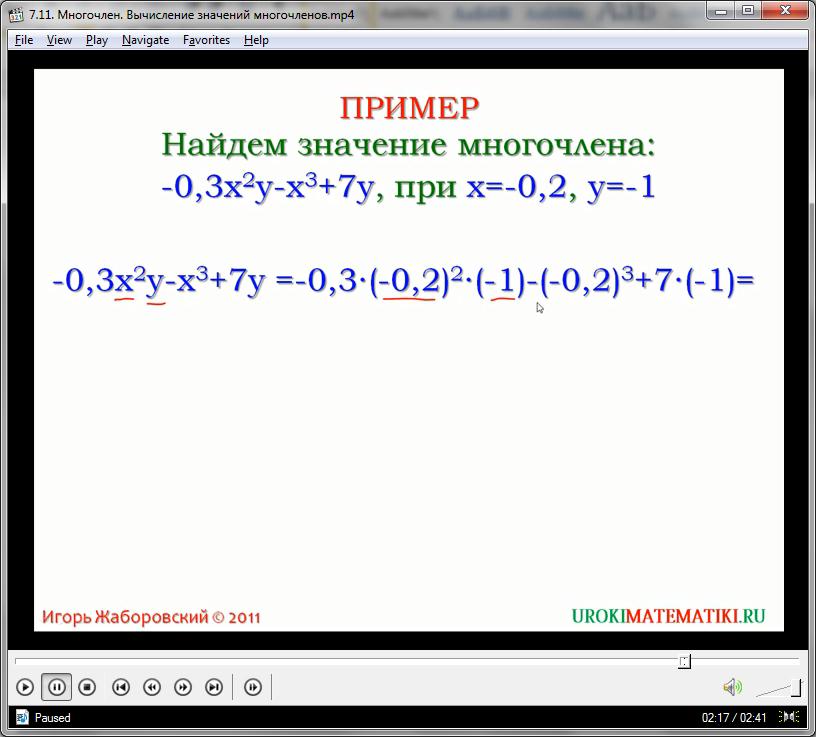
3а2 + 4с3 – а2 + 2с3 = 3а2 - а2 + 4с3 + 2с3 = 2а2 + 6с3
Как видим в нашем уроке, решение многочленов – довольно простая задача, требующая лишь внимательности и точного следования элементарным алгебраическим правилам.
| Автор | |
|---|---|
| Дата добавления | 29.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 8740 |
| Номер материала | 485 |