
Презентация урока геометрии в 10 классе "Перпендикулярность прямых и плоскостей"







Описание презентации по отдельным слайдам:
Урок геометрии в 10 классе по теме «Перпендикулярность прямых и плоскостей» Презентацию составила учитель математики МБОУ «Примокшанская СОШ» Гусарова Т.Д.
1 урок по теме Тема «Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости» Цели: доказать лемму о перпендикулярности двух параллельных прямых к третьей прямой; дать определение прямой, перпендикулярной к плоскости.
. Актуализация знаний. Дано: ABCDA1B1C1D1 – параллелепипед. BAD = 30°. Найдите угол между прямыми АВ и А1D1; А1В1 и AD; АВ и В1С1. BAD = 90°. Докажите, что ВС ┴ B1C1 и AB ┴ A1D1. АDD1 = 90°. Докажите, что AB ┴ C1и DD1 ┴A1B1.
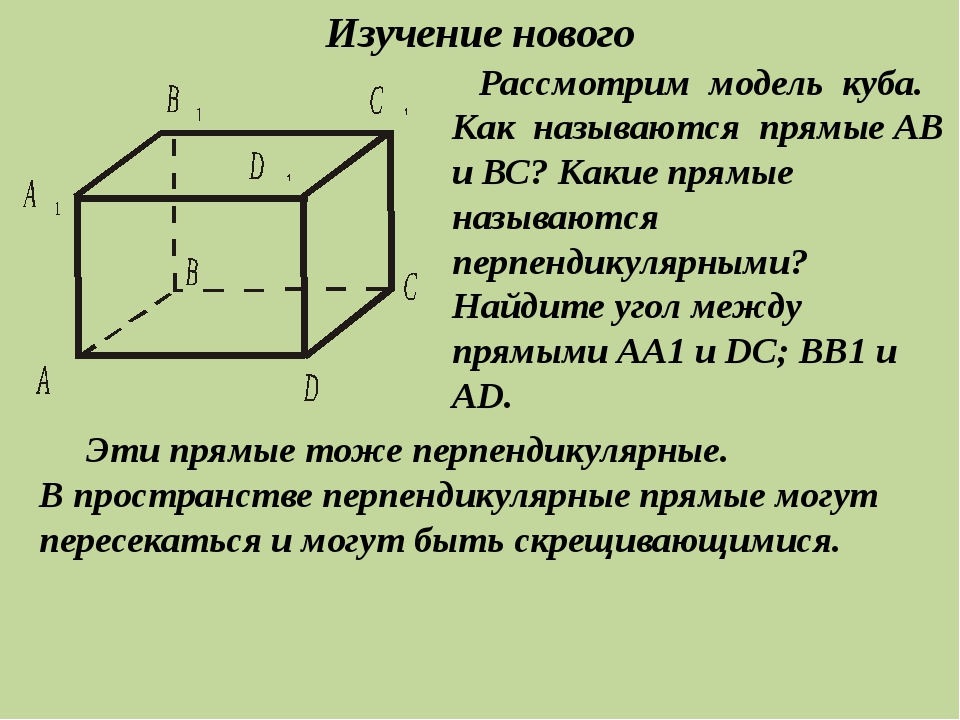
Изучение нового Рассмотрим модель куба. Как называются прямые АВ и ВС? Какие прямые называются перпендикулярными? Найдите угол между прямыми АА1 и DC; ВВ1 и AD. Эти прямые тоже перпендикулярные. В пространстве перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.
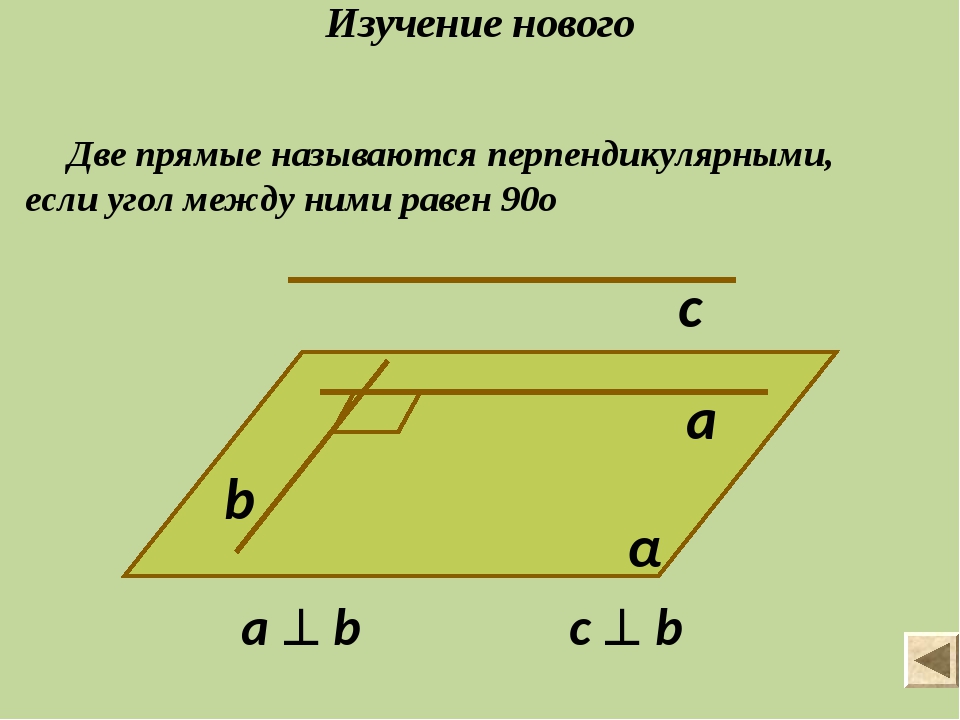
Изучение нового Две прямые называются перпендикулярными, если угол между ними равен 90о а b с а b c b α
Изучение нового Рассмотрим прямые АА1, СС1 и DC. Прямая АА1 параллельна прямой СС1, а прямая СС1 перпендикулярна прямой CD. Нами установлено, что АА1 перпендикулярна CD. Сформулируйте это утверждение.
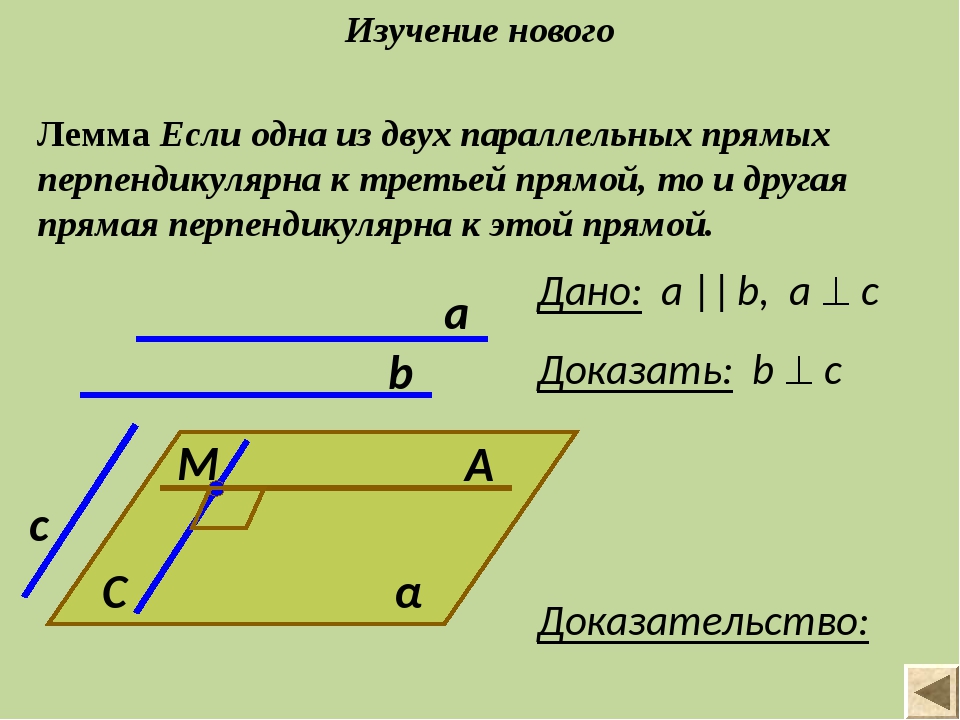
Лемма Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой. A C a α M b c Дано: а || b, a c Доказать: b c Доказательство: Изучение нового
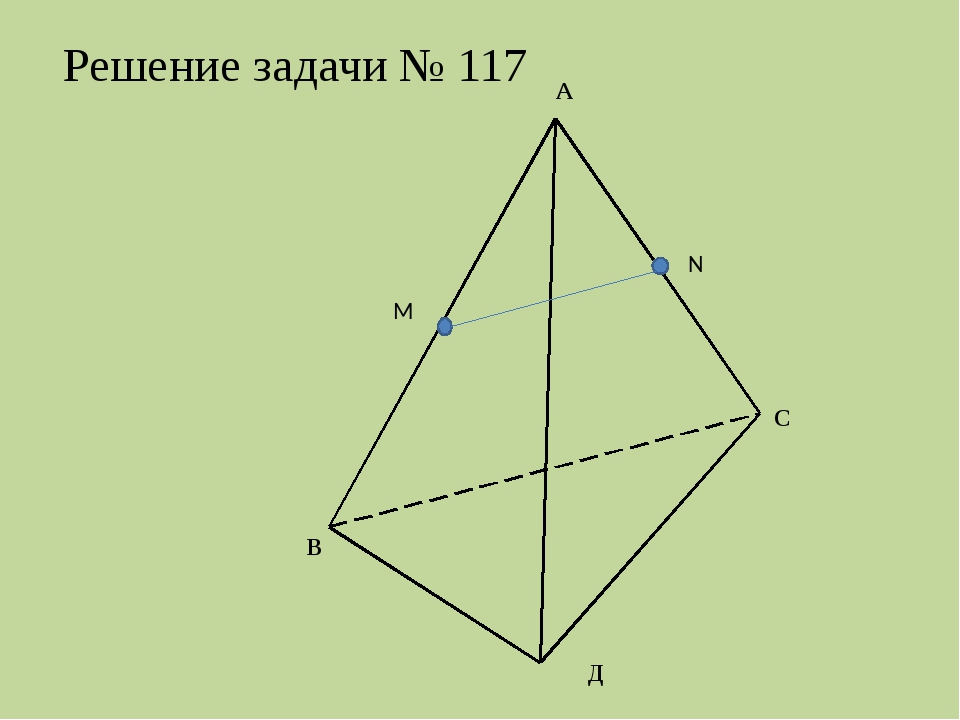
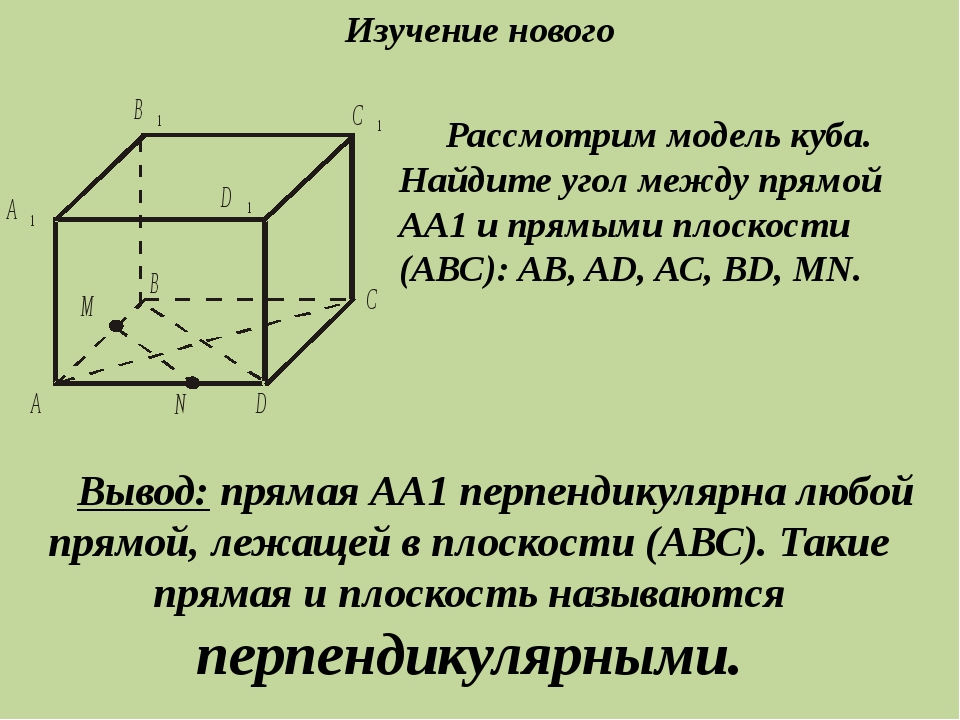
Рассмотрим модель куба. Найдите угол между прямой АА1 и прямыми плоскости (АВС): АВ, AD, АС, BD, MN. Вывод: прямая АА1 перпендикулярна любой прямой, лежащей в плоскости (АВС). Такие прямая и плоскость называются перпендикулярными. Изучение нового
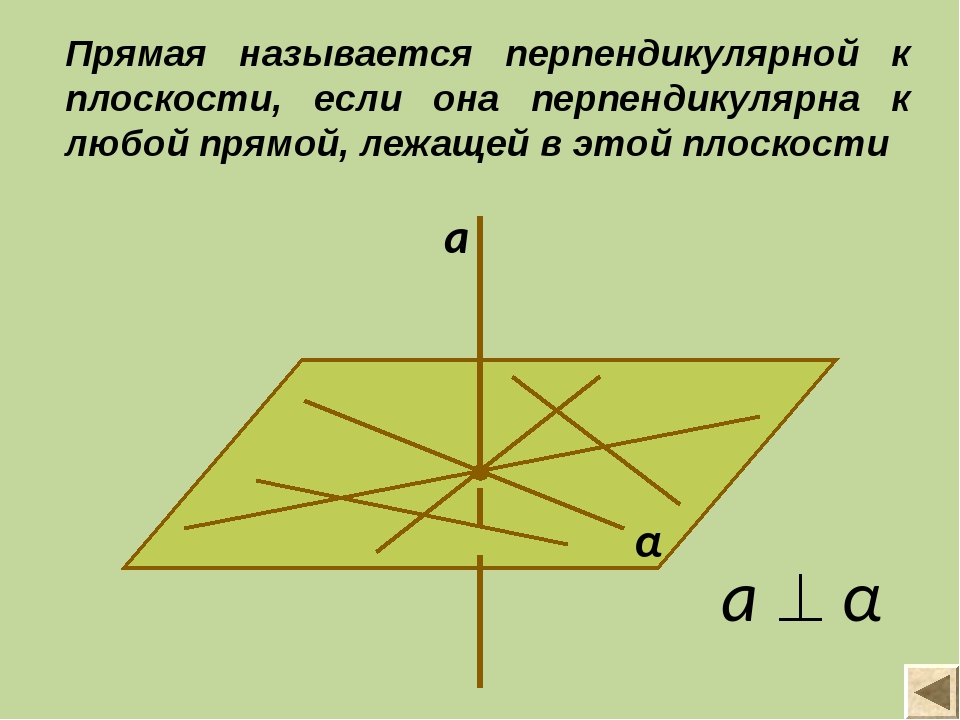
Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости α а а α
Теорема 1 Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости. α х Дано: а || а1; a α Доказать: а1 α Доказательство: a а1
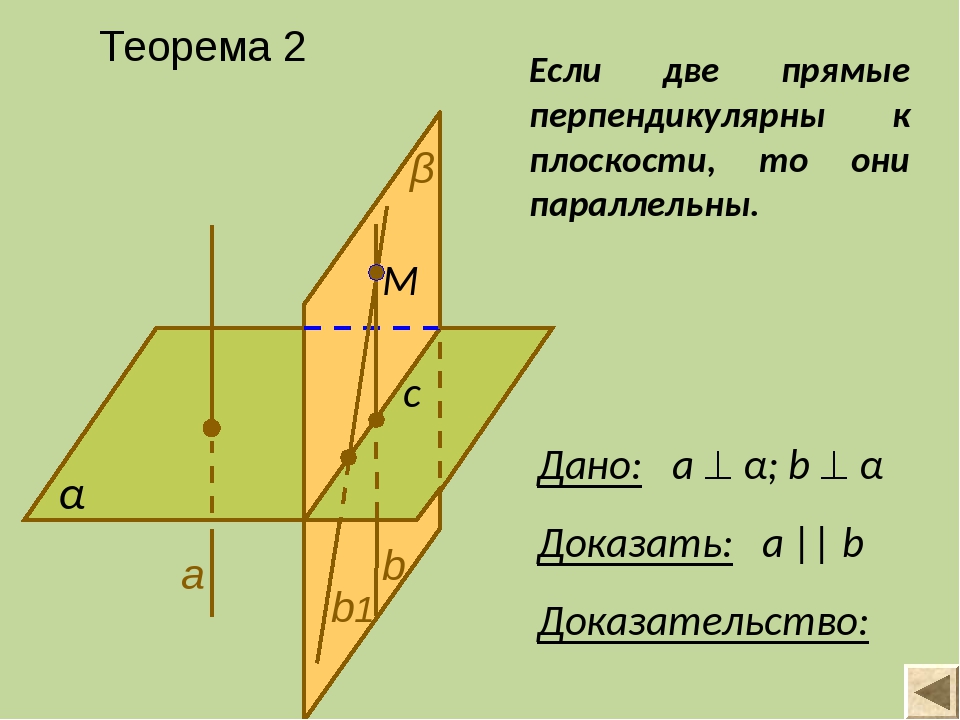
Теорема 2 α Доказать: а || b Доказательство: Если две прямые перпендикулярны к плоскости, то они параллельны. Дано: а α; b α M с a β b1 b
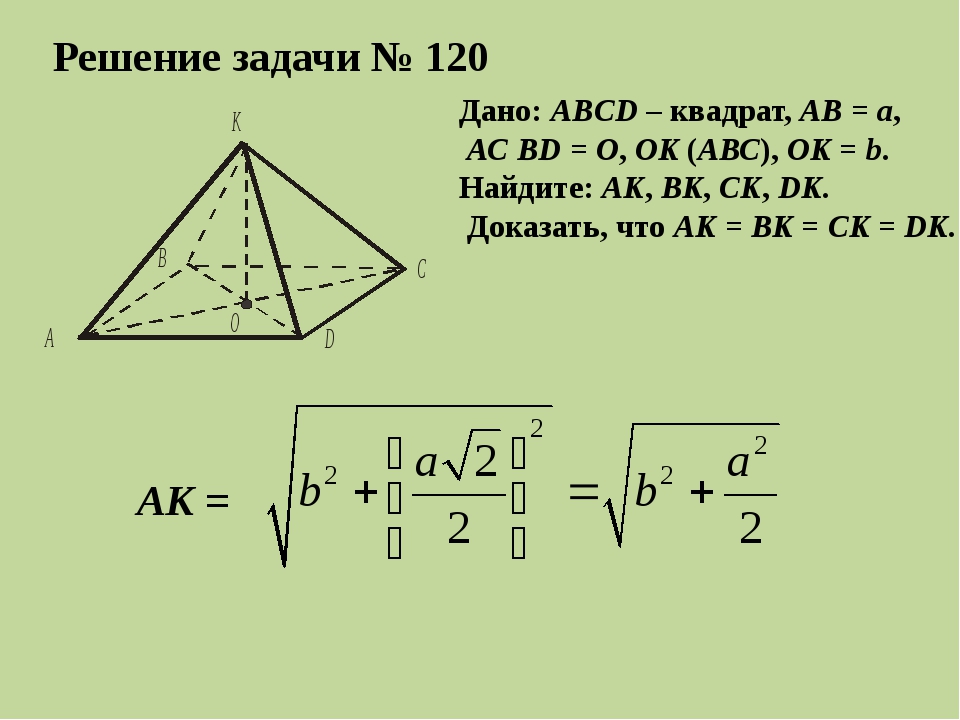
Решение задачи № 120 Дано: ABCD – квадрат, АВ = а, АС BD = О, ОK (АВС), ОK = b. Найдите: АK, ВK, СK, DK. Доказать, что АK = ВK = СK = DK. АК =
Домашнее задание: п. 15, 16, №№ 118, 121. (Указание: медиана, проведенная в прямоугольном треугольнике к гипотенузе, равна ее половине.)

| Автор | |
|---|---|
| Дата добавления | 22.04.2019 |
| Раздел | Геометрия |
| Подраздел | Презентация |
| Просмотров | 3153 |
| Номер материала | 6203 |