
Самостоятельная работа "СБОРНИК УПРАЖНЕНИЙ ПО МАТЕМАТИКЕ"
сборник упражнений по математике
§1. Математические действия
Обратить внимание!
Если в примере есть сложение, вычитание, умножение, деление, то сначала надо сделать умножение и деление, потом сложение и вычитание по порядку.
Обратить выполнение на дроби, которые имеют разные знаменатели ![]() Чтобы сложить (вычесть) дроби с разными знаменателями, надо привести дроби к общему знаменателю, сложить новые числители и написать общий знаменатель.
Чтобы сложить (вычесть) дроби с разными знаменателями, надо привести дроби к общему знаменателю, сложить новые числители и написать общий знаменатель.
Выполните действия:
| 1.1. 1.2. 1.3. 1.4. | 1.5. 1.6. 1.7. 1.8. |
| 1.9. 1.10. 1.11. 1.12. 1.13. | 1.14. 1.15. 1.16. 1.17. 1.18. 1.19. 1.20. 1.21. 1.22. |
1.19. Обратите смешанное число в неправильную дробь:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
1.20. Обратите неправильную дробь в смешанное число:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
§2. Пропорции. Отношения. Уравнения
Помните: Отношение – это частное от деления числа «а» на число «в», не равное нулю, ![]() или а:в – это отношение.
или а:в – это отношение.
Свойство отношения: члены отношения можно умножать или делить на одно и то же число, не равное нулю.
![]()
![]() .
.
Отношение показывает, во сколько раз число «а» больше, чем число «в», или во сколько раз число «в» меньше, чем число «а».
Пропорция – это равенство двух отношений ![]() или
или ![]() - это пропорция.
- это пропорция.
Свойство пропорции: произведение крайних членов пропорции равно произведению средних членов пропорции. ![]()
Уравнения. Для выполнения заданий этого раздела нужно владеть определением (понятием) корня уравнения, уметь решать простейшие уравнения.
Основные формулы. Пусть а,в – числа; х – неизвестный член.
а+х = в, тогда х=в-а
а·х=в, тогда ![]()
![]() , тогда
, тогда ![]()
![]() тогда
тогда ![]()
Найдите х:
| 2.1. 2.4. 2.7. 2.10. 2.13. 2.16. 2.19. | 2.2. 2.5. 2.8. 2.11. 2.14. 2.17. 2.20. | 2.3. 2.6. 2.9. 2.12. 2.15. 2.18. |
§3. Действия со степенями:
Помните основные формулы:
![]() ;
; ![]() ;
;
![]() ;
; ![]()
![]() ;
; ![]()
Выполните действия:
3.1. ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
3.2. ![]() ; 3.3.
; 3.3. ![]() ;
;
3.4.![]() ; 3.5.
; 3.5. ![]()
3.6.![]() ; 3.7.
; 3.7. ![]()
§4. Формулы сокращенного умножения
Повторите формулы сокращенного умножения:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
| 4.1. 4.2. 4.3. 4.4. 4.5. | 4.6. 4.7. 4.8. 4.9. 4.10. |
§5. Алгебраические дроби.
Тождественные преобразования алгебраических выражений.
Для тождественного преобразования дробного выражения – нужно найти область определения этого выражения и потом произвести действия, выбирая наиболее «короткий» путь к верному ответу.
| 5.1. 5.4. 5.7. 5.10. 5.13. | 5.2. 5.5. 5.8. 5.11. 5.14. | 5.3. 5.6. 5.9. 5.12. 5.15. |
§6. Квадратные уравнения.
Для решения квадратных уравнений помните:
1) ![]() ,
, ![]() ,
, ![]() ;
; ![]()
2) ![]() ,
, ![]() ,
, ![]() ;
;
3) ![]() ,
, ![]() , если
, если ![]() .
.
Но если ![]() , уравнение не имеет решения.
, уравнение не имеет решения.
Решите уравнения:
| 6.1. 6.4. 6.7. 6.10. 6.13. | 6.2. 6.5. 6.8. 6.11. 6.14. | 6.3. 6.6. 6.9. 6.12. 6.15. |
§7. Неравенства. Системы неравенств.
Обратите внимание, что при решении линейных неравенств вида ![]() используются основные формулы: пусть а и в – числа; х – неизвестный член и
используются основные формулы: пусть а и в – числа; х – неизвестный член и ![]()
1) ![]() , тогда
, тогда ![]()
2) ![]() , тогда:
, тогда:
если ![]() , тогда
, тогда ![]() ;
;
если ![]() , тогда
, тогда ![]() .
.
3) ![]() , тогда:
, тогда:
если ![]() , тогда
, тогда ![]() ;
;
если ![]() , тогда
, тогда ![]() .
.
При решении систем неравенств помните, что решением системы неравенств является объединение интервалов решений каждого неравенства
Решите неравенства:
| 7.1. 7.4. 7.7. 7.10. 7.13. | 7.2. 7.5. 7.8. 7.11. 7.14. | 7.3. 7.6. 7.9. 7.12. 7.15. |
Решите системы неравенств:
| 7.16. 7.19. 7.22. | 7.17. 7.20. 7.23. | 7.18. 7.21. 7.24. |
§8. Определители. Системы уравнений.
Помните, что определителем второго порядка, составленным из чисел ![]() называется число, определяемое равенством:
называется число, определяемое равенством:
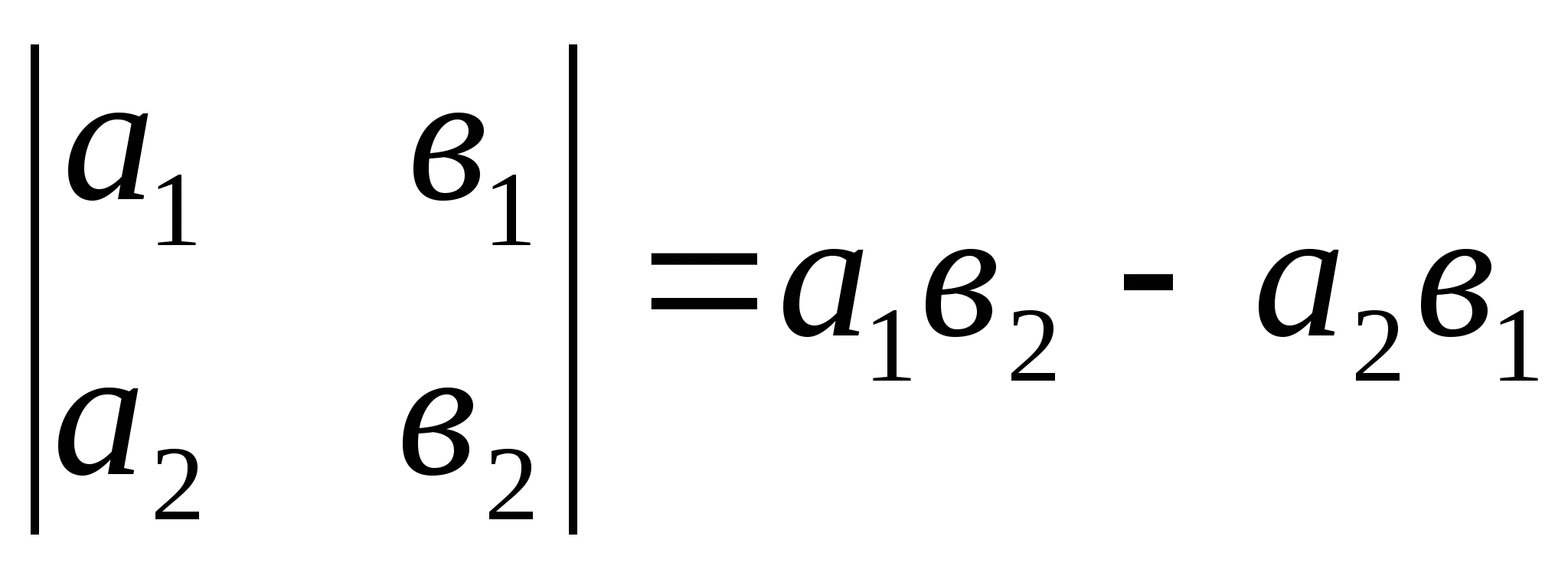 .
.
Чтобы решить систему линейных уравнений с двумя переменными 
Помните формулы Крамера ![]() ,
, ![]() , где
, где
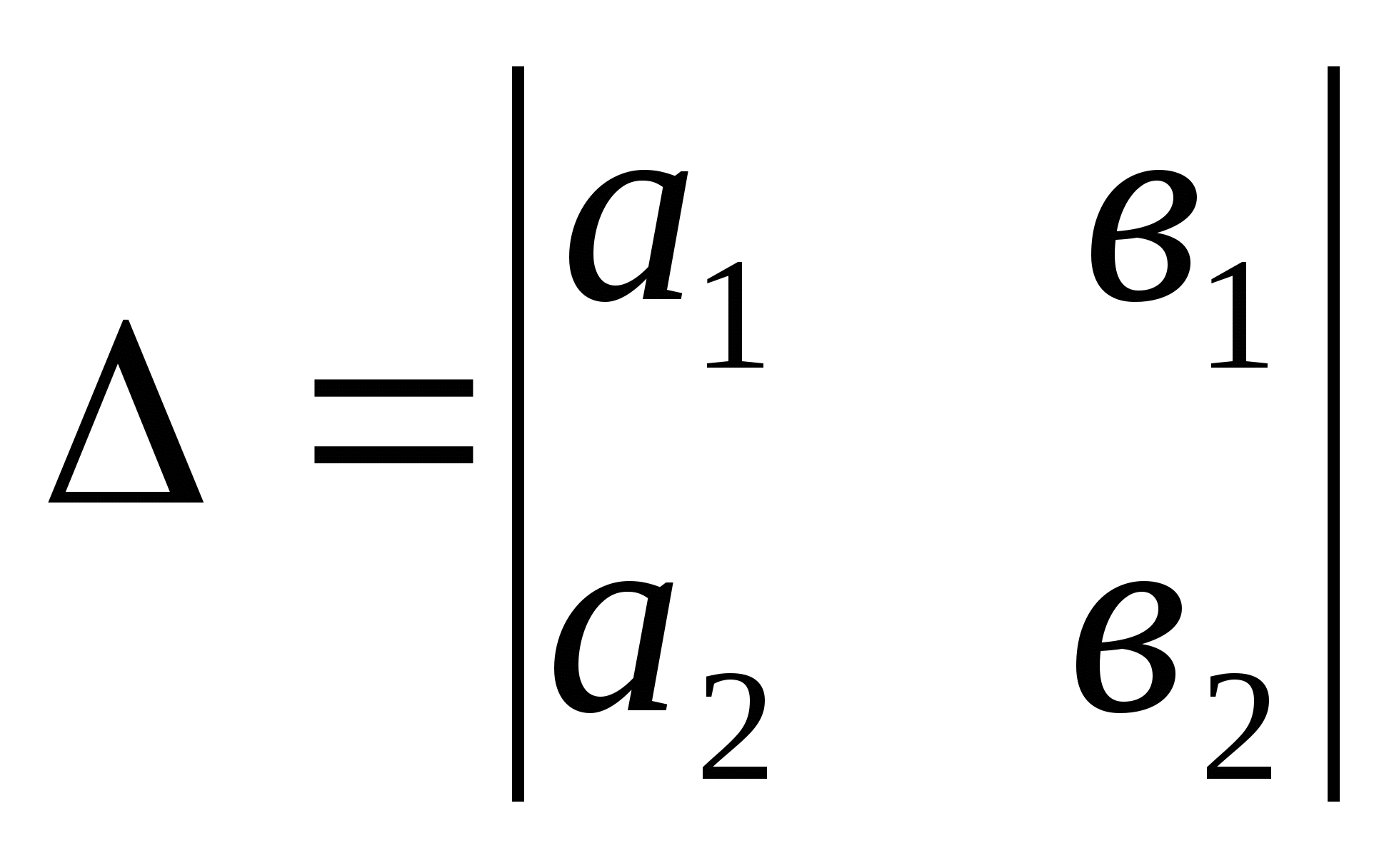 ,
, 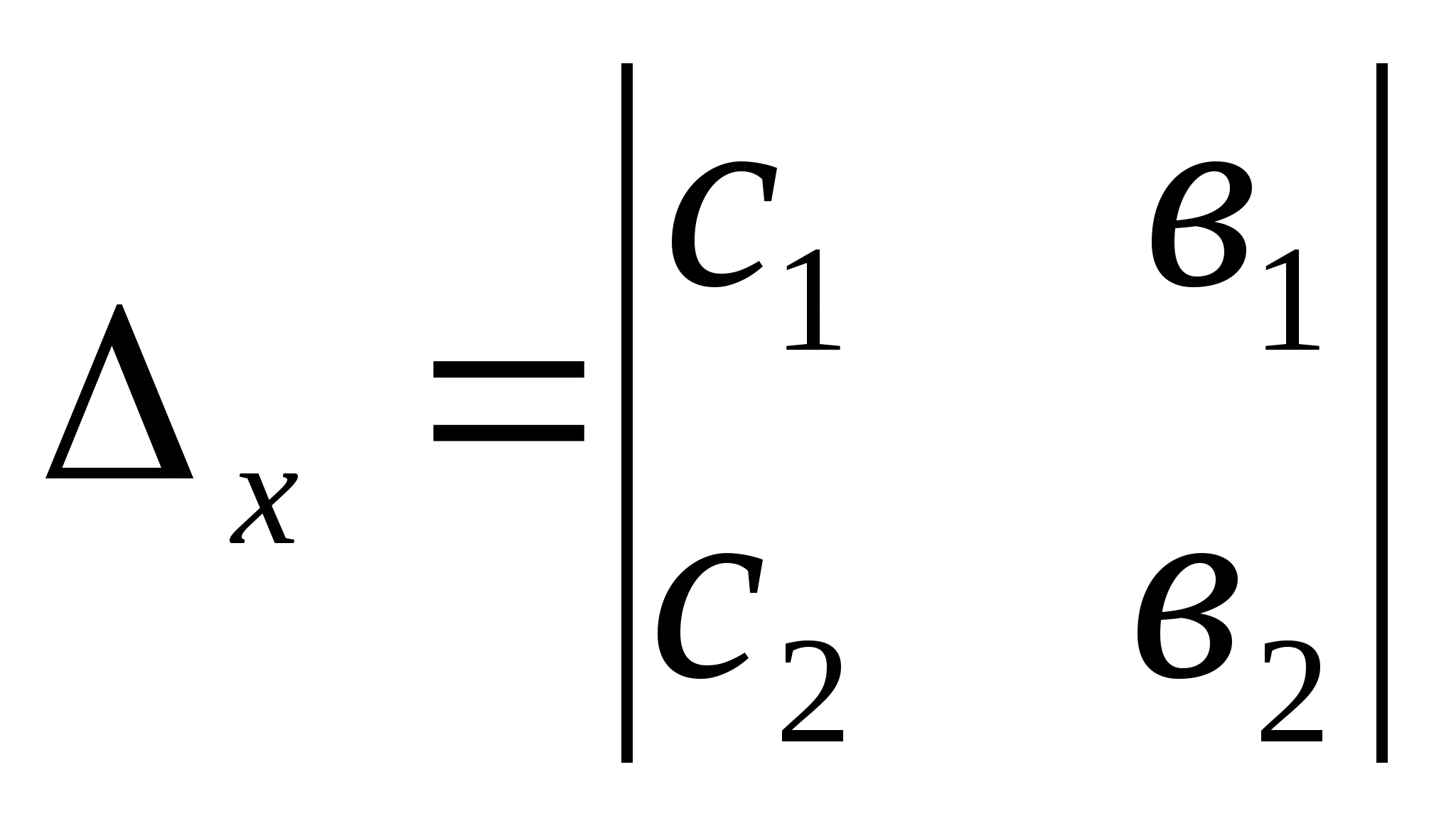 ,
, 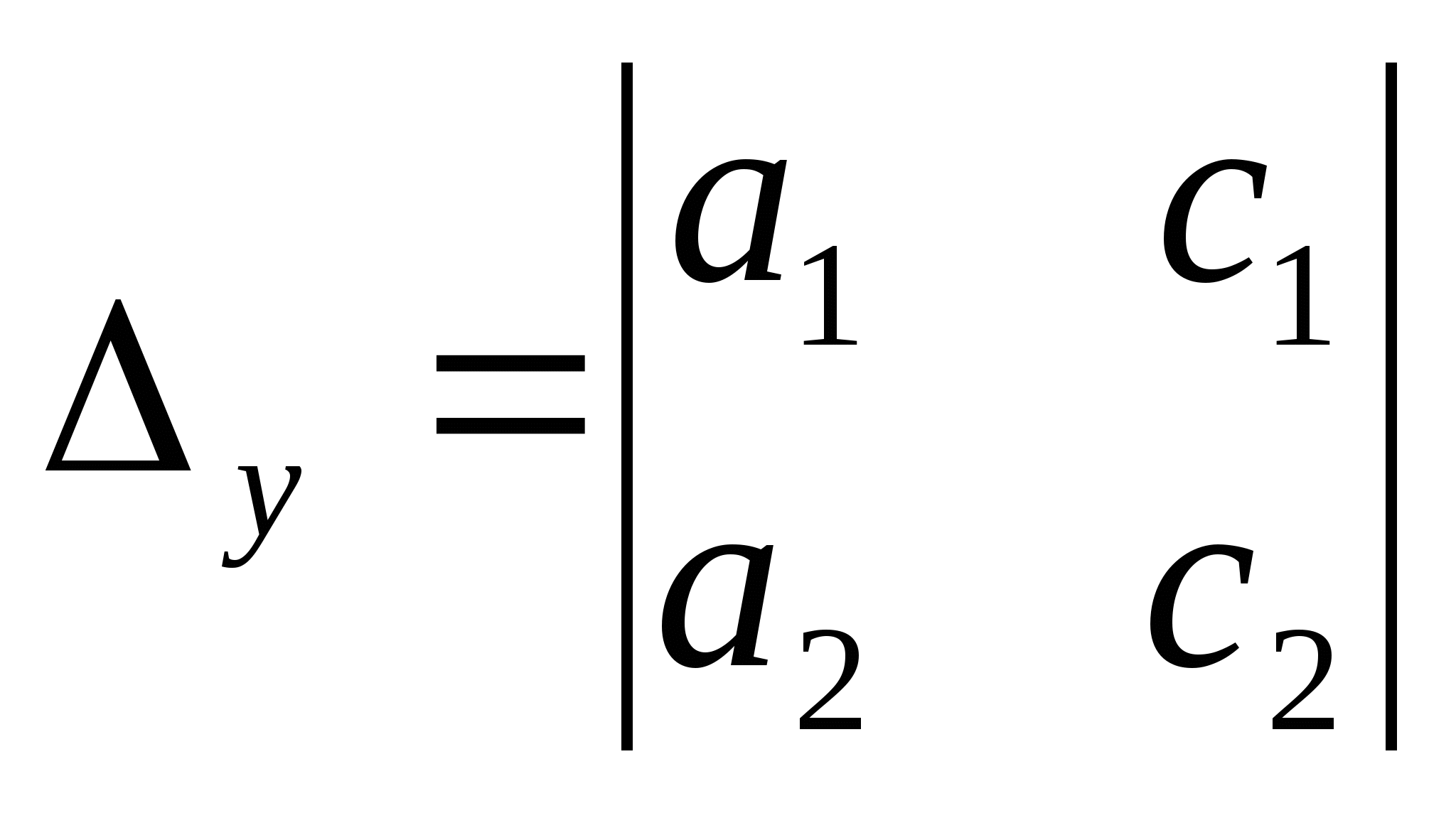
8.1. Вычислить определители:
1. ![]() 2.
2. ![]() 3.
3. ![]() 4.
4. ![]()
Решите системы уравнений разными способами:
8.2 ![]() 8.3
8.3 ![]() 8.4
8.4 ![]() 8.5
8.5 ![]()
8.6 ![]() 8.7
8.7 ![]() 8.8
8.8 ![]() 8.9
8.9![]()
8.10 ![]() 8.11
8.11![]() 8.12
8.12![]() 8.13
8.13![]()
8.14 ![]() 8.15
8.15![]() 8.16
8.16 ![]()
§9. Линейные функции
Помните: для построения прямой линии достаточно найти две точки.
9.1 Постройте графики функций:
1. ![]() 3.
3. ![]() 5.
5. ![]() 7.
7. ![]()
2.![]() 4.
4. ![]() 6.
6. ![]()
![]()
9.2 Вычислите координаты точки пересечения прямых:
1. ![]() и
и ![]()
2. ![]() и
и ![]()
9.3 При каком значении х значение у=-5, если у=2х-3
При каком значении х значение у=-3, если у=-2х+3![]()

| Автор | |
|---|---|
| Дата добавления | 13.05.2019 |
| Раздел | Алгебра |
| Подраздел | Самостоятельная работа |
| Просмотров | 1514 |
| Номер материала | 6219 |