Технологическая карта по математике 6 класс "Случайные события".
ТЕХНОЛОГИЧЕСКАЯ КАРТА УРОКА
| Сведения об авторе | |
| Фамилия, имя, отчество (полностью) | Рябинина Любовь Александровна |
| Район | Озинский |
| Место работы | МОУ «СОШ п.Модин» |
| Должность | Учитель математики |
| УМК | Мерзляк А.Г. Математика: 6 класс: Учебник для учащихся образовательных организаций / А.Г. Мерзляк, В.Б. Полонский, М.С. Якир. - М.: Вентана-Граф, 2016. |
| предмет | Математика |
| класс | 6 |
| Общая информация | |
| Тема урока | Случайные события. Вероятности случайных событий |
| Тип урока | Урок изучения нового |
| Цель, задачи (образовательные, развивающие, воспитательные) | Образовательная: сформировать понятие случайного события, вероятности случайного события, научить находить вероятность случайного события. Развивающая: развитие памяти, познавательных интересов, речи, логической мыслительной деятельности. Воспитательная: воспитание интереса к предмету, активности, настойчивости способствовать воспитанию сознательной дисциплины, сотрудничества, товарищеских отношений друг к другу, самостоятельности, ответственного отношения к учёбе. |
| Планируемые результаты | |
| формирование ответственного отношения к учению, готовности и способности, обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, |
| Знать определение случайного события, достоверного события, невозможного события. Иметь представление о вероятности случайного события. Уметь находить вероятность случайного события. |
| Регулятивные:
Познавательные:
Коммуникативные:
|
| Формы контроля и диагностики достижения результатов обучения | Графический диктант на тему "Сравнение дробей", |
Программно-техническое и дидактическое обеспечение | |
| Необходимое оборудование |
|
| Программное обеспечение | MS Office, стандартное программное обеспечение компьютеров |
| Дидактическое обеспечение | Учебник |
| ЭОРы | Презентация "Случайные события. Вероятности случайных событий" |
| № | Этап урока | Деятельность учителя | Деятельность ученика | Время | |
| 1 | Организационный. Мотивация к учебной деятельности. Цель этапа: включение учащихся в деятельность на личностно-значимом уровне. | Здравствуйте, ребята! Да, в жизни многое, несмотря на то, что мы всё планируем заранее, зависит от случая. Мир случайностей начинается сразу же за порогом нашего дома. Его Величество Случай, случайность — с ними мы встречаемся повседневно: землетрясения, ураганы, подъёмы и спады экономического развития, войны, болезни, случайная встреча, случайная находка или ошибка. Этот ряд можно продолжать бесконечно. Казалось бы, тут нет места для математики, — какие уж законы в царстве Случая! Но и здесь наука обнаружила интересные закономерности, которые позволяют человеку увереннее чувствовать себя при встрече со случайными событиями. | Приветствуют учителя. | 5 мин | |
| Ну что ж, друзья, давайте пойдём путём познаний. Но сначала мы вспомним сказочки. Муха по полю пошла, муха денежку нашла…. С какого события всё началось? Почему это событие случайно? | Пошла муха на базар и купила самовар. Со случайного. Муха нашла денежку. Потому что могло произойти или могло не произойти. |
| |||
| Молодцы. А вот следующая сказка . Какая это сказка? «Увидел Иван на земле перо Жар – птицы, да и поднял его. Предупреждал Конёк – Горбунок Ивана: Но для счастья своего, не бери себе его, Много, много непокою принесёт оно с собою. Так как вы думаете, от чего зависел весь ход сказки? - А чем закончилась сказка? К счастью, закончилось всё благополучно. Но случайности бывают не только в сказках. Обратите внимание на окно. Как вы думаете, пойдёт ли через 10 минут снег? -Мы делаем вывод: такое событие, снег, в данных условиях (декабрь,зима) через 10 минут может пойти, а может не пойти. - Как вы думаете, как называются такие события? -Запишите тему урока. «Случайные события. Вероятности случайных событий». | От случайного события, которое могло произойти, а могло и не произойти. Не послушался Иван, пришлось ему из – за этого случая много ходить по белу свету, а под конец даже нырять в кипяток. Случайные. | ||||
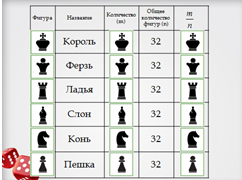
| 2 | Актуализация знаний Цель этапа: Повторение изученного материала, необходимого для «открытия нового знания», и выявление затруднений в индивидуальной деятельности каждого учащегося. | _ Как вы думаете, что это за игра? -На слайде изображены шахматные фигуры, как они называются. Сколько их? -Давайте определим, какую часть от всех фигур составляют короли? Фигуры «ферзь»? … -Как называются числа, записанные в пятом столбце? -Какие дроби мы получили, правильные или не правильные? Какие дроби называются правильными? -Приведите пример неправильной дроби. 2) -Сейчас мы с вами вспомним, как сравнивать обыкновенные дроби. Выполним графический диктант. Номер задания писать не нужно, только символ «>», «<» или «=» в одной строке. Проверим правильность выполнения задания. Посчитайте количество верных символов и запишите в оценочные листы. | Рассказывает об игре. Отвечает на вопрос. Отвечают на вопросы учителя. -Дроби. -Правильные. Отвечают на вопрос учителя. Отвечают на вопрос учителя. Выполняют задания в тетрадях. Заполняют оценочные листы. |
| 10 мин |
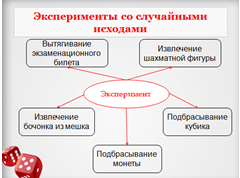
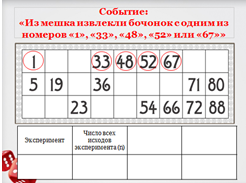
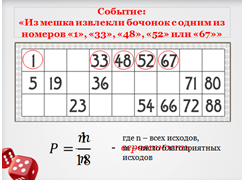
| 3 | Проблемное объяснение нового знания. Цель этапа: Обеспечение восприятия, осмысления и первичного закрепления учащимися, понятие вероятности случайного события | 1) -Поговорим еще об одной настольной игре – игре в лото. Расскажите, пожалуйста, об этой игре. -У меня в руках мешочек с бочонками лото, а на экране изображена одна из карточек. -Давайте проведем эксперимент. Я выну из мешка один бочонок. -Как вы думаете, можно ли угадать какой бочонок будет извлечен? -Каковы шансы, что мы угадаем? Итак, играем. -Возможно ли, что на первом ходе игры произойдет следующее событие: я извлеку из мешка «1»? -Насколько велики шансы выпадения «1»? -Возможно ли, что на первом ходе игры я достану бочонок с номером равным одному из чисел первой строки? -Насколько велики шансы, что это случиться? -Может ли произойти следующее событие: я достану бочонок с одним из номеров на карточке? -Насколько велики шансы, что это случиться? -Все три рассмотренные нами события можно назвать случайными, так как каждое из этих событий в одних и тех же условиях могло произойти, а могло и не произойти. -Попробуйте привести примеры других случайных событий. -Вернёмся к нашим событиям. Какое из трех событий наименее вероятное? -Какое из трех событий наиболее вероятное? -Выходит, что вероятности наступления случайных событий можно сравнивать. - Строгого определения понятия «вероятность» мы рассматривать не будем. - Что вы понимаете под словом «вероятность»? — Вот какое определение записано в толковом словаре Ожегова: Вероятность – возможность исполнения, осуществимости чего-нибудь. -Наука, которая занимается оценками вероятностей случайных событий, называется теорией вероятностей. -Теория вероятностей возникла в переписке двух великих учёных Блеза Паскаля и Пьера Ферма. -Итак, мы проводили эксперимент – извлекали бочонок из мешка, такой эксперимент называется экспериментом со случайными исходами, так как мы не можем точно знать какой бочонок мы достанем. Также экспериментами со случайными исходами можно назвать подбрасывание игрального кубика, вытягивание экзаменационного билета, извлечение наугад шахматной фигуры из коробки, подбрасывание монеты. -Сколько различных исходов всего в нашем эксперименте с лото? -Можно ли сказать, что вероятности всех исходов одинаковы? -Такие исходы называются равновероятными, а эксперимент – экспериментом с равновероятными случайными исходами. -Вернёмся к событию «Из мешка извлекли бочонок с номером равным одному из чисел первой строки», какие исходы должны быть у эксперимента, чтобы это событие наступило? -Эти исходы называются благоприятными. -Сколько исходов благоприятных событию? Какую часть благоприятные исходы составляют от числа всех возможных? -Это число и является вероятностью события. -Итак, как найти вероятность события с равновероятными исходами? -Найдем вероятности еще двух событий. -Какова вероятность, что из мешка я достану бочонок с номером 100? -События, вероятность которых равна нулю, называются невозможными. -Какова вероятность, что я достану бочонок с номером от 1 до 90? -События, вероятность которых равна 1, называются достоверными. -Какие события называются невозможными? Достоверными? | Рассказывает об игре. Отвечают на вопросы. -Возможно. - 1 шанс из 90. -Возможно. - 5 возможностей из 90. -Да. - 15 возможностей из 90. Приводят примеры. -Первое -Третье Отвечают на вопросы. -90 -Да. -Извлечем «1». -Извлечем «33». -Извлечем «48». -Извлечем «52». -Извлечем «67». -5 -1/18. -Нужно найти отношение числа благоприятных исходов к числу всех исходов. - 0 -1 Отвечают на вопросы учителя. |
| 10 мин |
| 4 | Физкультминутка | -Давайте немного разомнемся. И в этом тоже нам помогут настольные игры. Я буду подбрасывать игральный кубик. Будем выполнять упражнение столько раз, сколько точек выпадет на кубике. | Выполняют упражнения. |
| 2 мин |
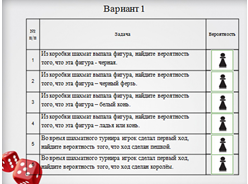
| 5 | Первичное закрепление нового знания. Цель этапа: закрепление нового знания; выявить пробелы первичного осмысления изученного материала, неверные представления учащихся; провести коррекцию. | 1) Потренируемся находить вероятности случайных событий. Вы будете работать в парах. На партах у вас лежат варианты с заданиями. Для каждого из 6 событий вы должны найти вероятности, и записать их в таблицу, а также ответить на предложенные вопросы. Договоритесь заранее, кто из вас будет отвечать, а кто фиксировать правильность выполнения задания. Опрашивает по одной паре из каждого варианта. -Посчитайте количество правильных ответов и запишите в оценочные листы. 2)-Вы все молодцы. Хорошо справились с заданием. Теперь поработаем с учебником и выполним № 809. Каждый выполняет задание индивидуально в своей тетради. Саша выполнит задание на доске. -Проверим, как вы справились с этим заданием. -Запишите количество верно выполненных заданий в оценочный лист. | Выполняют задание предложенного варианта. Участник одной пары отвечает, остальные фиксируют правильность выполнения заданий, вносят коррективы. Заполняют оценочный лист. Ученики выполняют задания в тетради. Один ученик выполняет задание на доске. Сверяют свои ответы с ответами на доске. Заполняют оценочный лист. |
| 15 мин |
| Согласитесь, ребята, случайности порой нам мешают, путают наши планы. Исключить их из жизни мы не можем, поэтому мы должны уметь их учитывать. Давайте попробуем это сделать. Мне нужен помощник . Глубокоуважаемый Помощник , переложите яблоки с этого блюда в корзину и прокомментируйте, сколько и какие это яблоки. | 5 красных и 2 жёлтых | ||||
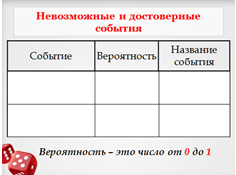
| 3) Давайте оценим следующие события: Помощник, вынимайте яблоко, не заглядывая в корзину. Событие А: вынуто красное яблоко. Событие В: вынуто желтое яблоко. Событие С: вынуто зеленое яблоко. Событие Д: вынуто яблоко. - Какие события будут случайными? - Верно. Помощник, а что вы можете сказать о событии В? - Да, наш помощник не волшебник! Как называются такие события? - Помощник, а как мы охарактеризуем событие Д? -Какое это событие? - Вы заметили, что всякий раз, характеризуя событие, я говорю: «при данных условиях», «при одних и тех же условиях». Как вы думаете, почему? - Что произойдёт с характеристиками наших событий, если в корзине жёлтые яблоки заменить зелёными? Возможность наступления событий зависит от условий, в которых оно происходит. - Давайте перейдём к следующей характеристике событий. Взять пакет и спросить: как вы думаете, у какого события больше шансов произойти: А или С? - Математики говорят в этом случае, что событие А более вероятно, а событие С менее вероятно. Я уравняю количество красных и зелёных яблок в корзине, вынув из корзины ещё одно яблоко. А теперь какое событие более вероятно: А или С? События, имеющие равные шансы наступления, называют равновероятностными. | Приглашённый вынимает яблоки, не заглядывая в пакет. События А и С – случайные, так как из пакета, не заглядывая в него, можно вынуть как красное яблоко, так и жёлтое. Это событие невозможное. События, которые при данных условиях не могут произойти, называют невозможными. - Так как в коробке только яблоки, то событие Д происходит каждый раз, когда мы вынимаем что – то из коробки. События, которые при данных условиях обязательно происходят, называются достоверными. - При изменении условий может измениться и возможность наступления события, его характеристика. Событие будет В случайным, а событие С невозможным. У события А, так как красных яблок в коробке больше. У этих событий равные шансы. |
| |||
| 6 | Рефлексивно оценочный этап. Цель этапа: Самоконтроль, обнаружение детьми своей компетентности или своих ошибок и затруднений, связанных с новым учебным материалом; оценка эффективности, исполненной ими деятельности. |
Охарактеризуйте следующие события как достоверные, невозможные, равномерные или случайные: 1. Сегодня будний день. (Достоверное) 2. Попугай научится говорить. (Случайное) 3. Мой день рождения — число, меньшее 32. (Достоверное) 4. Выпало чётное или нечётное количество очков. (Равновероятностное) 5. День рождения моего друга 30 февраля. (Невозможное) 6. Ель — вечнозелёное дерево. (Достоверное) 7. Завтра я стану космонавтом. (Невозможное) 8. Выпало число 6 или 7. (равновероятностное) 9. Сорванный цветок погибнет. (Достоверное) 10. Температура тела поднимется до 50 градусов. (Невозможное) 11. Осенью воробьи улетают на юг. (Невозможное) 12. Выпало одно очко или очков больше 3 (Равновероятностное)
Поднимите руки те, кто набрал 19 баллов и больше. Поднимите руки, кто набрал меньше 9 баллов. Соберите листы самоконтроля, я все проверю и выставлю вам оценки. -Сегодня вы научились элементарным способам подсчёта вероятностей, почувствовали, как проявляется вероятность. Вы видите, что бывает полезно знать и учитывать законы теории вероятностей. В жизни нужно поступать так, чтобы шансы на успех были наибольшими, случайное событие нельзя предугадать, но можно найти его вероятность. Моё пожелание – увереннее чувствуйте себя в незнакомых ситуациях, реально оценивайте свои шансы и возможный результат какого – либо вида деятельности. | Отвечают на вопросы. Заполняют оценочный лист. |
| 3 мин |
| 7 | Домашнее задание |
|

| Автор | |
|---|---|
| Дата добавления | 10.02.2019 |
| Раздел | Математика |
| Подраздел | Конспект урока |
| Просмотров | 2271 |
| Номер материала | 6108 |