
Урок "Алгебраические дроби. Основные понятия"

Краткое описание документа:
Видеоурок «Алгебраические дроби. Основные понятия» знакомит учеников с понятием алгебраической дроби, формирует умение решать примеры и задачи с алгебраическими дробями. Данное наглядное пособие повышает эффективность урока. Для этого используются инструменты, которые доступны при составлении видеоуроков – построение чертежей, включение иллюстраций, голосовые комментарии, анимационные эффекты. Такие инструменты помогают удержать внимание учеников на изучении материала. С помощью анимационных эффектов в ходе демонстрации учебный материал представляется более понятным и доступным. Чтобы улучшить запоминание теоретических основ, они представлены с выделением важных понятий цветом, формулировка определений дополнительно озвучивается.
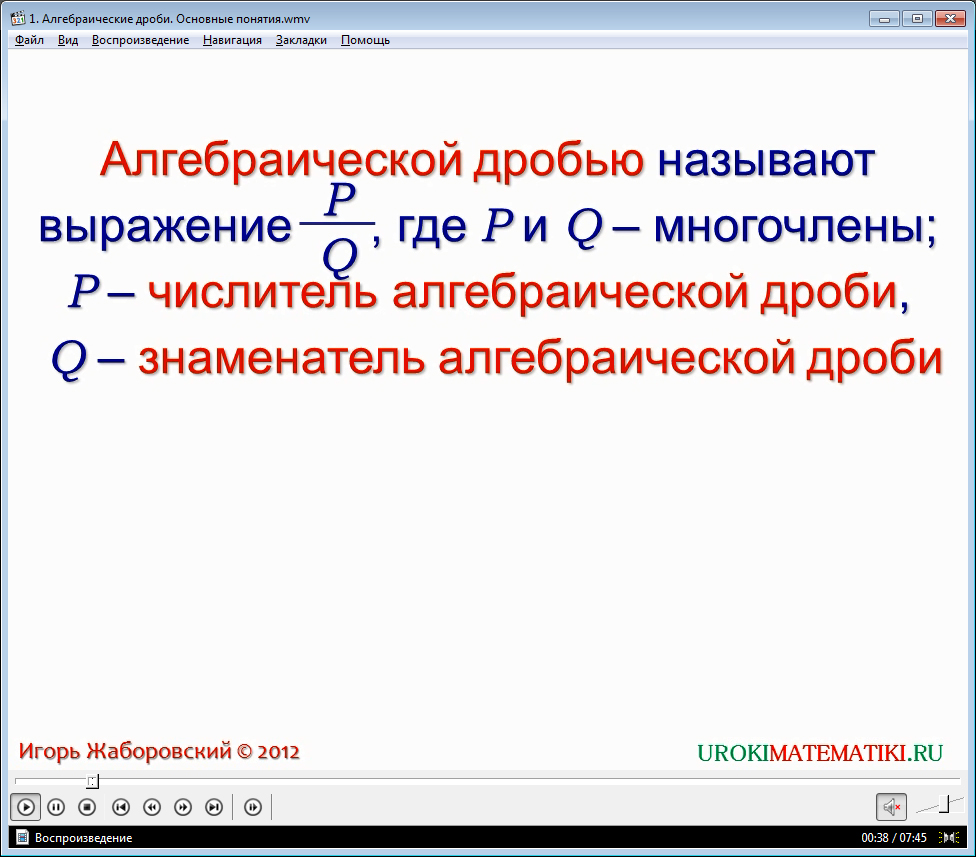
Демонстрация начинается с представления названия темы. Элементы теории алгебраических дробей уже знакомы ученикам из программы алгебры 7 класса. В данном разделе курса понятия знакомятся непосредственно с данной теорией, углубляется и обобщается понятие алгебраической дроби. Ученикам напоминается, когда они сталкивались с теорией алгебраических дробей, какие действия производили с дробями ранее. Далее дается определение алгебраической дроби как выражения P/Q, в котором P и Q являются многочленами. Напоминается, что алгебраическая дробь состоит из числителя P и знаменателя Q. Под определением даются примеры алгебраических дробей, в числителе и знаменателе которых стоят одночлены и многочлены. На примере представленных выражений отмечается, что как числителем, так и знаменателем дроби может быть одночлен или многочлен.
После представления определения и примеров указывается на возможность представить любой многочлен в виде дроби. Подобная возможность демонстрируется на примере многочлена 2х2+5х+3, который можно записать как дробь со знаменателем 1, то есть (2х2+5х+3)/1. Таким образом, многочлен является частным случаем алгебраической дроби. Также продемонстрировано разбиение алгебраической дроби, в числителе которой двучлен, на сумму двух дробей (3а+7)/5=3а/5+7/5. Отмечена возможность сокращения алгебраической дроби, аналогично сокращению обыкновенной дроби, на примере (а2-4)/(а+2)=а-2. Такое сокращение возможно после преобразования дроби, используя свойства алгебраических выражений. Все эти свойства изучались и при рассмотрении обыкновенных дробей, поэтому при их распространении на алгебраическую дробь, сложностей в освоении не возникает. Примером служит дробь 10/5, по сути представляющая число 2.
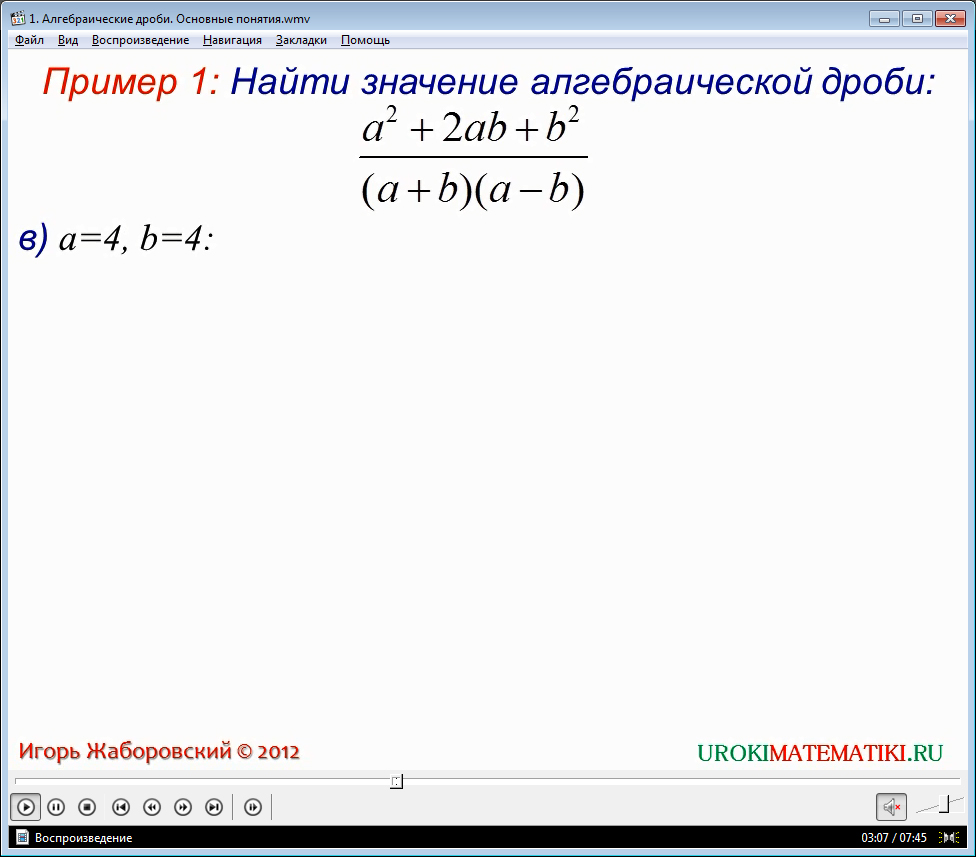
Далее с помощью рассмотрения примеров по данной теме, учитель продолжает формировать умение решать алгебраические дроби. В примере 1, решение которого описывается на экране, необходимо вычислить значение алгебраической дроби (а2+2ab+b2)/(a+b)(a-b). К данному выражению дается три пары значений a и b, после подстановки которых необходимо найти значение алгебраической дроби. Находится значение дроби при a=2, а b=1. Вычислив дробь, получаем ее значение 3. Аналогично вычисляется значение дроби при a=5, а b=0. Значение дроби при этом 1. Отмечается особенность вычислений во второй паре значений. При подстановке в выражение пары значений a=4 и b=4, в знаменателе дроби один множитель обращается в нуль. Это вызывает исключение, так как на нуль делить нельзя, поэтому данное выражение с такой парой значений не имеет смысла. Так вводится понятия допустимого и недопустимого значения переменной. Под примером формулируется определение допустимого значения переменной, входящей в состав алгебраической дроби. Отмечается, что это такое значение, которое не обращает в нуль знаменатель дроби. К примеру, решенному без использования возможности сокращения дроби, делается замечание. Отмечается, что подобная дробь решалась бы более просто, если бы перед постановкой значений переменных ее числитель и знаменатель бы были сокращены на выражение (a+b). Так как в числителе дроби находится выражение, которое, пользуясь формулами сокращенного умножения, можно представить в виде произведения (a+b)(a+b), а в знаменателе находится произведение (a+b)(a-b). После сокращения на выражение (a-b) в числителя и знаменателя, в итоге получается (a+b)/(a-b).

Далее описывается решение задачи, в которой необходимо найти скорость лодки, движущейся по реке, если скорость течения 2 км/ч, а лодка за 2 часа прошла 10 км по течению и 6 км против него. Наряду с представлением приемов решения алгебраических дробей, при демонстрации решения данной задачи учитель продолжает формировать у учеников умение составлять математические модели, использовать математический аппарат при решении задач. За х предлагается взять собственную скорость лодки, при этом, когда она движется по течению, ее скорость х+2, а против течения х-2. Тогда время, затраченное на путь по течению, находится по формуле 10/(х+2), а время на движение против течения 6/(х-2). Зная время, затраченное на весь путь, составляется уравнение 10/(х+2)+ 6/(х-2)=2. Замечено, что в выражении присутствуют алгебраические дроби, а также, что для решения подобных задач нужно уметь производить операции с алгебраическими дробями. На примере данной задачи подчеркивается важность умения оперировать алгебраическими дробями. Таким образом, стимулируется также мотивация к изучению теории алгебраических дробей на следующих уроках математики.

Видеоурок «Алгебраические дроби. Основные понятия» рекомендуется применять для повышения эффективности традиционного школьного урока математики. Пособие может сопровождать объяснение учителя в ходе дистанционного занятия по этой теме. Ученикам, недостаточно хорошо освоившим тему, видеоурок может быть рекомендованным для самостоятельной работы дома.
| Автор | |
|---|---|
| Дата добавления | 27.07.2014 |
| Раздел | Алгебра |
| Подраздел | Видеоурок |
| Просмотров | 9656 |
| Номер материала | 524 |